GIZEH - GEODÄTISCHE ERKENNTNISSE
Copyright © Klaus Piontzik
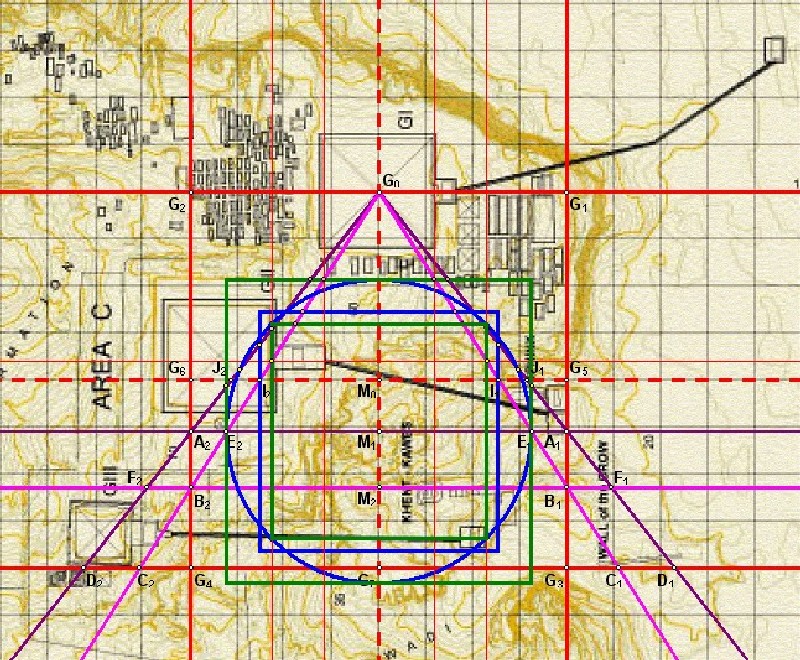
| Die Schenkel des 7:11
Winkels schneiden die Waagerechte
A1M1A2,
also die Hauptachse von Quadratur 1.1,
in den Punkten E1
und E2. Die Quadratur 1.2 wird durch das Quadraturdreieck G0E1E2 gebildet, mit dem 7:11 Verhältnis |

| Abbildung 9a.1 - Die Quadratur 1.2 in der Karte von Mark Lehner |
| Bezüge
zu architektonischen Teilen: Das Inquadrat der Quadratur 1.2 ergibt die Ostseite der Chefren-Pyramide Dabei liegt der Schnittpunt des 7:11 Schenkel und dem Inquadrat auf der Ostseite der Chefren-Pyramide Das Inquadrat und das Umquadrat der Quadratur 1.2 definieren die Postion des Taltempels des Mykerinos |
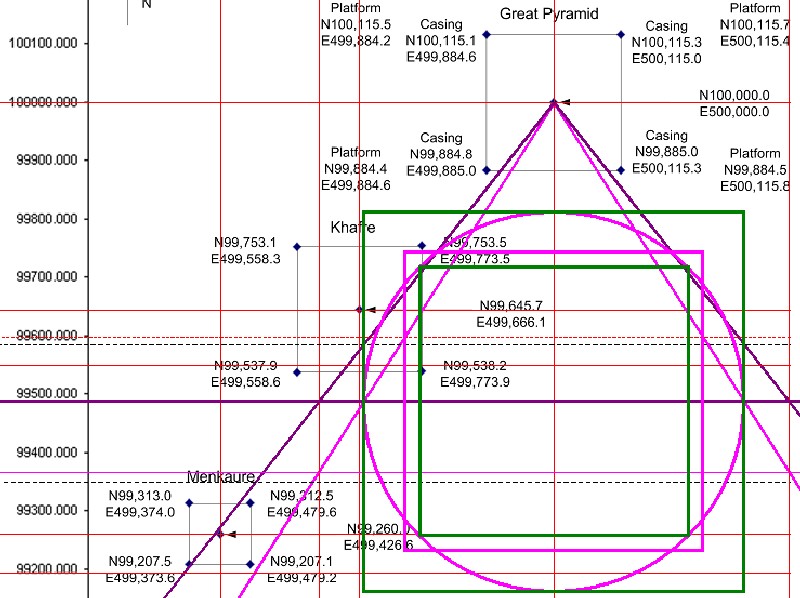
| Abbildung 9a.2 - Die Quadratur 1.2 in der Karte von Glen Dash |
| Es ergeben sich wieder Schnittpunkte zwischen den 7:11 und 11:14 Schenkeln mit der Quadraturkonstruktion 1.2 |
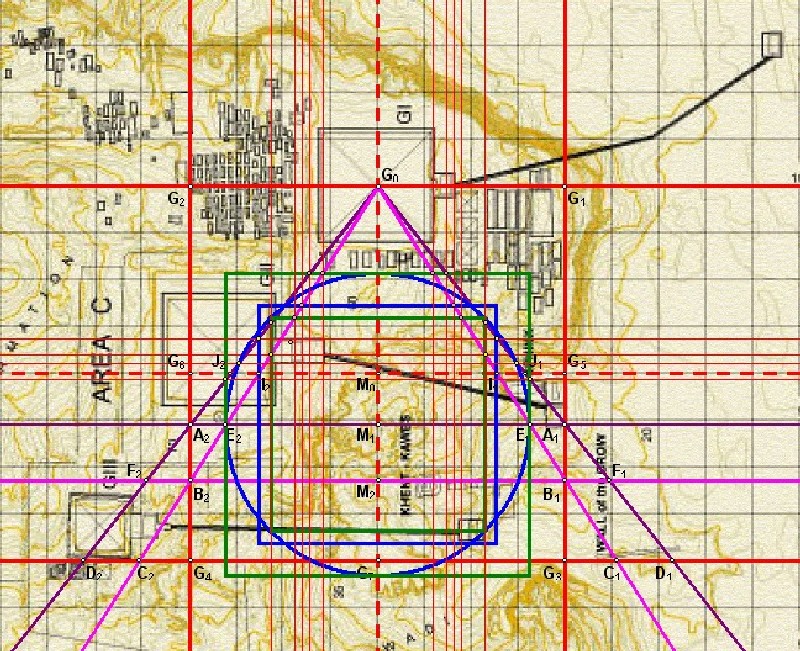
| Abbildung 9a.3 - Die Quadradur 1.2 und alle Schnittpunkte |
| Es ergeben sich Bezüge zum Tempel des Chefren, dem Taltempel des Mykerinos und dem Grab des Chentkaues. |
| Aus der Menge aller Schnittpunkte und Waagerechten aus der Quadratur 1.2 werden nur die eingezeichnet, die eine Beziehung zu den Tempeln haben. Und zwar zum Taltempel des Mykerinos sowie dem Tempel des Chefren. |
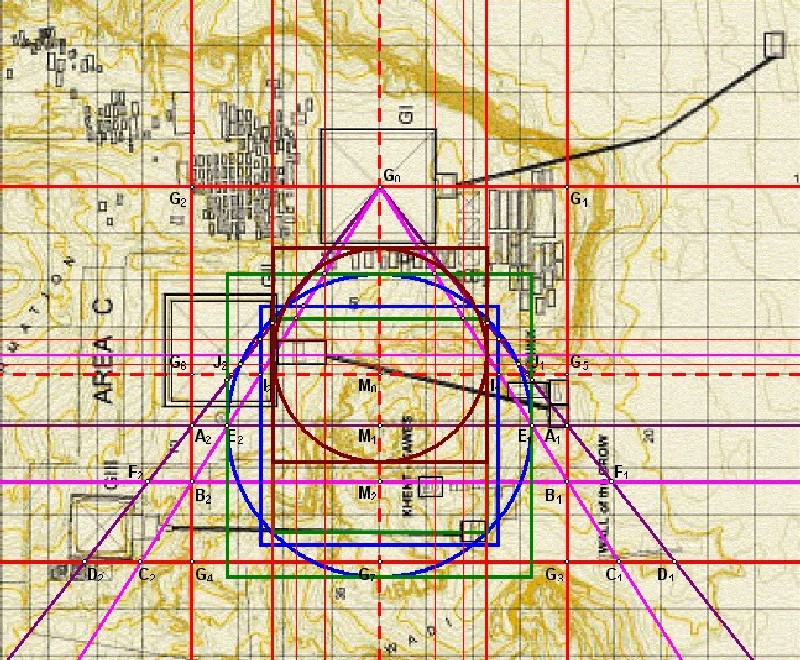
| Abbildung 9a.4 - Tempel |
| Die Schnittpunkte des 7:11
Schenkels mit dem Inquadrat ergeben
mit G0 das Quadraturdreieck
5 mit der Qudraturkonstruktion 5.
Der dazu gehörige Quadraturkreis 5 und dessen Umquadrat sind in Abbildung 9a.4 in dunkelrot eingezeichnet. |