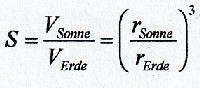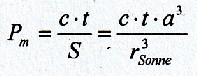GIZEH - GEODÄTISCHE ERKENNTNISSE

5 - Bestimmung des Basisumfanges der grossen Pyramide

5.1 - Ein erster Ansatz

In diesem Kapitel soll nun eine Bestimmung des Baisumfanges erfolgen. Und zwar auf eine Art und Weise, wie sie im naturwissenschaftlichen Bereich üblich ist, wenn aus vorhandenen Meßwerten eine Gesetzmäßigkeit abgeleitet werden soll.

Alle bisherigen Berechnungen des Pyramidenumfanges beziehen lediglich den Äquatorumfang mit ein. Da die Erde keine Kugel ist, existiert aber nicht nur ein Durchmesser. In erster Näherung läßt sich die Erdgestalt durch eine Ellipse darstellen, die um ihre kleine Achse, also die Polachse rotiert. Solch ein Rotationsellipsoid wird auch Sphäroid genannt.

Da Pol- und Äquatorradius voneinander unterschiedlich sind, werden in den folgenden Rechnungen natürlich auch beide verwendet. Dabei ist a die große Halbachse bzw. der Äquatorradius, b ist die kleine Halbachse bzw. der Polradius.

Modelle der Erde, die Sphäroide als Grundlage verwenden, heißen geodätische Systeme, und sind im vorherigen Kapitel ja eingehend erläutert worden. Da im Laufe der Zeit verschiedene geodätische Systeme benutzt worden sind, wird hier nicht nur eines, sondern gleich mehrere von ihnen verwendet. Dies hat den Zweck bessere Vergleichsmöglichkeiten zu erhalten, und dadurch Grenzen besser bestimmen zu können. Daher noch einmal eine kleine Übersicht der Werte, für die Systeme, die hier benutzt werden.

Jahr der Einführung	Geodätisches System	Pol Durchmesser in Meter	Äquator Durchmesser in Meter	Numerus der Abplattung
		2b	2a	n

1830	Airy	12712513,82	12755126,79	299,3249646
1830	Everest	12712150,83	12754552,69	300,8017
1841	Bessel	12712157,93	12754794,31	299,1528128
1866	Clarke	12713167,60	12756412,8	294,9786982
1880	Clarke	12713029,74	12756498,29	293,465
1909	Hayford (IRE)	12713823,89	12756776	297
1942	Krassowski	12713726,04	12756490	298,3
1956	Hough	12713588,69	12756540	297
1960	Fischer	12713568,57	12756332	298,3
1960	WGS	12713566,57	12756330	298,3
1961	WGS	12713554,74	12756326,76	298,24
1966	WGS	12713519,54	12756290	298,25
1967	IUGG	12713550,00	12756320	298,25
1967	GRS	12713549,03	12756320	298,247167427
1968	Fischer	12713536,67	12756300	298,3
1969	SüdAm.	12713549,44	12756320	298,25
1972	WGS	12713501,04	12756270	298,26
1975	GRS	12713510,58	12756280	298,257
1976	SAO/GRIM2	12713540,19	12756310	298,255
1977	Enz. Brit.	12713553,42	12756360	298
1980	GRS	12713504,63	12756274	298,257222101
1984	WGS	12713504,63	12756274	298,257223563

Tabelle 5.1

Wenn die große Pyramide in Relation zu Erddaten steht, ist es durchaus sinnvoll die Umfänge bzw. Achsen der Erde zu gebrauchen. Ein erster allgemeiner Ansatz um den Basisumfang U_B der großen Pyramide von Gizeh zu erhalten, besteht dann darin, den (entsprechenden) Erdumfang U durch einen bestimmten Faktor k zu teilen. Mathematisch, also durch eine Gleichung ausgedrückt:

U_A ist der Äquatorumfang mit U_A = 2·a·pi
U_P ist der Umfang der Erde, über die Pole gemessen, mit U_P = 2·b·pi

Genau genommen ist der Umfang über die Pole ein Ellipsenumfang mit U_E = 2·a·pi ·gamma
gamma ist dabei ein Umfangsfaktor, der abhängig von den Achsen ist U_E= 2·b·pi ·gamma ·f^-1

Dieser Ellipsenumfang wird in die Betrachtung mit einbezogen, und als Gleichung läßt sich das in Übereinstimmung mit der bisherigen Ausdrucksweise so formulieren:

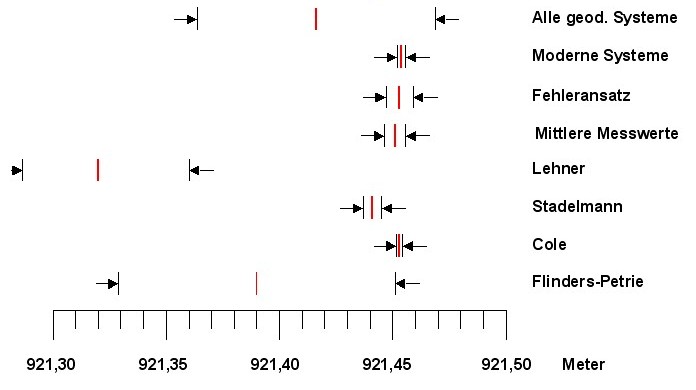
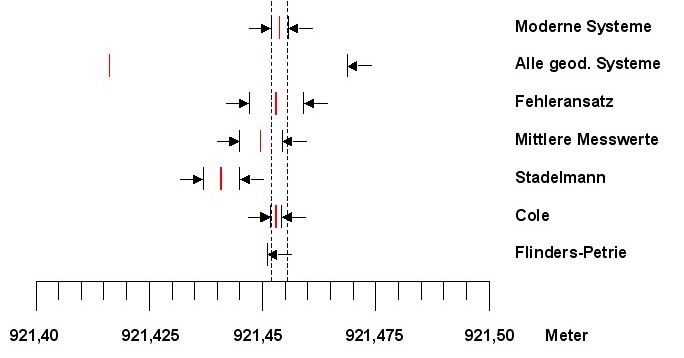
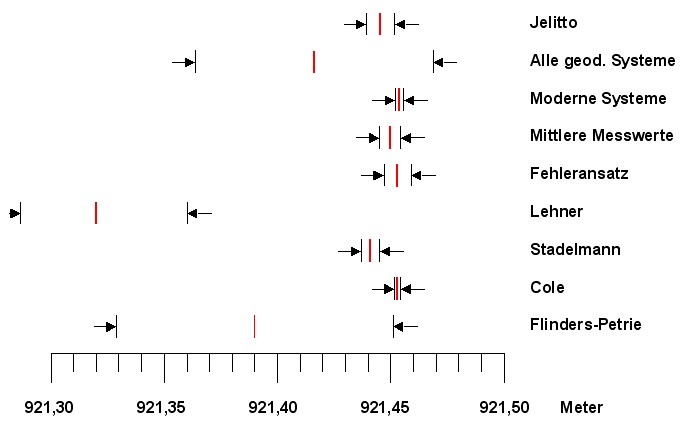
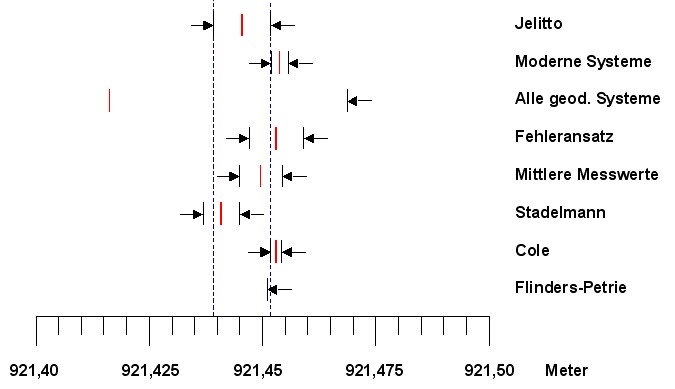
Der Fehleransatz aus Kapitel 4 ergab für den Basisumfang der großen Pyramide, den von Cole gemessenen Wert, versehen mit erweiterten Fehlergrenzen:

U_B : 921,453072 m ± 0,006 m

921,447 m < U_B < 921,459 m

Mit den Achsen-Werten der geodätischen Systeme und dem gemessenen Umfang läßt sich eine erste quantitative Bestimmung des Faktors k durchführen. Die oben aufgestellten Gleichungen für den Basisumfang brauchen nur nach k umgestellt zu werden:

Und durch Einsetzen der Werte aus den geodätischen Systemen und dem gemessenen Basisumfang in die Gleichungen für den Faktor k ergibt sich:

Jahr der Einführung	Geodätisches System	k_P	k_A	k_E

1830	Airy	43341,91424	43487,19847	43414,58674
1830	Everest	43340,67667	43485,24114	43412,98899
1841	Bessel	43340,70088	43486,06491	43413,41331
1866	Clarke	43344,14323	43491,58298	43417,89440
1880	Clarke	43343,67322	43491,87444	43417,80545
1909	Hayford (IRE)	43346,38078	43492,82127	43419,63189
1942	Krassowski	43346,04717	43491,84618	43418,97728
1956	Hough	43345,57889	43492,01665	43418,82864
1960	Fischer	43345,51030	43491,30750	43418,43950
1960	WGS	43345,50348	43491,30068	43418,43268
1961	WGS	43345,46314	43491,28963	43418,40700
1966	WGS	43345,34313	43491,16430	43418,28433
1967	IUGG	43345,44698	43491,26658	43418,38739
1967	GRS	43345,44368	43491,26658	43418,38574
1968	Fischer	43345,40154	43491,19840	43418,33057
1969	SüdAm.	43345,44508	43491,26658	43418,38644
1972	WGS	43345,28006	43491,09611	43418,21869
1975	GRS	43345,31259	43491,13021	43418,25200
1976	SAO/GRIM2	43345,41354	43491,23249	43418,35362
1977	Enz. Brit.	43345,45864	43491,40296	43418,46146
1980	GRS	43345,29230	43491,10975	43418,23163
1984	WGS	43345,29230	43491,10975	43418,23163

Tabelle 5.2

Aus dieser Tabelle läßt sich eine erste Eingrenzung für k erstellen:

43340 < k_P < 43347

43485 < k_A < 43493

43412 < k_E < 43420

Wie zu sehen ist, liegt der Faktor k tatsächlich in der Nähe der Zahl 43200. Als Konstruktionsvorschrift für den Umfang der großen Pyramide von Gizeh wird ja immer wieder folgende Rechnung angegeben: Man nehme den Umfang der Erde und teile ihn durch 43200.

Schränkt man die Betrachtung auf die moderneren Systeme ab 1961 ein, dann lassen sich die Grenzen sogar noch etwas einengen:

43345 < k_P < 43346	43491 < k_A < 43492	43418 < k_E < 43419

Schränkt man die Betrachtung noch weiter ein, indem man den Wert aus der Enzyklopedia Britannica entfernt, dann ergeben sich folgende minimale Grenzen:

43345,28 < k_P < 43345,46	43491,09 < k_A < 43491,26	43418,21 < k_E < 43418,38

Die Zahl 43200 wird oft als Zeitfaktor (1/2 Tag = 43200 Sekunden) interpretiert. Wie aber schon in der Einleitung erörtert, wird hier davon abgesehen, da keinerlei Hinweise vorhanden sind, die dieses unterstützen könnten.

Logischer ist, von der normalen Kreisteilung in Grad, Minuten und Sekunden auszugehen.
Ein Kreis besteht aus 360 Grad, wobei jedes Grad 60 Minuten enthält, und jede Minute wiederum 60 Sekunden besitzt. Insgesamt verfügt ein Kreis also über 360·60² = 1.296.000 Bogensekunden.

Um auf den Wert 43200 zu gelangen, muß durch 30 geteilt werden. Das heißt, bei dieser Art der Interpretation würde es sich um einen rein geometrischen Winkel von 30 Bogensekunden handeln.
Da in der Bestimmungsgleichung für den Basisumfang der Term 2·pi erscheint, ließe sich der Winkel sogar in Bogenmaß darstellen.

5.2 - Verfeinerung des Ansatzes

Für einen verfeinerten Ansatz kann man nun folgendermaßen vorgehen: Als Näherungswert wird 43200 angesetzt, und der Faktor k wird von jetzt ab sozusagen als Korrekturfaktor für den Wert 43200 betrachtet. Dieser Ansatz sieht dann so aus:

Die einzelnen Gleichungen werden wieder jeweils nach k umgestellt :

Durch Einsetzen der Werte aus den geodätischen Systemen und dem gemessenen Wert für den Basisumfang in die Gleichungen für den Faktor k erhält man dann folgende Tabelle:

Jahr der Einführung	Geodätisches System	k_P	k_A	k_E

1830	Airy	1,003285052	1,006648113	1,004967286
1830	Everest	1,003256404	1,006602804	1,004930301
1841	Bessel	1,003256965	1,006621873	1,004940123
1866	Clarke	1,003336649	1,006749606	1,005043852
1880	Clarke	1,003325769	1,006756353	1,005041793
1909	Hayford (IRE)	1,003388444	1,006778270	1,005084072
1942	Krassowski	1,003380722	1,006755699	1,005068918
1956	Hough	1,003369882	1,006759645	1,005065478
1960	Fischer	1,003368294	1,006743229	1,005056470
1960	WGS	1,003368136	1,006743071	1,005056312
1961	WGS	1,003367202	1,006742816	1,005055718
1966	WGS	1,003364424	1,006739914	1,005052878
1967	IUGG	1,003366828	1,006742282	1,005055264
1967	GRS	1,003366752	1,006742282	1,005055225
1968	Fischer	1,003365776	1,006740704	1,005053948
1969	SüdAm.	1,003366784	1,006742282	1,005055242
1972	WGS	1,003362964	1,006738336	1,005051359
1975	GRS	1,003363717	1,006739125	1,005052130
1976	SAO/GRIM2	1,003366054	1,006741493	1,005054482
1977	Enz. Brit.	1,003367098	1,006745439	1,005056978
1980	GRS	1,003363248	1,006738652	1,005051658
1984	WGS	1,003363248	1,006738652	1,005051658

Tabelle 5.3

Aus der Tabelle 5.3 lassen sich die maximalen Grenzen der k-Faktoren ableiten:

1,00325 < k_P < 1,00339

1,00660 < k_A < 1,00678

1,00493 < k_E < 1,00509

Schränkt man auch hier die Betrachtung auf die moderneren Systeme ab 1961 ein, dann lassen sich die Grenzen sogar noch etwas einengen:

1,003364 < k_P < 1,003368

1,006738 < k_A < 1,006746

1,005051 < k_E < 1,005057

Wird (wie leider allgemein üblich) der Faktor k gleich 1 gesetzt, so erhält man, (bei weiterer Rechnung mit dem Äquatorradius), etwa den von Fix errechneten Wert für den Sockelumfang.

Über den Basisumfang ist damit aber noch nichts ausgesagt. Die nahe 1 liegende Größe für den Korrekturfaktor k scheinen den meisten Pyramidenforschern nichts zu sagen. Hat man sich jedoch ein wenig mit Ellipsenmathematik bzw. geodätischen Systemen beschäftigt, so kommt einem diese Faktorgröße irgendwie bekannt vor !

5.3 - Quantisierung des Ansatzes

Vergleicht man nämlich mit den Parametern aus den geodätischen Systemen, so ist nun relativ einfach zu zeigen, dass k_P etwa in der Größe des Kehrwertes des Formfaktors f_o liegt. Bei k_A handelt es sich etwa um das Quadrat des Kehrwertes des Formfaktors f_o. Hier die Werte für die Terme des Formfaktor :

Jahr der Einführung	Geodätisches System

1830	Airy	1,003352049	1,006715334
1830	Everest	1,003335538	1,006682201
1841	Bessel	1,003353984	1,006719218
1866	Clarke	1,003401607	1,006814785
1880	Clarke	1,003419212	1,006850116
1909	Hayford (IRE)	1,003378379	1,006768171
1942	Krassowski	1,003363606	1,006738525
1956	Hough	1,003378378	1,006768170
1960	Fischer	1,003363606	1,006738525
1960	WGS	1,003363606	1,006738526
1961	WGS	1,003364285	1,006739888
1966	WGS	1,003364171	1,006739661
1967	IUGG	1,003364127	1,006739572
1967	GRS	1,003364204	1,006739725
1968	Fischer	1,003363606	1,006738526
1969	SüdAm.	1,003364171	1,006739661
1972	WGS	1,003364058	1,006739434
1975	GRS	1,003364092	1,006739501
1976	SAO/GRIM2	1,003364115	1,006739547
1977	Enz. Brit.	1,003367004	1,006745344
1980	GRS	1,003364090	1,006739497
1984	WGS	1,003364090	1,006739497

Tabelle 5.4

Bildet man aus der Tabelle 5.4 die maximalen Intervalle, so erhält man:

1,003353 <

< 1,003419

1,006719 <

< 1,006850

Bildet man aus der Tabelle die Intervalle mit den Werten aus den moderneren Systemen ab 1961, so erhält man:

1,003363 <

< 1,003367

1,006738 <

< 1,006746

Hier noch mal die Grenzen der k-Faktoren aus dem verfeinerten Ansatz: für die moderneren Systeme ab 1961:

1,003364 < k_P < 1,003368

1,006738 < k_A < 1,006746

Durch Vergeich läßt sich eine sehr gute Übereinstimmung zwischen den k_P und k_A Faktoren und dem Formfaktor f_o sowie deren Intervalle verzeichnen.

Damit lassen sich jetzt folgende Relationen für die Korrekturfaktoren aufstellen:

5.4 - Basisumfang der großen Pyramide

Mit den abgeleiteten Relationen lassen sich die Gleichungen für den Basisumfang der großen Pyramide nun folgendermaßen angeben:

Einsetzten der Werte aus den geodätischen Systemen in die Gleichung G1 liefert dann folgende Werte für den Basisumfang:

Jahr der Einführung	Geodätisches System	U_B-GeoSys

1830	Airy	921,3915435
1830	Everest	921,3803966
1841	Bessel	921,3639717
1866	Clarke	921,3934191
1880	Clarke	921,3672615
1909	Hayford (IRE)	921,4623156
1942	Krassowski	921,4687907
1956	Hough	921,4452694
1960	Fischer	921,4573776
1960	WGS	921,4572322
1961	WGS	921,4557514
1966	WGS	921,4533043
1967	IUGG	921,4555526
1967	GRS	921,4554120
1968	Fischer	921,4550650
1969	SüdAm.	921,4554714
1972	WGS	921,4520673
1975	GRS	921,4527278
1976	SAO/GRIM2	921,4548529
1977	Enz. Brit.	921,4531589
1980	GRS	921,4522987
1984	WGS	921,4522987

Tabelle 5.5

Bildet man aus der Tabelle 5.5 das maximale Intervall mit dem geodätischen Basisumfang, so erhält man:

921,3639 m < U_B-GeoSys < 921,4687 m

Einschränkung des Intervalles auf die modernen Systeme ab 1961 liefert:

921,4520 m < U_B-GeoSys < 921,4557 m

Daraus ergibt sich der mittlere geodätische Basisumfang:

U_B : 921,45385 m ± 0,00185 m

Daraus ergibt sich der mittlere geodätische Pyramidenseite:

P : 230,3634 m ± 0,00046 m

230,36294 m < P_GeoSys < 230,36386 m

5.5 - Vergleich mit den Messwerten

Der Vergleich mit den mittleren Messwerten (Kapitel 4.1.5)

U_B : 921,449645 m ± 0,004645 m	921,445 m < U_B < 921,45429 m
P : 230,36241 m ± 0,00116 m	230,36125 m < P < 230,36357 m

Die Abweichung der Mittelwerte für den Basisumfang liegt bei 4,2 mm, und die Fehlergrenzen liegen damit knapp unterhalb der vorgegebenen minimalen geodätischen Fehlergrenze, wenn man sich auf die modernen Systeme beschränkt. Die Abweichung der Mittelwerte für die Pyramidenseite liegt bei 0,53 mm

Der Vergleich mit den Werten aus dem Fehleransatz:(Kapitel 4.2.4)

U_B : 921,45307 m ± 0,006 m	921,447 m < U_B < 921,459 m
P : 230,36326 m ± 0,0015 m	230,36176 m < P < 230,36476 m

Trägt man alle Intervalle graphisch über dem Baisumfang auf, ergibt sich die folgende Abbildung. Die Auflösung beträt 1 Teilstrich = 0,01 m

Abbildung 5.1 - Vergleich für den Basisumfang der großen Pyramide

Verfeinert man die Auflösung ergibt sich folgendes Bild. Die Auflösung beträt 1 Teilstrich = 0,005 m

Abbildung 5.2- Verfeinerter Vergleich für den Basisumfang der großen Pyramide

Wie zu sehen ist, stimmt der Fehleransatz, also der gemessene Wert von Cole und der geodätische Basisumfang ziemlich gut überein. Die Abweichung der Mittelwerte iegt lediglich bei etwa 0,778 mm, und damit innerhalb der vorgegebenen maximalen Fehlergrenze, wenn man sich auf die modernen Systeme beschränkt.Die Abweichung der Mittelwerte für die Pyramidenseite liegt bei 0,14 mm.

Der Basisumfang der großen Pyramide von Gizeh läßt sich mit hinreichender Genauigkeit aus den Daten der modernen geodätischen Systeme ableiten (G1 und G2).

5.6 - Resultat

Der Formfaktor f_o ist definiert als: f_o= b/a

Einsetzen in die obigen Gleichungen G1 und G2, liefert eine einzige Gleichung. Und zwar:

Für die Radien der Schmiegekreise einer Ellipse gelten die folgenden Beziehungen. r₁ ist dabei der Radius des kleineren Schmiegekreises, r₂ entspricht dem größeren Schmiegekreis

Damit läßt sich die End-Gleichung für den Basisumfang auch so formulieren:

Das bedeutet also, dass der Basisumfang der großen Pyramide nur sekundär auf die Achsen der Erdellipse bezogen sind, primär aber auf den kleinen Schmiegekreis.

Dies ist durchaus sinnvoll, da dieser kleinere Radius auch als Parameter zur Beschreibung von Ellipsen in der Kegelschnittform benutzt wird. Es gilt ja: r₁ = p

5.7 - Die Pyramidenseite nach Hans Jelitto

Hans Jelitto veröffentlichte 1999 das Buch "Pyramiden und Planeten" in dem er den Basisumfang der großen Pyramide aus dem Volumenverhältnis Sonne/Erde und der Lichtgeschwindigkeit ableitet.

5.7.1 - Voraussetzungen

Die Lichtgeschwindigkeit wird wie folgt angegeben: 299.792.458 m/s ± 1 m/s

Der Radius der Erde wird den geodätischen Systemen entnommen. Siehe Tabelle 5.1.

Auch der Sonnenradius ist inzwischen recht gut bekannt, da er für astronomische Berechnungen benötigt wird. (Wikipedia):

R_Sonne = 696342 Km ± 65 Km

Daraus ergeben sich folgende Grenzen für den Sonnenradius:

R_Max = 696407 Km
R_Min = 696277 Km

Das Volumenverhältnis Sonne/Erde ergibt sich zu:

Volumenverhältnis Sonne/Erde

Dabei gilt r_Erde = a = Äquatorradius (Siehe Tabelle 5.1)

Die Pyramideseite ergibt sich aus dem Lichtweg in einer Sekunde geteilt durch das Volumenverhältnis:

Pyramideseite

5.7.2 - Basisumfang

Einsetzen aller Faktoren in die Gleichungen liefert folgende Werte für den Basisumfang der großen Pyramide:

R_Min = 696277 Km ==> U_B = 921,7562 - 921,7676 m
R_Max = 696407 Km ==> U_B = 921,2401 - 921,2515 m

Insgesamt ergibt sich damit: U_B = 921,2401 - 921,7562 m

Der gemessene Basisumfang liegt zwar innerhalb des ermittelten Intervalls. Das Intervall selber aber umfasst 0,51 m, was viel zu groß für einen aussagekräftigen Ansatz ist.

5.7.3 - Sonnenradius

Mit dem gemessenen Basisumfang und den bestehenden Daten lässt sich eine Rückrechnung für den Sonnenradius tätigen, damit dieser das Intervall für den Basisumfang einhält.

R_Sonne = 696354,1 Km ± 4 Km

Nur wenn der Sonneradius innerhalb der angegebenen Grenzen von maximal 4 Km liegt funktioniert die Theorie von Jelitto bzgl. der Pyramidenseite der großen Pyramide.

5.7.4 - Pyramidenseite

Aus dem Sonnenradius ergibt sich für den Basisumfang:

U_B = 921,4490 - 921,4615 m

Der mittlere Basisumfang ergibt sich zu:

U_B : 921,4455 m ± 0,00625 m

921,43925 m < U_B < 921,45175 m

Die mittlere Pyramidenseite beträgt dann:

P : 230,3613 m ± 0,001562 m

230,359738 m < P < 230,362862 m

5.8 - Vergleich der Jelitto Daten

Der Vergleich mit den mittleren Messwerten (Kapitel 4.1.5)

U_B : 921,449645 m ± 0,004645 m	921,445 m < U_B < 921,45429 m
P : 230,36241 m ± 0,00116 m	230,36125 m < P < 230,36357 m

Die Abweichung der Mittelwerte für den Basisunfang liegt bei 4,145 mm, und die Fehlerintervalle überlappen sich. Die Abweichung der Mittelwerte für die Pyramidenseite liegt bei 1,11 mm

Der Vergleich mit den Werten aus dem Fehleransatz:(Kapitel 4.2.4)

U_B : 921,45307 m ± 0,006 m	921,447 m < U_B < 921,459 m
P : 230,36326 m ± 0,0015 m	230,36176 m < P < 230,36476 m

Die Abweichung der Mittelwerte iegt bei 7,57 mm, und die Fehlerintervalle überlappen sich. Die Abweichung der Mittelwerte für die Pyramidenseite liegt bei 1,96 mm

Der Vergleich mit den geodätichen Messwerten (Kapitel 5.4)

U_B : 921,45385 m ± 0,00185 m	921,4520 m < U_B < 921,4557 m
P : 230,3634 m ± 0,00046 m	230,36294 m < P < 230,36386 m

Die Abweichung der Mittelwerte iegt lediglich bei etwa 8,35 mm, und die Fehlerintervalle überlappen sich. Die Abweichung der Mittelwerte für die Pyramidenseite liegt bei 2,1 mm

Trägt man alle Intervalle graphisch über dem Baisumfang auf, ergibt sich folgende Abbildung: Die Auflösung beträt 1 Teilstrich = 0,01 m

Abbildung 5.3 - Vergleich für den Basisumfang der großen Pyramide

Verfeinert man die Auflösung ergibt sich folgendes Bild. Die Auflösung beträt 1 Teilstrich = 0,005 m

Abbildung 5.4 - Verfeinerter Vergleich für den Basisumfang der großen Pyramide

Das Jelitto Intervall und das Intervall der mittleren Messwerte (Kapitel 4.1.5) überlappen. sich. Der Jelitto Mittelwert liegt an der unteren Grenze des Messwert Intervalles. Die Mittelwerte liegen 4,145 mm außeinander.

Das Jelitto Intervall und das Intervall des Fehleransatzes (Kapitel 4.2.4) überlappen sich zwar noch, aber die Mittelwerte liegen 7,57 mm außeinander.

Das Jelitto Intervall liegt unterhalb des geodätischen Intervalles. Die Mittelwerte liegen 8,35 mm außeinander.

Zum Vergleich

Die Abweichung der Mittelwerte für das geodätische Intervall und das Intervall der mittleren Messwerte für den Basisumfang liegt bei 4,2 mm,

Die Abweichung der Mittelwerte für das geodätische Intervall und dem Fehleransatz liegt bei etwa 0,778 mm

Hieraus wird ersichtlich das der Mittelwert des Jeltto Ansatzes bzgl. der geodätischen Daten etwas zu klein geraten ist. Der Unterschied Jelitto Ansatz zum geodätischen Ansatz beträgt 8,35 mm.

Seite: 0 1 2 3 4 5 6 7 a 8 a 9 a 10 a 11 a 12 a 13 a 14