GIZEH - GEODÄTISCHE ERKENNTNISSE
Copyright © Klaus Piontzik
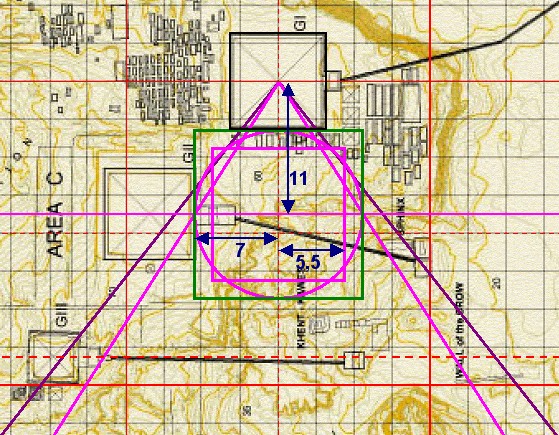
| Ausgangspunkt ist die
Chefren-Quadratur. Der Abstand der Chefren-Pyramide von
der Cheops-Pyramide ist gleich der Höhe des
Quadraturdreiecks. y1 = 353,86264 m = 11 Einheiten ==> 1 Einheit = 32,16933091 m |

| Abbildung 8a.1 – Die Chefren-Quadratur im Gizeh-Komplexes von Mark Lehner |
| Trägt man vom Mittelpunkt der
Cheopspyramide 14 Einheiten in
südlicher Richtung ab, dann ergibt sich eine
Waagerechte, die mit den Schenkeln des 14:11
Winkel ein Quadraturdreieck 1 bildet. 14 Einheiten = 450,3706327 m |
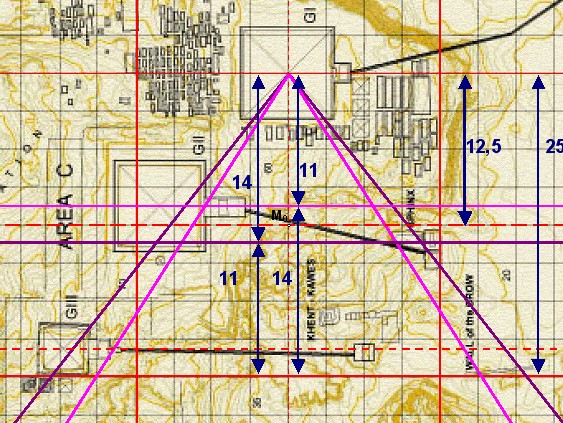
| Abbildung 8a.2 – Abstände im Gizeh-Komplexes von Mark Lehner |
| Aus dem Quadraturdreieck 1 ergibt sich die 14:11 Quadratur |
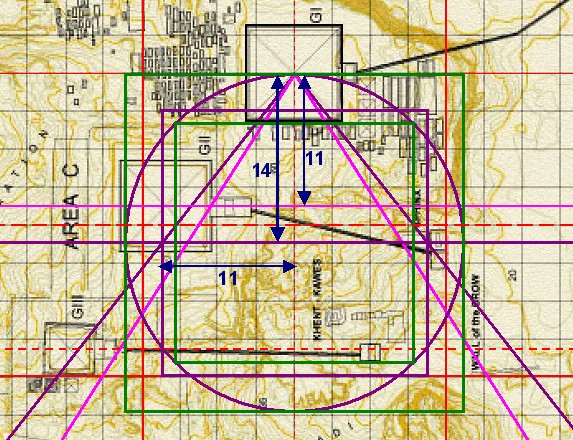
| Abbildung 8a.3 – Die 14:11 Quadratur im Gizeh-Komplexes von Mark Lehner |
| Verlängert man die Basisseite des
Quadraturquadrates der 14:11 Quadratur
erhält man die Basislinie. Diese Linie
stellt ebenfalls die Grundlinie für den
Mykerinos-Komplex dar. Die Basislinie ist 25 Einheiten von der Waagerechten durch den Mittelpunkt der Cheops-Pyramide entfernt. So lässt sich jetzt ein Quadrat mit einer Kantenlänge von 25 Einheiten auf der Basislinie erzeugen. Dieses Quadrat wird im Folgenden Basisquadrat genannt. 25 Einheiten = 804,2332728 m |
| Die Chefren-Quadratur und die 14:11 Quadratur zusammenergeben folgendes Bild: |
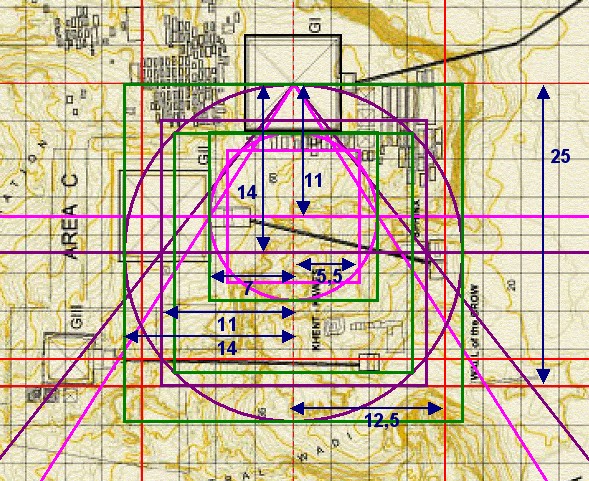
| Abbildung 8a.4 – Die Chefren-Quadratur und die 14:11 Quadratur im Gizeh-Komplexes von Mark Lehner |
| Das Basisquadrat ergibt sich aus der 14:11 Quadratur. In den verschiedenen Karten sieht das folgendermaßen aus: |
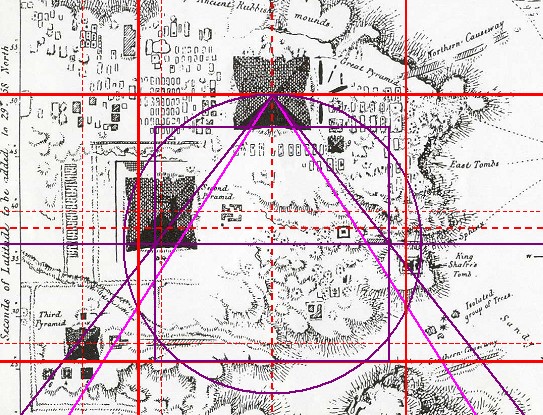
| Abbildung 8a.5 – Basisquadrat im Gizeh-Komplexes von Howard Vyse |
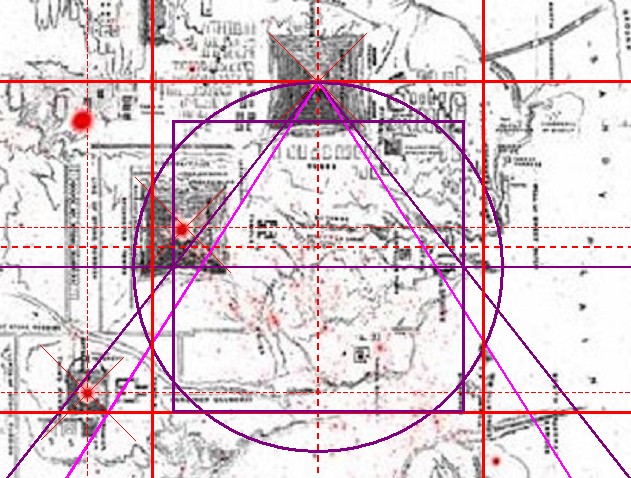
| Abbildung 8a.6 – Basisquadrat im Gizeh-Komplexes von John Perring |
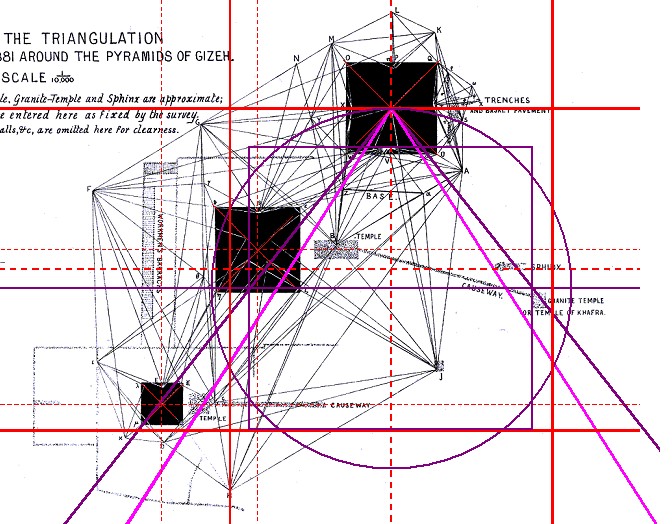
| Abbildung 8a.7 – Basisquadrat im Gizeh-Komplexes von Flinders Petrie |
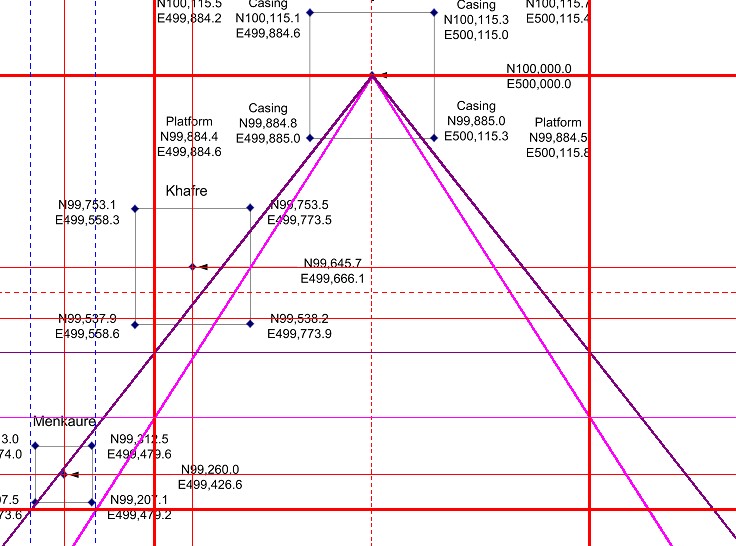
| Abbildung 8a.8 – Basisquadrat im Gizeh-Komplexes von Glen Dash |
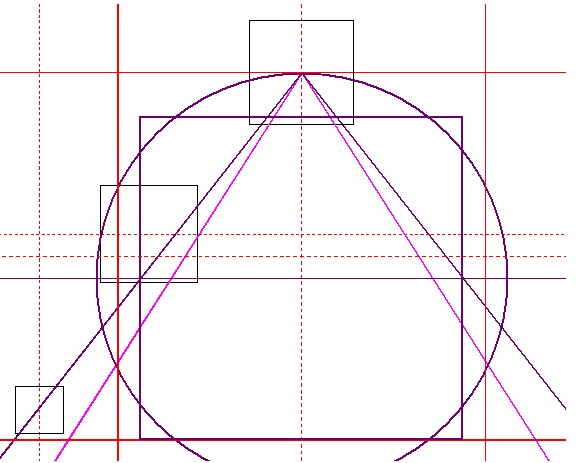
| Abbildung 8a.9 – Die 14:11-Quadratur und das Basisquadrat in der Basiskarte |
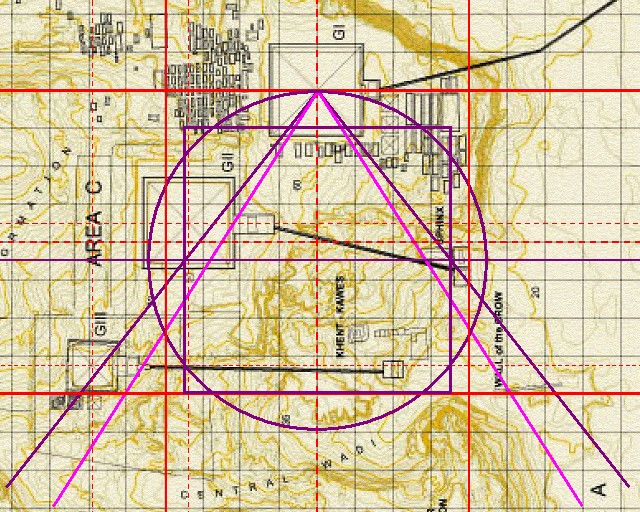
| Abbildung 8a.10 – Basisquadrat im Gizeh-Komplexes von Mark Lehner |
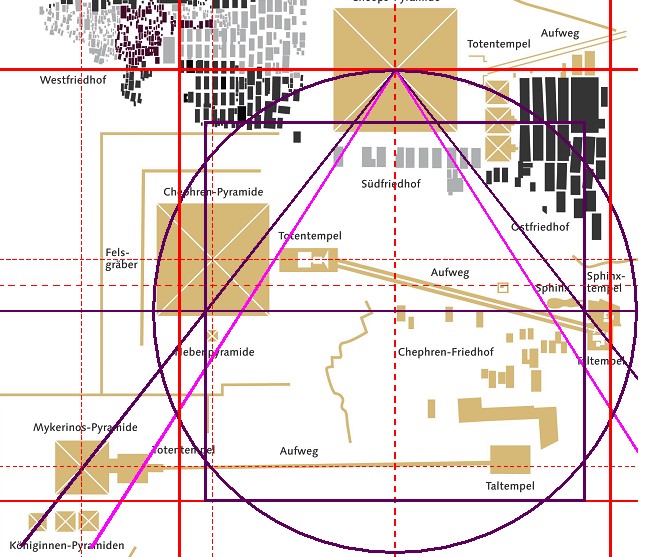
| Abbildung 8a.11 – Eine weitere Karte des Gizeh-Komplexes mit Basisquadrat |
| Für alle
Karten gilt: Die exakte Lage der Sphinx zwischen den östlichen Schenkeln des 14:11 und 11:7 Winkeln, sowie die Lage des Mykerinos-Komplexes auf dem westlichen 14:11 Schenkel und die Lage des Chefren-Komplexes btgl. des westlichen 11:7 Schenkel legen nahe, dass hier tatsächlich die 14:11 und 11:7 Proportion benutzt worden ist. |
| Die Schenkel der 14:11 und
11:7 Winkel bilden Schnittpunkte mit dem Basisquadrat. Es ergeben sich die Schnittpunkte A1, B1, A2, B2 zwischen den Quadraturwinkeln und dem Basisquadrat. Außerdem ergeben sich in der Verlängerung der Basisseite des Basisquadrates noch die Schnittpunkte C1, D1, C2, D2 Da die Punkte A1, A2, und B1, B2 paarweise vorkommen können diese durch waagerechte Linien miteinander verbunden werden. Außerdem ergeben sich noch die Schnittpunkte E1 und E2 sowie die Schnittpunkte F1 und F2. Es kommen noch die Schnittpunkte I1, J1, I2, J2 mit der Halbachse des Basisquadrates hinzu. |
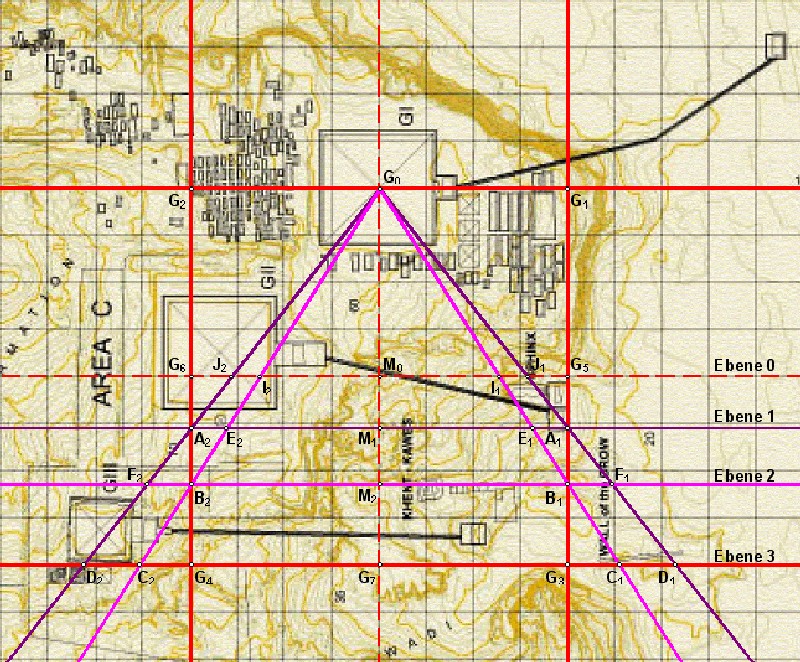
| Abbildung 8a.12 - Alle Schnittpunkte der 14:11 und 11:7 Schenkel mit dem Basisquadrat |
Die Konstruktion in Abbildung 8.12
wird im Folgenden als Basiskonstruktion
des Gizeh-Plateaus bezeichnet. Daraus ergeben sich
insgesamt 8 Quadraturdreiecke und
entsprechende Kreisquadraturen.
8a.4.1 - 14:11 QuadraturDas Quadraturdreieck G0J1J2 mit der Quadratur 0.1.Das Quadraturdreieck G0A1A2 mit der Quadratur 1.1 im Folgenden einfach Quadratur 1 genannt. Das Quadraturdreieck G0F1F2 mit der Quadratur 2.1. Das Quadraturdreieck G0D1D2 mit der Quadratur 3.1. 8a.4.2 - 11:7 QuadraturDas Quadraturdreieck G0I1I2 mit der Quadratur 0.2.Das Quadraturdreieck G0E1E2 mit der Quadratur 1.2 Das Quadraturdreieck G0B1B2 mit der Quadratur 2.2 im Folgenden einfach Quadratur 2 genannt.. Das Quadraturdreieck G0C1C2 mit der Quadratur 3.2. Auf den folgenden Seiten werden die einzelnen Quadraturen ausführlich behandelt. |