
GIZEH - GEODÄTISCHE ERKENNTNISSE
Copyright © Klaus Piontzik
| Es existiert eine
Näherungskonstruktion für die Quadratur des Kreises,
die auf einem Dreieck mit dem Höhen-Basis-Verhältnis
14:22 beruht. Der Radius des Kreises ist die Höhe des Dreiecks und die Quadratseite ist gleich der Basisseite des Dreiecks. Kreis und Quadrat besitzen dann den gleichen Umfang. Die Konstruktion wird Quadratur 1 genannt. |

| Abbildung 7.1 - Quadratur 1 |
| Nimmt man ein rechtwinkliges Dreieck, (in Abbildung 7.2 entsprechend den Schnitt- Dreiecken MBC bzw. MAC) mit dem Seiten/Höhen - Verhältnis 11:14, so läßt sich daraus auch die komplette Quadratur 1 aus Abbildung 7.1 ableiten. |
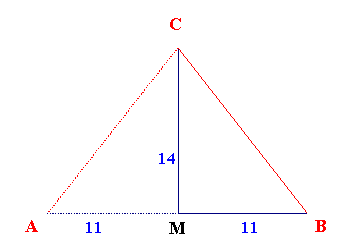
| Abbildung 7.2 - Quadraturdreieck 1 |
| Es existiert eine
Näherungskonstruktion für die Quadratur des Kreises,
die auf einem Dreieck mit dem Höhen-Basis-Verhältnis
11:14 beruht. Der Durchmesser des Kreises ist gleich der Basisseite des Dreiecks und die Höhe des Dreiecks ist gleich der Quadratseite. Kreis und Quadrat besitzen dann den gleichen Umfang. Die Konstruktion wird Quadratur 2 genannt. |

| Abbildung 7.3 - Quadratur 2 |
| Man kann bei der Quadratur 2 das Quadrat noch zentrieren. |

| Abbildung 7.4 - Quadratur 2 zentriert |
| Nimmt man ein rechtwinkliges Dreieck, (in Abbildung 7.5 entsprechend den Schnitt- Dreiecken MBC bzw. MAC) mit dem Höhen/Seiten - Verhältnis 11:7, so läßt sich daraus auch die komplette Quadratur aus Abbildung 7.3 bzw. 7.4 ableiten. |

| Abbildung 7.5- Quadraturdreieck 2 |
| Quadratur 1 und 2 lassen sich zusammen legen, indem die Spitzen beider Dreiecke zusammen fallen. Beide Dreiecke erzeugen dieselbe Quadratur. |

| Abbildung 7.6 - Quadratur 1 und 2 |
| Zum Abschluß der Quadratur kann man den Kreis noch mit dem zugehörigen Inquadrat und Umquadrat versehen. |

| Abbildung 7.7 - Gesamtquadratur mit Inqudrat un Umquadrat |
| Die Abbildung 7.7 wird im Folgenden als Gesamtquadratur bezeichnet. |