GIZEH - GEODÄTISCHE ERKENNTNISSE
Copyright © Klaus Piontzik
| Die Schenkel des 11:14
Winkels schneiden die Waagerechte
B1M2B2,
also die Hauptachse von Quadratur 2 in
den Punkten F1
und F2. Die Quadratur 2.1 wird durch das Quadraturdreieck G0F1F2 gebildet, mit dem 11:14 Verhältnis. |

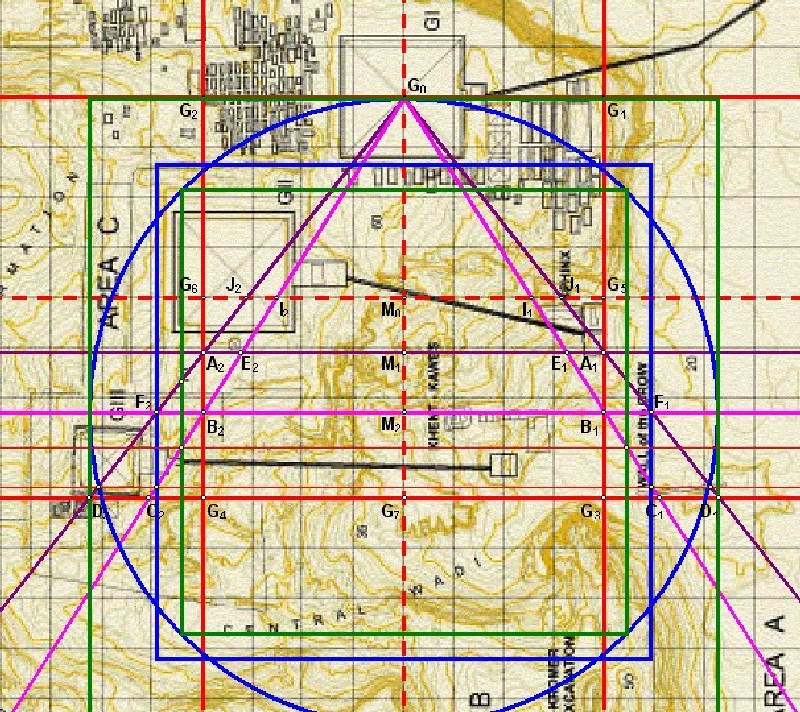
| Abbildung 10.1 - Die Quadratur 2.1 in der Karte von Mark Lehner |
Bezüge zu architektonischen Teilen:Das Inquadrat der Qudratur 2.1 bildet die Westseite der Chefren-Pyramide und gleichzeitig das östliche Ende des Mykerinos-Tempels.Die Schnittpunkte der 11:14 Schenkel mit dem Quadraturkreis 2.1 und die Schnittpunkte der 7:11 Schenkel mit dem Quadraturquadrat 2.1 liegen auf einer waagerechten Linie. Diese Linie bildet die Nordseite der Mykerinos-Pyramide. |
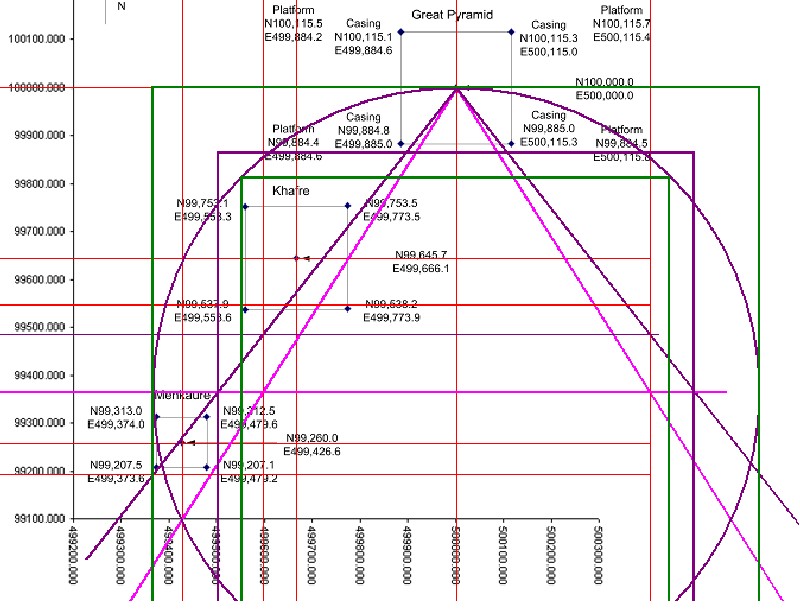
| Abbildung 10.2 - Die Quadratur 2.1 in der Karte von Glen Dash |
| Es ergeben sich wieder Schnittpunkte zwischen den 7:11 und 11:14 Schenkeln mit der Quadraturkonstruktion 2.1 und entsprechende Waagerechte. |
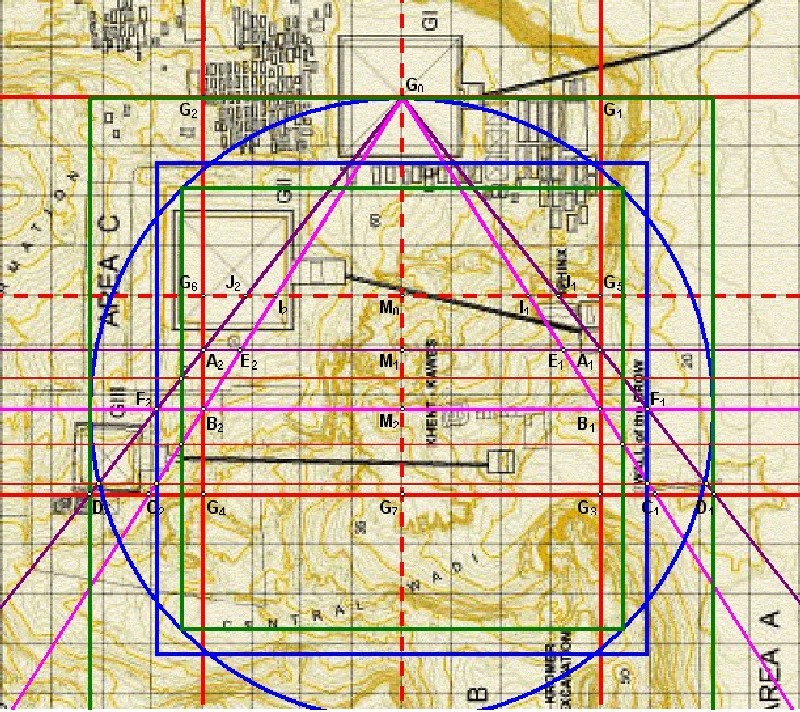
| Abbildung 10.3 - Die Quadratur 2.1 mit Schnittpunkten in der Karte von Mark Lehner |
| Die Schnittpunkte der 7:11
Schenkel mit dem Quadraturquadrat 2.1
liegen auf der gleichen Linie wie die Schnittpunkte der 11:14
Schenkel mit dem Quadraturkreis 2.1. Die erzeugte Waagerechte bildet die Basislinie der Mykerinos-Pyramide |