GIZEH - GEODÄTISCHE ERKENNTNISSE
Copyright © Klaus Piontzik
| Die Schenkel des 14:11
Winkels schneiden das Basisquadrat in
den Punkten A1
und A2,
sowie in den Punkten D1
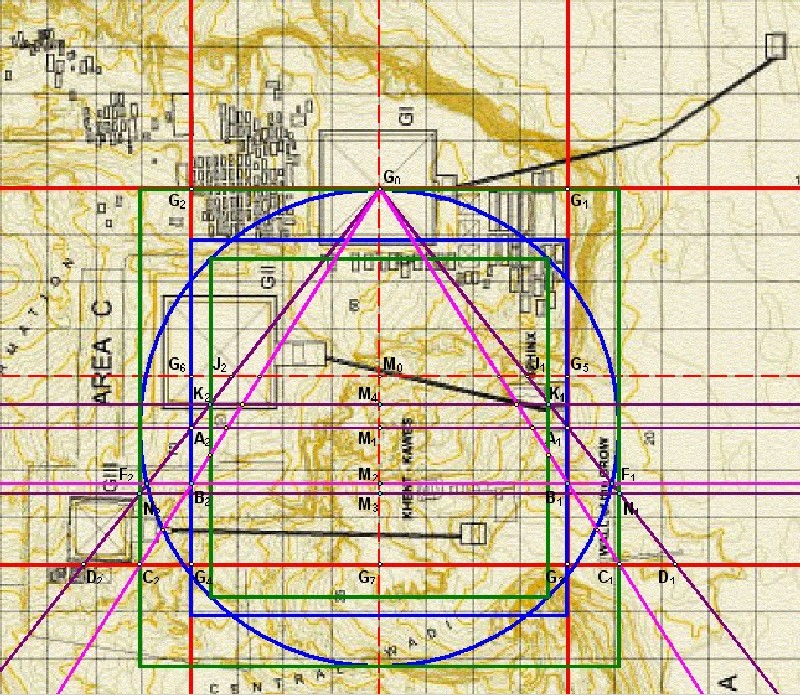
und D2. Dadurch werden die Quadraturdreiecke G0A1A2 und G0D1D2 gebildet. Laut Definition in Kapitel 8a liefert das Dreieck G0A1A2 die Quadratur 1.1 und das Dreieck G0D1D2 die Quadratur 3.1 (sieke Kapitel 11) Im folgenden wird Quadratur 1.1 hier weiter einfach als Quadratur 1 bezeichnet. |

| Abbildung 9.1 - Die Quadratur 1.1 in der Mark Lehner Karte |
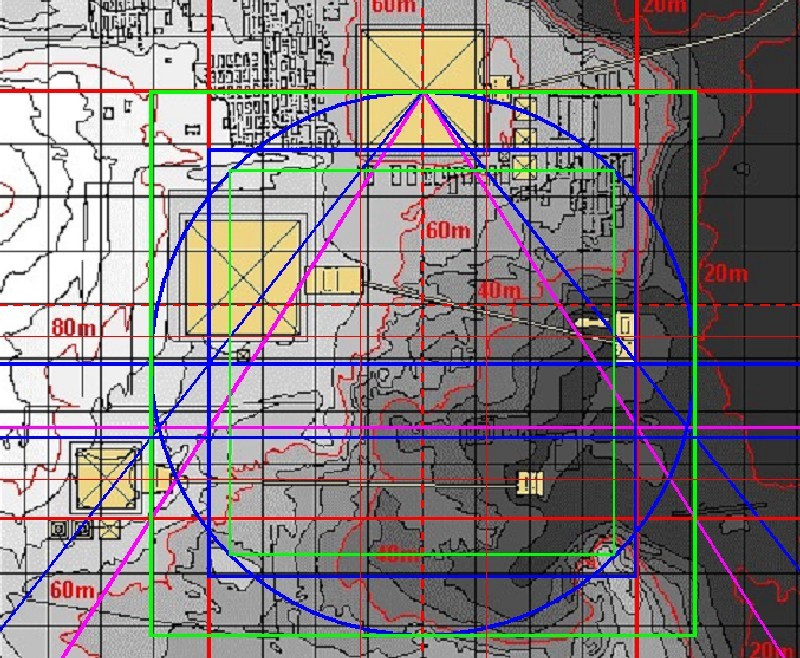
| Abbildung 9.2 - Die Quadratur 1.1 in der Satellitenkarte |
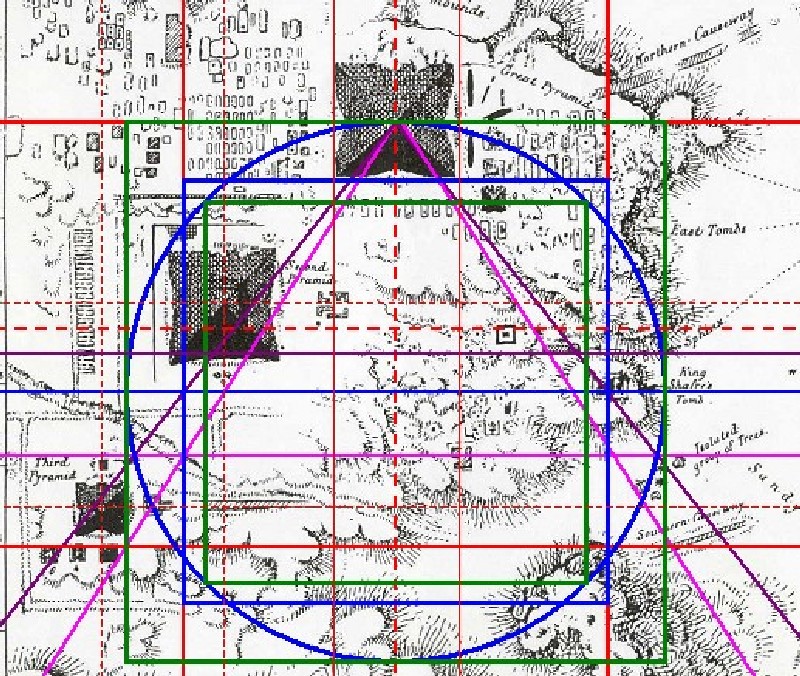
| Abbildung 9.3 - Die Quadradur 1.1 in der Howard Vyse Karte |
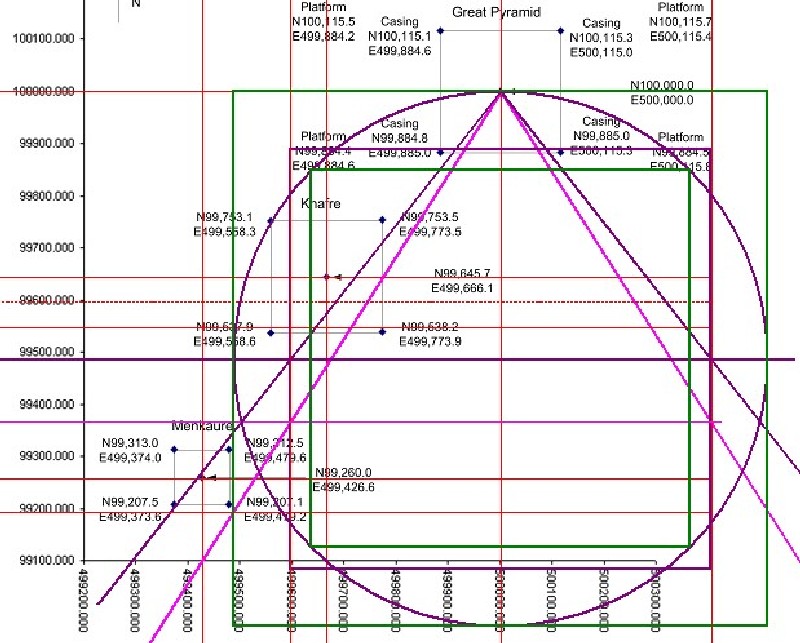
| Abbildung 9.4 - Die Quadradur 1.1 in der Glen Dash Karte |
| Bemerkung: Das Quadraturquadrat 1.1 ist gleich dem Basisquadrat. |
| Auffallend ist, dass der Taltempel des Chefren genau in der Ecke des Quadraturdreiecks 1.1 beim Punkt A1 liegt. |
| Es ergeben sich weitere Schnitpunkte der 7:11 und 11.14 Schenkel mit der Quadraturkonstruktion 1.1. Und damit auch weitere waagerechte Verbindungen. Einzeichnen aller Schnittpunkte und der dazu gehörigen Waagerechten ergibt die folgende Abbildung: |
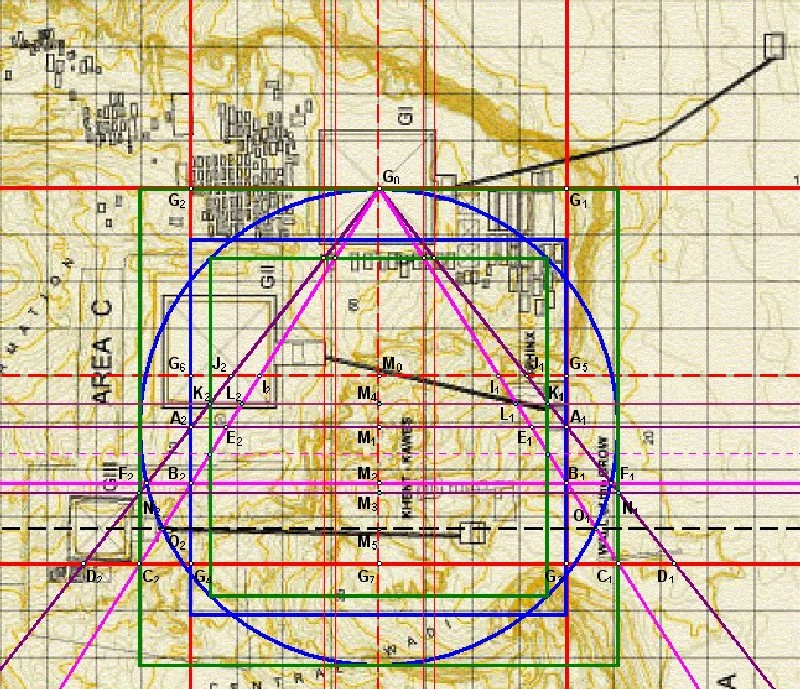
| Abbildung 9.4 - Die Quadradur 1.1 und alle Schnittpunkte in der Mark Lehner Karte |
| Bezüge
zu architektonischen Teilen: Die Sphinx liegt genau zwischen dem 7:11 und 11:14 Winkel der östlichen Schenkel. Der Taltempel des Chefren liet genau in der Ecke des Quadraturdreiecks 1.1 beim Punkt A1. Der Schnittpunkt des 11:14 Winkels mit dem Inquadrat liefert die Waagerechte K2, L2, M4, L1, K1 und ergibt die Nordseite der Chefren-Pyramide. Sowie die Basislinie für die Sphinx und als Trennlinie zwischen Chefren- und Sphinx-Taltempel. Das Inquadrat ergibt die Westseiten der Taltempel der Sphinx und von Chefren |
| Der Schnittpunkt des 11:14
Winkels mit dem Umquadrat liefert die
Waagerechte N2M3N1
und damit das Quadraturdreieck G0N1N2
Dies wird im folgenden Quadraturdreick 4 genannt. Die darauf basierende Quadratur 4 ist in der folgenden Abbildung in violett abgebildet, sowie das zugehörige Um- und Inquadrat in grün. |
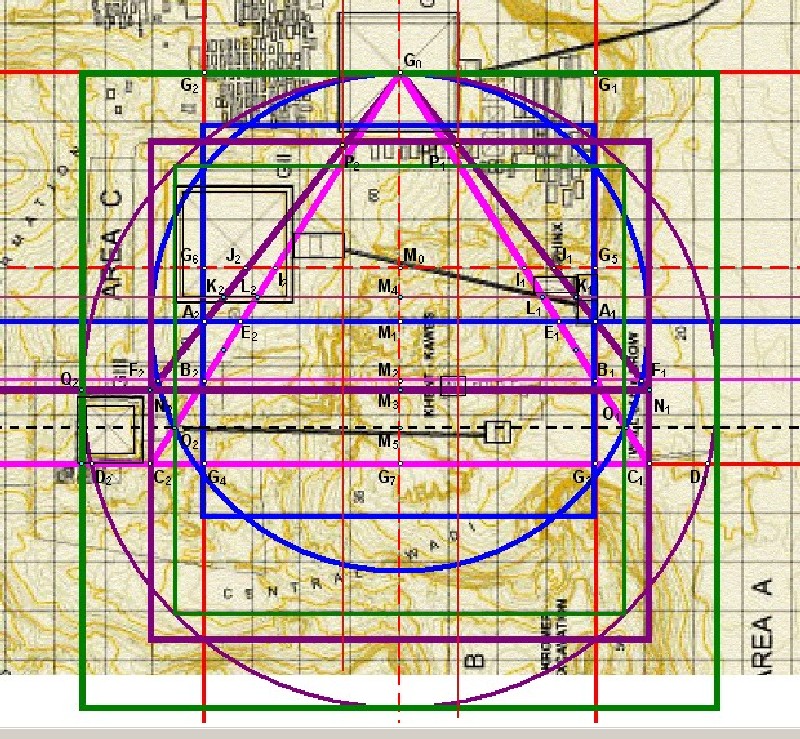
| Abbildung 9.5 - Die Quadradur 4 in der Mark Lehner Karte |
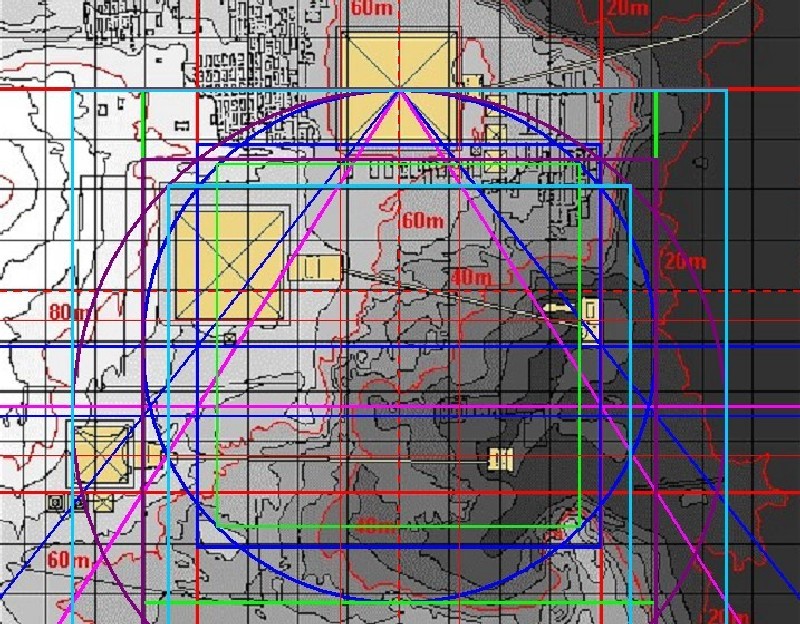
| Abbildung 9.6 - Die Quadradur 4 in der Satelliten-Karte |
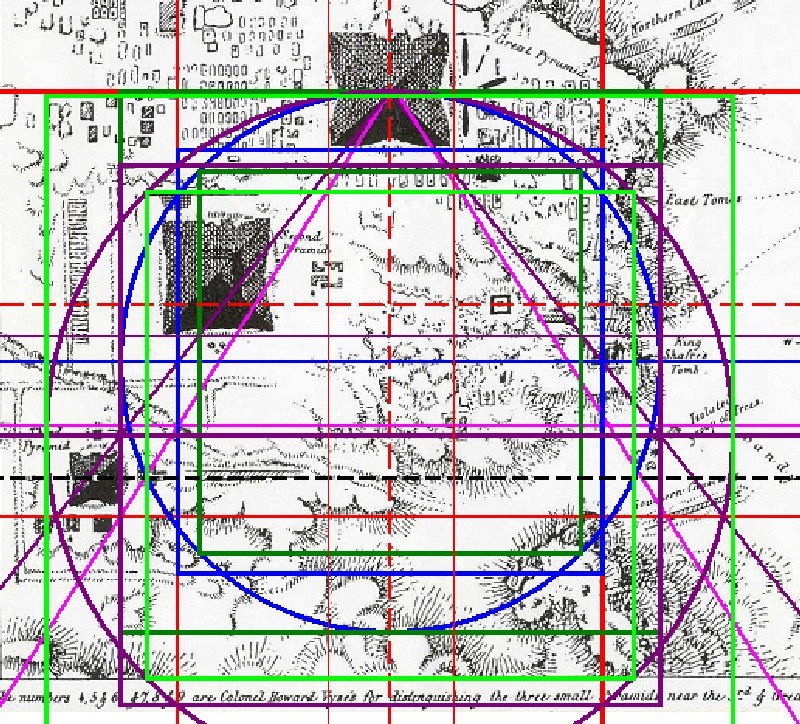
| Abbildung 9.7 - Die Quadradur 4 in der Howard Vyse-Karte |
| Bezüge
zu architektonischen Teilen: Durch die Quadtratur 1.1 sowie den Waagerechten die durch die Schnittpunkte erzeugt werden, ergeben sich 3 Seiten des Mykerinos-Komplexes. 1) Die Basisseite des Basisquadrates mit D2, C2, G4, G7, G3, C1, D1 ergeben die Südseite des Mykerinos-Kompelxes 2) Der Schnittpunkt des 11:14 Winkels mit dem Umquadrat liefert die Waagerechte N2M3N1 und ergibt die Nordseite des Mykerionos-Komplexes 3) Das Umquadrat des Quadraturkreises 1.1 bildet mit N2, C2 die Ostseite des Mykerinos-Komplexes 4) Die Waagerechte O2M5O1 geht durch den Mittelpunkt der Mykerions-Pyramide Auch das Grab des Chentkaues ist durch entsprechenden Waagerechten und Senkrechten genau verortet. |
| Bemerkung Das Quadraturquadrat 4 ist gleich dem Umquadrat des Quadraturkreises 1.1 |
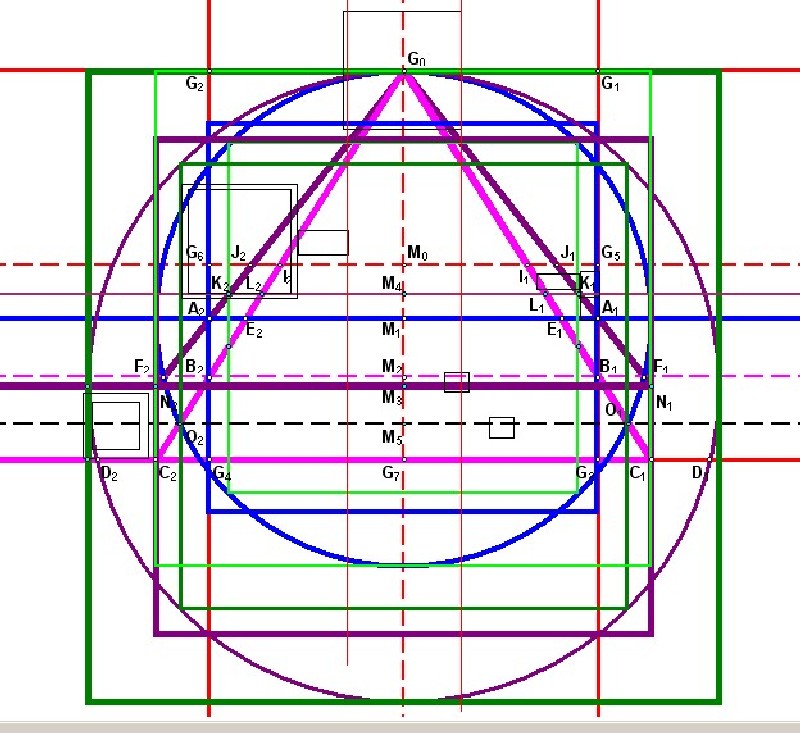
| Abbildung 9.8 - Der Bauplan für die Mykerinos-Pyramide |