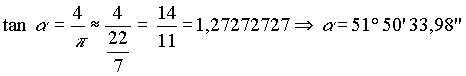7a.9.1
– Längen
Die kleinste ägyptische Längeneinheit war das Djeba.
Djeba war die Bezeichnung der Maßeinheit
„Finger“ (englisch digit), der 1,87 Zentimeter
maß.
4 „Finger“ ergaben die Länge einer Handbreite
(Schesep)
20 „Finger“ ergaben einen Oberarm (Remen)
24 „Finger“ ergaben eine kleine Elle
(meh-scherer)
28 „Finger“ ergaben eine Königselle (Meh)
Schesep, auch shep oder
henet, (englisch palm) war die altägyptische Bezeichnung
der „Handbreite“, die 7,5 Zentimeter maß.
7 Schesep ergaben eine Königselle (Meh)
6 Schesep ergaben die kleine Elle (meh-scherer), mit ca.
0,45 Meter.
5 Schesep ergaben ein Remen, mit ca. 0,374 Meter
Meh, auch meh-nesut, (englisch cubit),
war die altägyptische Bezeichnung der
„Königselle“, die ca. 0,524 Meter maß.
1 Meh = 7 Schesep = 28 Djeba
1 meh-scherer = 6 Schesep = 24 Djeba
7a.9.2
– Messschnüre
Die sogenannten Harpedonapten (griechisch:
„Seilspanner“; Zusammensetzung aus harpedonä =
Seil und hapto = anfassen, anknüpfen) waren die
Feldvermesser im alten Ägypten. Sie allein waren
zuständig für die Bestimmung von Winkeln und vermaßen
Bauwerke und Grundstücke im Auftrag des Pharao.
Für die Bestimmung von Winkeln verwendeten die
Harpedonapten Schnüre verschiedener Länge. Die drei
grundlegenden Schnüre hatten die Längen:
84 Schesep - lange Schnur = 12 Meh
(Königselle)
72 Schesep - mittlere Schnur = 12
meh-scherer (kleine Elle)
60 Schesep - kurze Schnur
Die drei grundlegenden Schnüre wurden bei Bedarf noch
proportional verkleinert, indem man sie in 12
Abschnitte unterteilte.
Die lange Schnur ist in Abschnitte zu 7 Schesep
aufgeteilt.
Die mittlere Schnur ist in Abschnitte zu 6 Schesep
aufgeteilt.
Die kurze Schnur ist in Abschnitte zu 5 Schesep
aufgeteilt.
Die Schnüre basieren auch auf dem pythagoreischen Tripel
3 : 4 : 5. Durch Verlängerung der
kurzen Schnur auf eine Länge von 70 Schesep (10 Meh)
oder Verkürzung der mittleren Schnur erhielten sie die
Möglichkeit der Aufspannung des pythagoreischen Tripels 20
: 21 : 29.
Das kurze Stück der Schnur wird als Kathete mit 20
Schesep dabei senkrecht aufgespannt. Diese Aufspannung
ist der direkte Verbindung zwischen den beiden
pythagoreischen Zahlen-Tripel.
Weitere Beispiele für pythagoreische
Zahlen-Tripel:
Tripel (5, 12, 13), (8, 15, 17), (7, 24, 25), (12, 35,
37), (9, 40, 41)
Summe 30 40 56 84 90
7a.9.3
– Winkel
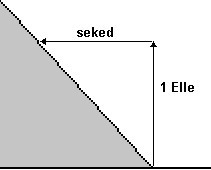 |
Das Seked
(seqt) würde man heute als Maß für
Steigungswinkel bezeichnen. Die Ägypter kannten
aber keine Einteilung der Winkel in 360°.
Es wurde nicht der Winkel der Neigung gemessen,
sondern um wie viele Handbreit (Schesep) und
Finger (Djeba) die obere Kante der Mauer zur
unteren Kante zurückversetzt war, und zwar bei
einer Standardhöhe von einer königlichen Elle. |
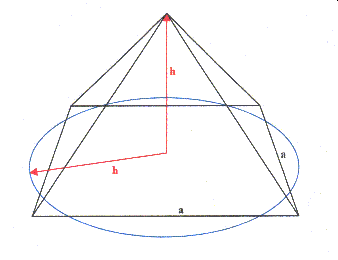
Allgemein gesehen
wird hier eine senkrechte Komponente mit einer
waagerechten Komponente verglichen. Wobei die senkrechte
Komponente normiert wird, indem sie auf einen Standard
von 1 Königselle (1 Meh = 7 Schesep) gesetzt wird.
Zum Abschluss wird die waagerechte Komponente als
Steigung (Seked) in Schesep (Handbreite) bestimmt.
Die Definition des Seked würde unserem heutigen Tangens
für den Böschungswinkel entsprechen. Da hier eine
Strecke mit einer anderen verglichen wird, können wir
das, wie die Ägypter, einfach als Proportion betrachten.
Seked = vertikal : horizontal = 1 Königselle : x
dabei ist x eine Länge die in Schesep bestimmt wird
Es gilt: 1 Königselle = 7 Schesep = 28 Djeba
x = 7 Schesep ==> 7 Seked ==> arc tan 7/7 = arc tan
1:1 = 45°
x = 5 Schesep ==> 5 Seked ==> arc tan 7/5 = 54°
27' 44,36''
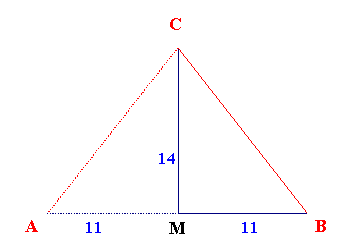
Das 11:14 Verhältnis lässt sich so
darstellen.
11:14 = 7 : x
x = 98/11 Schesep = 8 10/11 Schesep ==> 8
10/11 Seked
Es gilt: arc tan 11/14 = 38° 09' 26,01''
Das 14:11 Verhältnis lässt sich auch
als 7:5½ darstellen. Daraus folgt
x = 5½ Schesep ==> 5½ Seked
Es gilt: arc tan 7/5½ = arc tan 14/11 = 51° 50' 34''
Das 7:11 Verhältnis lässt sich direkt
umsetzen.
x = 11 Schesep ==> 11 Seked
Es gilt: arc tan 7/11 = 32° 28' 16,29''
Das 11:7 Verhältnis lässt sich so
darstellen.
11:7 = 7 :x
x = 49/11 Schesep = 4 5/11 Schesep ==> 4 5/11
Seked
Es gilt: arc tan 11/7 = 57° 31' 43,7''
Für die Chefren-Pyramide wird ein Seked von 5 Schesep
(Handbreit) und 1 Djeba (Finger) angegeben
5 Schesep + 1 Djeba = 21 Djeba
28 Djeba ergaben eine Königselle (Meh)
Für den Winkel gilt: arc tan 28/21 = arc tan 4/3 =
53,13°
Damit beträgt das Steigungsverhältnis der
Chefren-Pyramide 4:3
Für die Mykerinos-Pyramide wird ein Seked von 8 Schesep
(Handbreit) und 3 Djeba (Finger) angegeben
8 Schesep + 3 Djeba = 35 Djeba
28 Djeba ergaben eine Königselle (Meh)
Für den Winkel gilt: arc tan 35/28 = arc tan 5/4 =
51,34°
Damit beträgt das Steigungsverhältnis der
Mykerinos-Pyramide 5:4
Wie gesehen sind die modernen Proportionen und die
altägyptische Darstellungsweise ineinander überführbar
und damit äquivalent.
7a.9.4
– Das Merchet
Mit den Messschnüren bestimmten die Harpedonapten alle
Strecken und auch alle Winkel der ägyptischen Welt.
Dabei nahmen sie das Merchet zur Hilfe
Das Merchet ist ein Messgerät zur Messung von
ägyptischen Böschungswinkeln. Seine Existenz ist durch
eine entsprechende Hieroglyphe bekannt geworden.
Beim Merchet wird die kurze Kathete der Messschnur durch
eine horizontale Holzleiste und die lange Kathete durch
ein senkrecht herunterhängendes Lot ersetzt. Das
Schnurteil der Hypotenuse entfällt.
Ein Merchet auf Grundlage der kurzen Schnur hat eine
Holzleiste von 42 Schesep. Die Hälfte der Leiste ist mit
der Maßeinteilung in Schesep versehen.
An dem Ende der Leiste mit Einteilung ist das Lot mit
einer genauen Länge von 20 Schesep befestigt. Die
Hälfte der Leiste ohne Einteilung dient zur Auflage auf
der oberen Ebene der Böschung. Zur sauberen Messung ist
die horizontale Lage der Leiste einzuhalten.
Der Anfang der Einteilungen musste mit der oberen
Böschungskante übereinstimmen.
Durch Verschiebung der Leiste wird nun der ägyptische
Böschungswinkel mit Ablesung an der oberen
Böschungskante ermittelt.
Die Verwendung der langen Schnur (12 Königsellen oder
Meh) ermöglicht (bei Aufspannung der kurzen Kathete als
Basis) eine unmittelbare Umrechnung von Schesep in Seked.
Dabei wird bis auf Fingerbreite (Djeba) unterteilt.
Das Merchet ist eine Weiterentwicklung der Erkenntnisse
aus der Praxis mit den Schnüren der Harpedonapten.
7a.10 - Konsequenzen
Insgesamt stand den
Ägyptern somit ein differenziertes Instrumentarium zur
Verfügung, um hinreichend genaue Längen- und
Winkelmessungen machen zu können.
Alle Betrachtungen zu Proportionen in
dieser Abhandlung sind direkt übertragbar in
altägyptische Steigungen und das hier benutzte
Proportionsmodul für die Quadraturen ist äquivalent
zur altägyptischen Darstellungsweise, bzw.
lässt sich in diese transformieren.
Daher können alle hier gemachten Betrachtungen, ohne
Einschränkung der Allgemeinheit, weiterhin auf der
Grundlage der modernen Proportionsbildung stattfinden.
Eine Umrechnung in ägyptische Einheiten ist also nicht
unbedingt erforderlich.
|