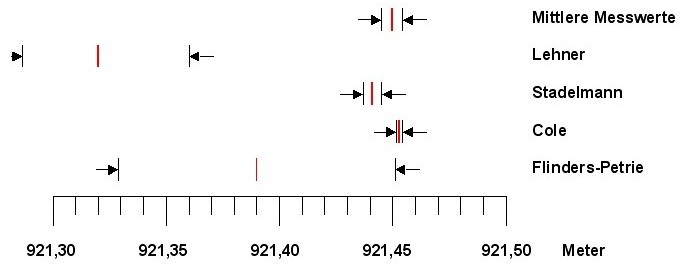
| Die obere Grenze des Petrie-Umfanges liegt
nur 0,8 mm unter dem Minimum-Wert von
Cole. Das Petrie-Fenster grenzt also im oberen Bereich an
das Cole-Fenster. Damit wird das Flinder-Petrie Fenster
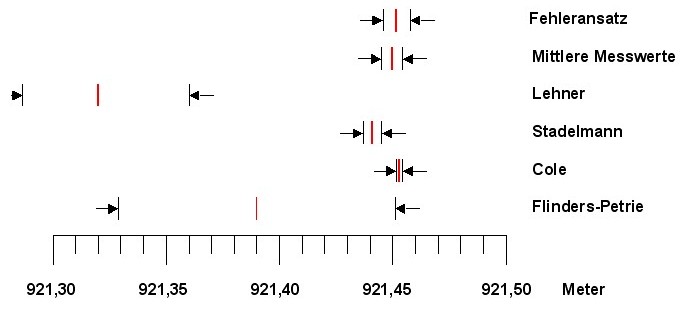
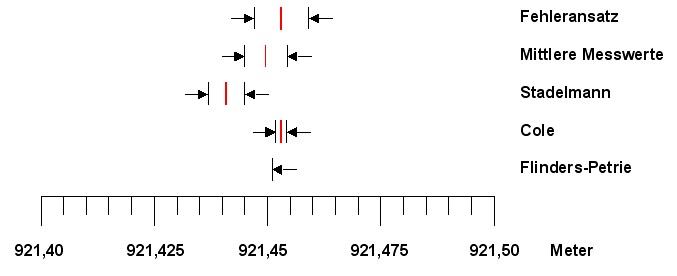
nachträglich durch Cole in etwa bestätigt. Betrachten wir die Fehlertoleranzen. Petries Umfang ist mit einem Fehler von 6 cm behaftet, und wäre damit für weitere Berechnungen auch ungeeignet. Coles Fehlertoleranz liegt bei 1,2 mm. Das Fenster von Stadelmann liegt ganz im oberen Bereich des Petrie-Fensters. Damit wird das Flinder-Petrie Fenster nachträglich durch Stadelmann in etwa bestätig.t. Das Fenster von Stadelmann liegt etwas unterhalb des Cole-Fensters. Die Differenz der Mittelwerte beträgt nur 1,2 cm. Petries Messung wäre demnach 6,3 cm zu kurz geraten. Das Fenster von Cole wird von Stadelmann und von Petrie bestätigt. In den weiteren Betrachtungen und Berechnungen wird daher der Umfangswert von Cole, aufgrund seiner Genauigkeit,verwendet als Orientierungswert verwendet.. Gegenüber
Coles Wert ist Lehners Wert um 13,3 cm
zu kurz geraten. Wie weiter oben schon erwähnt stellt
sein Wert eine Rekonstruktion dar und lässt sich darauf
zurück führen, dass seit der Messung von Cole bereits
einiges der Bausubstanz durch Verwitterung und anderer
Erosionen verloren gegangen ist. Der Wert von Lehner wird
daher in den weiteren Berechnungen nicht mehr
berücksichtigt.
4.1.6 - SockelumfangDen Umfang des Sockels berechnete Fix aus den vorliegenden Meßwerten, d.h. aus den Messungen die Flinders-Petrie und Cole vorgenommen hatten. Er erhielt als Ergebnis : Der Sockelumfang der großen Pyramide (Fix): US1 : 3043,533 ft = 927,6688584 m Fix interpretierte diesen Wert als den 43200ten Teil des Erdäquators. Fälschlicherweise wird dieser Wert oft so behandelt, als stamme er aus der Messung von Flinders-Petrie oder von Cole. Wir sollten uns aber vor Augen führen, dass dies eine rein errechnete Größe ist. Sie ist darum mit der nötigen Vorsicht zu handhaben, d.h. sie ist nicht so ohne weiteres mit den anderen Meßwerten kombinierbar. Was allerdings einige Autoren nicht daran gehindert hat, dies trotzdem zu tun. 4.1.7 - MeßwerteEine andere unkorrekte Art mit Meßwerten umzugehen, besteht darin diese zu runden. Die Messungen von Petrie-Flinders und von Cole sind mit dem englischen Maßsystem getätigt worden. Bei der Umrechnung ins metrische System treten dann natürlich wesentlich mehr Stellen hinterm Komma auf, als bei den ursprünglichen Werten. Dies wird dann als Argument benutzt, um die metrischen Daten auf die signifikante Stellenzahl zu runden. Ein Beispiel dafür finden wir in dem Buch "Die kosmische Oktave" von Cousto. Auf Seite 82 gibt er die gerundeten Seitenlängen von Cole an. Bildet man allerdings die Summe aus den Längen, so erhält man einen Wert, der kleiner ist als der Basisumfang. Die auftretende Differenz beträgt etwa 2 cm. Als wissenschaftlich kann man diese Vorgehensweise wirklich nicht bezeichnen. Um die ursprüngliche Maßgenauigkeit zu erhalten, gibt es nur zwei Möglichkeiten. Entweder man verbleibt im englischen Maßsystem, oder bei der Umrechnung von einem System in ein anderes müssen die anfallenden Kommastellen stehen bleiben. Auch wenn es lästig oder unsinnig erscheint mit 6 bis 8 Stellen hinterm Komma zu operieren. |