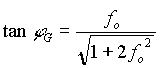GIZEH - GEODÄTISCHE ERKENNTNISSE

1 - Bestimmung der geographischen Breite von Gizeh

1.1 - Zur Gestalt der Erde

Geodätische Systeme stellen Näherungsmodelle der Erdgestalt dar. Ausgehend von einem Rotations - Ellipsoiden versuchen solche Systeme Parameter zu definieren, die eine immer genauere Beschreibung der Erde in ihrer 3-dimensionalen Ausdehnung erlauben.
		Ausgangspunkt ist, in der Regel, eine Ellipse mit der großen Halbachse a und der kleinen Halbachse b. Lässt man nun die Ellipse um die kleinere Achse rotieren, so entsteht ein sogenanntes Rotationsellipsoid, welches auch als Sphäroid bezeichnet wird. Bei genügend hoher Genauigkeit der Beobachtung, stellt sich allerdings heraus, dass ein ellipsoidisches Erdmodell als exakte Lösung nicht ausreichend ist.
Abbildung 1.1 - Entstehung eines Rotationsellipsoids

Die Figur der Erde wird durch eine physische und durch eine mathematische Oberfläche beschrieben. Unter der physischen Erdoberfläche versteht man die Begrenzung zwischen festen und flüssigen Erdmassen gegenüber der Atmosphäre. Hier findet ja sozusagen ein Dichtesprung im Aufbau der Erde statt, und zwar von der mittlere Dichte der oberen Erdkruste mit r = 2,7 gcm^-3 auf die Luftdichte mit r = 0,0013 gcm^-3.

Die unregelmäßig gestaltete Oberfläche der festen Erdmassen wie z.B. die Kontinente lässt sich aber nicht so ohne weiteres durch eine mathematische Beziehung darstellen. Hier hilft nur die Punktweise Erfassung und Kartographierung. Üblicherweise geschah dies in 5° x 5° oder auch in 1° x 1° Unterteilungen.

Die Oberfläche der Ozeane, die immerhin etwa 70% der Erdoberfläche ausmachen, weist jedoch ein Bildungsgesetz auf. Unter bestimmten Vorraussetzungen bilden die Meere eine Fläche, auf der ein konstantes Schwerepotential herrscht. Sie ist dann Niveaufläche des Erdschwerefeldes
Denkt man sich diese Fläche unter die Kontinente fortgesetzt, so erhält man die mathematische Erdfigur. J.B. Listing gab dieser Niveaufläche 1872 den Namen Geoid.

Die Erde ist aufgebaut aus Massen unterschiedlicher Dichte, die allerdings nicht gleichmäßig heißt homogen verteilt sind. Daher kann es lokal vorkommen, dass die physische (gemessene) Lotrichtung nicht mit der Ellipsennormalen übereinstimmt. Diese Lotabweichungen müssen mit berücksichtigt werden.

Diese Abweichungen werden als Geoidundulationen bezeichnet. Daher wird, in der Regel, ein Referenzellipsoid angenommen, und die auftretenden Höhen über der Ellipsoidoberfläche aufgetragen.

Bei den bis heute getätigten Geoidbestimmungen hat sich gezeigt, dass die Abweichungen des Geoids von einem mittleren Rotationsellipsoiden kleiner als 100 Meter in der Höhe betragen.

		Um eine, noch bessere Anpassung an den Geoid zu erhalten, als ein zweiachsiges Rotationsellipsoid, wäre geometrisch gesehen, der nächste Schritt, es mit einem dreiachsigen, also echtem Ellipsoiden zu versuchen. In der Abbildung 18 ist ein solcher Ellipsoid dargestellt. Bezogen auf die Erde ist dann a₁ dabei die große Äquatorhalbachse, a₂ die kleine Äquatorhalbachse und b die Polachse.
Abbildung 1.2 - (echter) dreiachsiger Ellipsoid

Es sind mehrfach Versuche unternommen worden, die Parameter für ein dreiachsiges Ellipsoid als Erdmodell zu bestimmen.
Die Ergebnisse sind jedoch voneinander different, und zwar wegen der unterschiedlichen Verteilung der Beobachtungen auf der Erdoberfläche und den verschiedenen Methoden die bei der Reduktion auf das Ellipsoid angewandt wurden.

Da die Abweichungen des zweiachsigen Rotationsellipsoiden vom Geoid, in der Regel, in derselben Größenordnung liegen wie die Achsendifferenz von 69 Meter, wird eine wesentlich bessere Anpassung an das Geoid durch ein dreiachsiges Ellipsoid eigentlich nicht erreicht.

Andererseits dagegen werden geodätische Berechnungen durch eine kompliziertere Geometrie des Ellisoids ziemlich erschwert. Auch als geophysikalische Normalfigur ist das dreiachsige Ellipsoid schlechter geeignet, da sich mit den Werten für die Erdmasse und der Winkelgeschwindigkeit der Erde eine unnatürliche Form ergibt. Das dreiachsige Ellipsoid hat sich daher als Bezugskörper in der heutigen Geodäsie nicht durchgesetzt.

Genau genommen rangieren das mittlere Rotationsellipsoid bzw. das Geoid und das dreiachsige Ellipsoid, bzgl. der Abweichungen der tatsächlichen Erdgestalt, in derselben Größenordnung. Sie sind dem zufolge auch gleichwertige Modelle.

1.2 - Die Schmiegekreiskonstruktion

Die Schmiegekreise spielen bei der Ellipse eine besondere Rolle. Einerseits kann mit ihnen die Ellipse relativ schnell konstruiert werden. Andererseits werden die Radien der Schmiegekreise, speziell der kleinere Radius, benutzt, um die Ellipse in ihren Eigenschaften zu beschreiben, z.B. die Ellipse als Kegelschnitt.
Die Frage die sich hier erhebt ist, ob es Bezüge der Ellipsenkonstruktion zum Gizeh-Komplex gibt.

Hier erst einmal die Konstruktion für die Schmiegekreise:

Abbildung 1.3 - Konstruktion der Schmiegekreise

Man konstruiert zuerst das Rechteck MACB - aus der großen Halbachse a und der kleinen Halbachse b.
Eine Diagonale dieses Rechtecks wird eingezeichnet, und zwar die von Punkt A nach Punkt B (blau) .
Auf dieser Diagonalen wird die Senkrechte (blau) errichtet, und zwar so dass diese durch den Punkt C geht. Diese Linie wird hier als Schmiegekreisgerade bezeichnet.
Dann sind die Schnittpunkte (M₁ und M₂) der Schmiegekreisgeraden mit den Ellipsenachsen, die gesuchten Mittelpunkte der Schmiegekreise.

1.3 - Ableitung der geographischen Breite

Bei dieser Konstruktion fällt auf der Schmiegekreisgeraden noch ein weiterer Schnittpunkt an. Nämlich der Schnittpunkt der Gerade mit der Diagonalen. Dieser Punkt wird hier mit S_G bezeichnet. Schmiegekreisgerade und Diagonale stehen ausserdem senkrecht aufeinander. Das ist in der folgenden Abbildung 1.4 noch einmal vergrössert zu sehen

Abbildung 1.4 - Der Schnittpunkt und die Schnittebene

Die Koordinaten des Schnittpunktes S_Glassen sich rein analytisch, also mathematisch, ermitteln. Ebenso der Breitengrad auf dem der Punkt G liegt. Die komplette Ableitung für den Schnittpunkt lässt sich hier nachvollziehen:

Die Gestalt der Erde-10 - Die Schmiegekreise

Der zu G gehörende Breitenkreis ist ein ausgezeichneter Breitenkreis, da er sich direkt auf die Schmiegekreis- Konstruktion bezieht. Der Breitenkreis definiert die Schnittebene in der der Punkt S_Gliegt mit Phi = +29° 58' 19-20,5" N

1.4 - Der Vergleich mit dem Gizeh-Komplex

Insgesamt ergibt sich für die geographische Breite von G:

Einsetzen von n (bzw. von f_o ) in die Gleichungen liefert die folgende Tabelle :

n	Phi

296	29° 58' 19,06"
297	29° 58' 19,40"
298	29° 58' 19,73"
299	29° 58' 20,07"
300	29° 58' 20,40"

Tabelle 1.1

Die geographische Lage der großen Pyramide von Gizeh wird z.B. von Jean Philippe Lauer in seinem 1974 erschienen Buch "Das Geheimnis der Pyramiden" auf Seite 209 mit 29° 58' 51" N angegeben. Nimmt man die Karte von Howard Vyse und ermittelt dort den Standort der Cheops-Pyramide, so erhält man: 29° 58' 51" ± 0,2" N


		Trägt man nun die Werte aus der Tabelle in die Karte von Howard Vyse ein, so ergibt sich das folgende Bild:
Abbildung 1.5 - Die Basislinie in der Vyse-Karte


		Eine noch bessere Übersicht erhält man, wenn diese Werte in eine modernere Karte eingetragen werden:
Abbildung 1.6 - Die Basislinie des Gizeh-Komplexes

Es ist deutlich zu sehen, dass der Streifen, der durch die Werte aus allen geodätischen Systemen gebildet wird, die Basis des Gizeh-Komplexes darstellt. Der Winkeldifferenz Delta Phi = 1,34" entsprechen etwa 41 Meter in Länge.

Der Schnittpunkt S_G der Schmiegekreisgeraden mit der Ellipsen-Diagonale wird auf den Ellipsenumfang übertragen und man erhält die Basislinie für Gizeh.

1.5 - Weitere Mittelwerte

Das geometrische Mittel für die Radien bzw. Durchmesser einer Ellipse: g = Wurzel ( a× b) = a× Wurzel ( f)

Das arithmetrische Mittel für die Radien bzw. Durchmesser einer Ellipse: m = = ½× a× (1+f )

Das harmonische Mittel für die Radien bzw. Durchmesser einer Ellipse: h = 2× a× b = 2× a× f

Für die untere Grenze gilt: y = ½× b

Für die obere Grenze gilt: y = ½× a

Ausführliche Ableitungen lassen sich hier einsehen:

Die Gestalt der Erde-11 - Das harmonische Mittel
Die Gestalt der Erde-12 - Mittelwerte der Ellipse
Die Gestalt der Erde-13 - Mittelwerte und Erdgestalt

Es lassen sich die geographischen Minimal-Maximal-Grenzen ermitteln:

für 300 > n > 296 ==> 30° 08' 17,99" < Phi < 30° 08' 24,4"

Also beläuft sich die geographische Winkeldifferenz auf: Delta Phi = 6,41". Das entspricht einer Strecke von etwa 206,6 Meter.

D.h. die Hälften aller Mittelwerte für alle geodätischen Systeme (die bisher benutzt wurden), und damit auch für die tatsächlichen Abmaße der Erde, liegen in einem schmalen Streifen von etwa maximal 207 m. Der Mittelstreifen wird durch das harmonische Mittel gebildet.

Auf dieser Position liegt, im übrigen, auch Heliopolis. Die Position von Heliopolis wird, in der Regel, wir folgt aangegeben:

Phi = +30° 09' N
Lambda = +31°19' E

Die Werte für die obere und untere Grenze liegen bei etwa 4 Bogenminuten, jeweils zu beiden Seiten hin, vom harmonischen Mittel entfernt. Dies entspricht einer Strecke von 7,7 km.
Das gesamte Intervall zwischen oberer und unterer Grenze beträgt also 15,4 km.

Abbildung 1.7 - Die Mittelwerte in Ägypten

Seite: 0 1 2 3 4 5 6 7 a 8 a 9 a 10 a 11 a 12 a 13 a 14