GIZEH - GEODÄTISCHE ERKENNTNISSE
Copyright © Klaus Piontzik
| Um eine geometrische Analyse des
Gizeh-Plateaus vornehmen zu können, bedarf es möglichst
genauer Karten. Bei der Durchsicht der Karten, die im
Internet zu beziehen sind, ergab sich jedoch, dass die
meisten Karten falsch sind. Daher erfolgt hier eine Untersuchung von Gizeh-Karten bzgl. ihrer Genauigkeit. Dazu werden die Messdaten von Finders Petrie benutzt: 8.1.1 - Definitionen: Pyramidenabständey1 – Nord-Süd-Abstand Cheops-Chefren = 13 931.6 inch = 353,86264 mx1 – West-Ost-Abstand Cheops-Chefren = 13 165.8 inch = 334,41132 m y2 – Nord-Süd-Abstand Chefren-Mykerinos = 15 170.4 inch = 385,32816 m x2 – West-Ost-Abstand Chefren-Mykerinos = 9 450.2inch = 240,03508 y3 – Nord-Süd-Abstand Cheops-Mykerinos = y1 + y2 = 29 102.0 inch = 739,1908 m x3 – West-Ost-Abstand Cheops-Mykerinos = x1 + x2 = 22 616.0 inch = 574,4464 m
8.1.2 - Definitionen: Grundkantenlängen der PyramidenDie Abmessungen der Pyramiden in Gizeh gemäß Daten aus der Ägyptologie
8.1.3 - BasiskarteDie beiden Definitionen erlauben es eine erste Karte der Gizeh-Pyramiden zeichnen zu können. Die im Folgenden als Basiskarte bezeichnet wird. |
||||||||||||||||

| Abbildung 8.1 – Basiskarte der Gizeh-Pyramiden |
| Die Cheops-Pyramide
besitzt eine Steigung von 14:11. Die Frage ist ob die
Ägypter das 14:11 Verhältnis nicht nur für die
Cheops-Pyramide verwendet haben, sondern auch für die
Gestaltung des Gizeh-Plateau benutzt wurde. Legt man die Quadraturkonstruktionen 1 und 2 zusammen, so ergeben die Seiten der Quadraturdreiecke zwei charakteristische Winkel. |
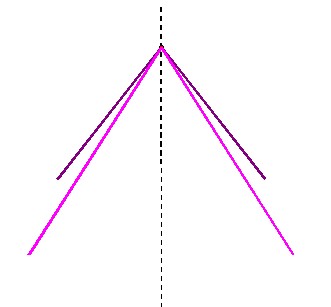
| Abbildung 8.2 – Winkel der Quadratur |
| Legt man an den Mittelpunkt der Cheops-Pyramide die Winkel aus den beiden Kreisquadraturen an, so ergibt sich folgendes Bild. |
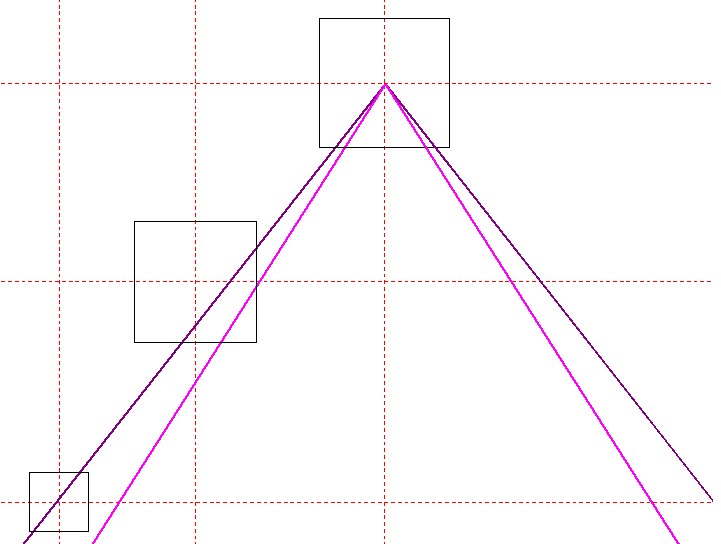
| Abbildung 8.3 – Quadraturwinkel in der Basiskarte des Gizeh-Komplexes |
| Aus der Basiskarte ergeben sich die Kriterien mit denen sich dir verzerrten Karten von den unverzerrten trennen lassen. |
8.2.1 - Kriterien zur Geometriebestimmung1) Der Mittelpunkt der Mykerinos-Pyramide liegt knapp unterhalb des 14:11 Winkel2) Der 14:11 Schenkel geht knapp an der süd-westliche Ecke der Mykerinos-Pyramide vorbei 3) Die Ostseite der Chefren-Pyramide geht etwa durch den Schnittpunkte des 11:7 Winkels mit der Waagerechten durch den Mittelpunkt der Chefren-Pyramide Damit lassen sich verzerrte Karten einwandfrei identifizieren und ausfiltern. |
| Es wird eine ältere Karte benutzt, und zwar die von Howard Vyse aus dem Jahr 1837. Die Karte zeigt den Gizeh-Komplex und das umliegende Gelände in einem Zustand, der noch relativ unberührt von Ausgrabungen war. Heißt also, dass nur die markantesten Bauwerke sichtbar sind, und sich daher für bestimmte Anschauungszwecke eine bessere Übersicht erzielen lässt. |
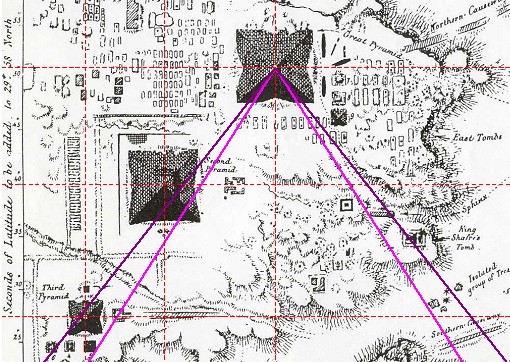
| Abbildung 8.4 – Quadraturwinkel in der Karte des Gizeh-Komplexes von Howard Vyse |
| Howard Vyse kam 1835 erstmals nach Ägypten und begann 1836 zusammen mit Giovanni Battista Caviglia mit Ausgrabungen in Gizeh. Nachdem er sich von Caviglia getrennt hatte, arbeitete er mit seinem neuen Assistenten John Shae Perring an der Erforschung der Pyramiden von Gizeh. Von John Perring stammt die folgende Karte des Gizeh-Komplexes. |
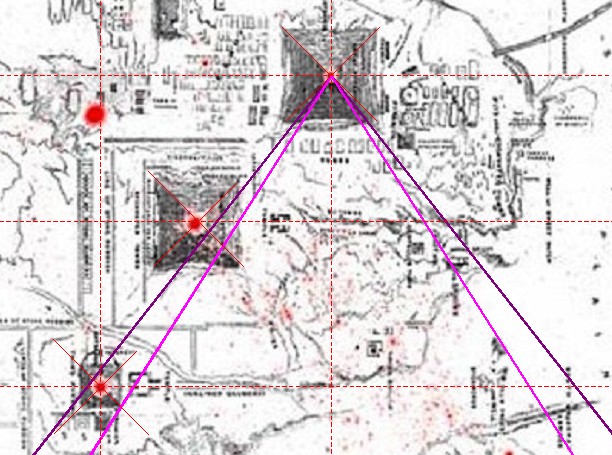
| Abbildung 8.5 – Quadraturwinkel in der Karte des Gizeh-Komplexes von John Perring |
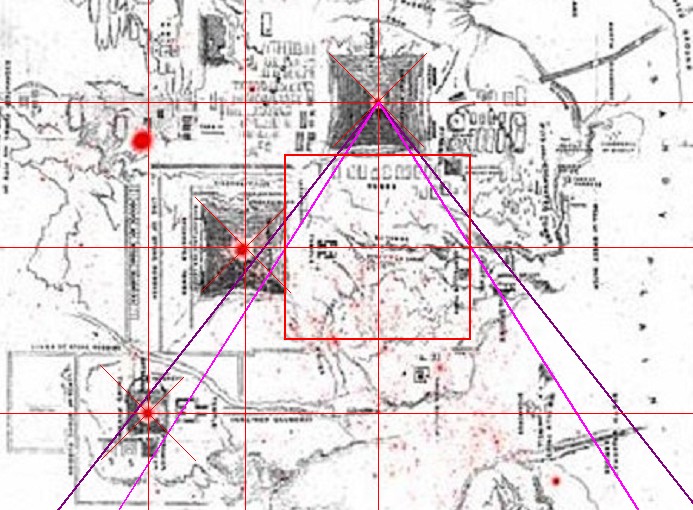
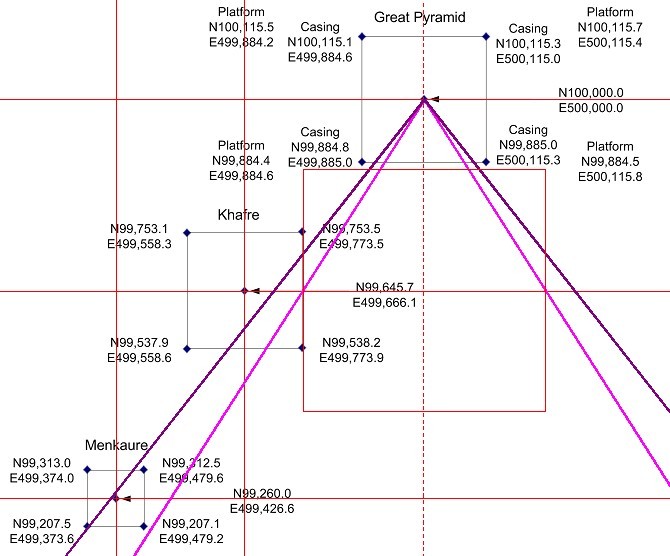
| Zwischen 1880 und 1883 tätigte Flinders Petrie seine Messungen am Gizeh Komplex. Daher existieren die ersten Daten über die Abstände der drei Pyramidenzentren voneinander. Weiterhin nahm er Messungen des Basisumfanges aller drei Pyramiden von Gizeh vor. |
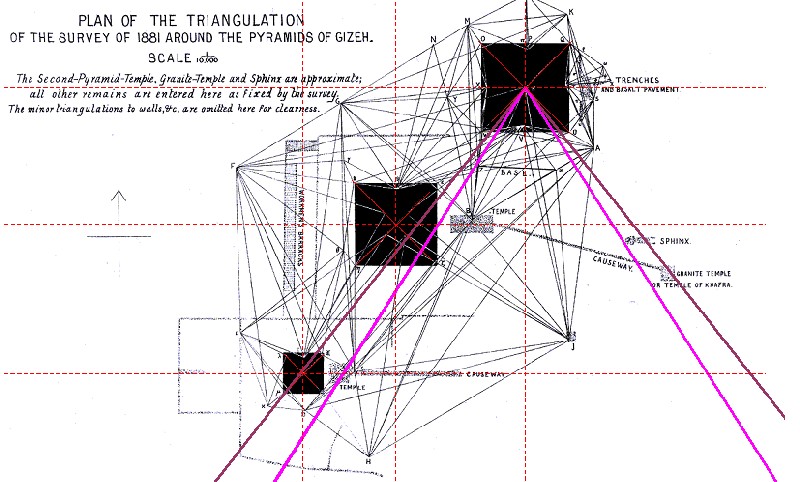
| Abbildung 8.6 – Quadraturwinkel in der Karte des Gizeh-Komplexes von Finders Petrie |
| Aus dem Jahr 2017 stammt die folgende Karte von Glen Dash, einem amerikanischen Ingenieur und Archäologen, der eigene Messungen in Gizeh gemacht hat. Die Karte beruht auf den Messwerten von Flinders Petrie, die in das Gizeh-Mapping-Project von Mark Lehner transformiert wurden. |
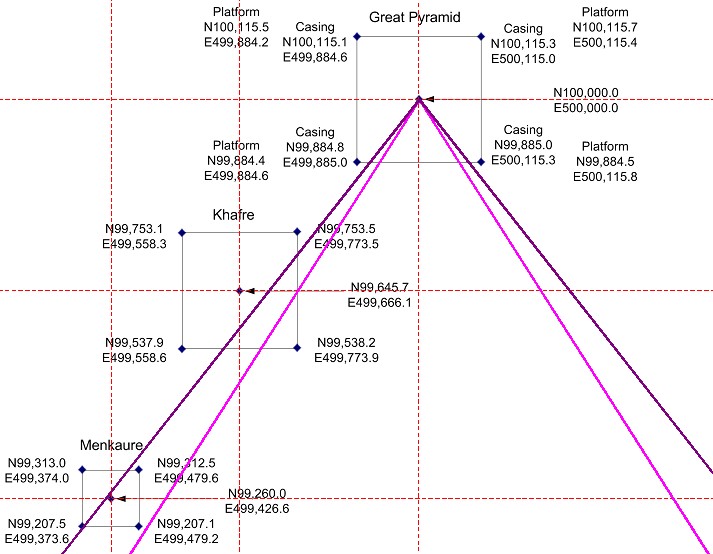
| Abbildung 8.7 – Quadraturwinkel in der Karte des Gizeh-Komplexes von Glen Dash |
| Die Angabe von Koordinaten erlaubt es, die Abstände der Pyramide zueinander zu ermitteln. Dabei zeigen sich Differenzen zu den Petrie-Messwerten. |
| Glen Dash | Flinders Petrie | Differenz | |
| y1-Cheops-Chefren | 354,3 m | 353,86 m | 0,44 m |
| x1-Cheops-Chefren | 333,9 m | 334,41 m | 0,51 m |
| y2-Chefren-Mykerinos | 385,7 m | 385,33 m | 0,37 m |
| x2-Chefren-Mykerinos | 239,5 m | 240,04 m | 0,54 m |
| Die Differenzen der Daten von Glen
Dash zu den Daten von Flinders Petrie betragen zwischen 0,37
- 0,54 m. Bei einer derartigen Differenz kann
man die Karte von Glen Dash zwar zu zeichnerischen
Zwecken verwenden, da hier die Zeichenungenauigkeit bei
0,1 mm = 1 m liegt. Für eine rechnerische Verwertung sind die Daten von Glen Dash aber nicht geeignet. |
| Insgesamt erweisen sich hauptsächlich die alten Karten des Gizeh-Plateaus noch als unverfälscht. Es werden daher in der weiteren Untersuchung die Karten von Howard Vyse, John Perring, Flinders Petrie und Glen Dash, sowie die Basiskarte benutzt. |
| Man sollte erwarten, dass die Karte
von Mark Lehner aus dem Giza-Mapping-Project genauer als
die alten Karten ist, aber das Gegenteil ist der Fall. Im Internet kursieren mehrere Varianten der Lehner-Karte. Alle zeigen die gleichen Abweichungen. |
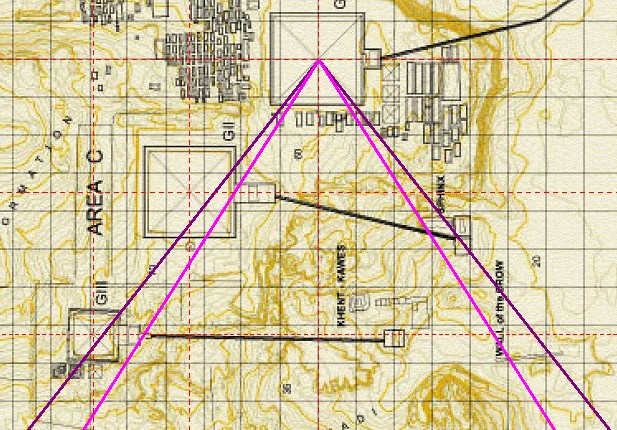
| Abbildung 8.8 – Quadraturwinkel in der Karte des Gizeh-Komplexes von Mark Lehner |
| Die Mykerinos-Pyramide liegt knapp
oberhalb des 14:11 Winkel Die Mykerinos-Pyramide ist nach Westen verschoben Auch die nächste, satellitengestützte Karte weist die gleiche Verzerrung auf, nämlich eine Streckung in Ost-West-Richtung |
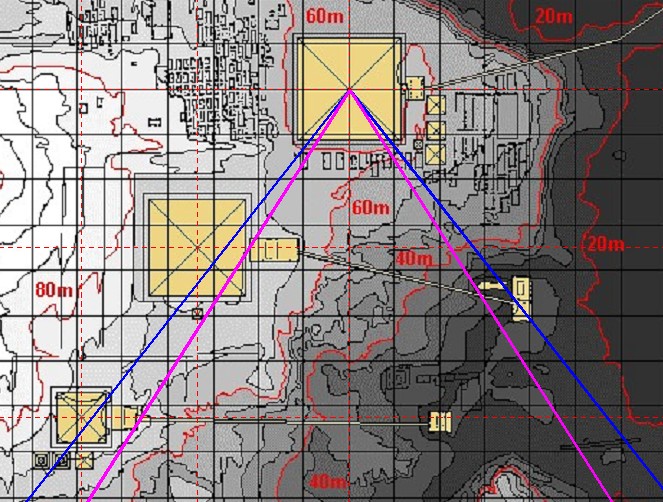
| Abbildung 8.9 – Quadraturwinkel in der Karte des Gizeh-Komplexes - Satellitengestützt |
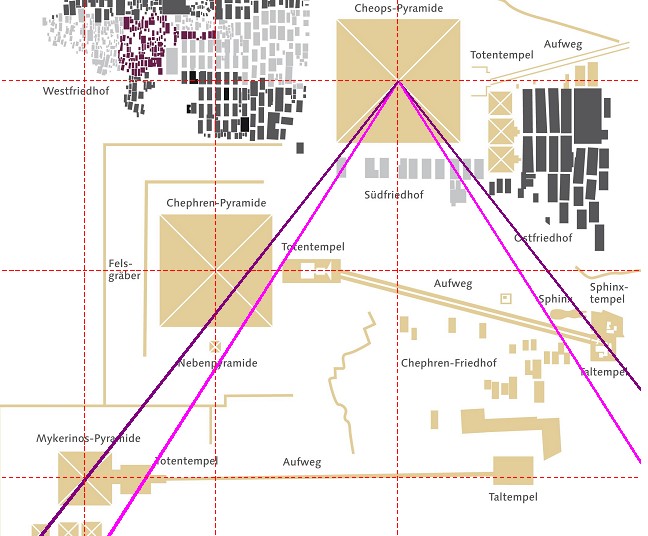
| Abbildung 8.10 – Quadraturwinkel in der Karte des Gizeh-Komplexes |
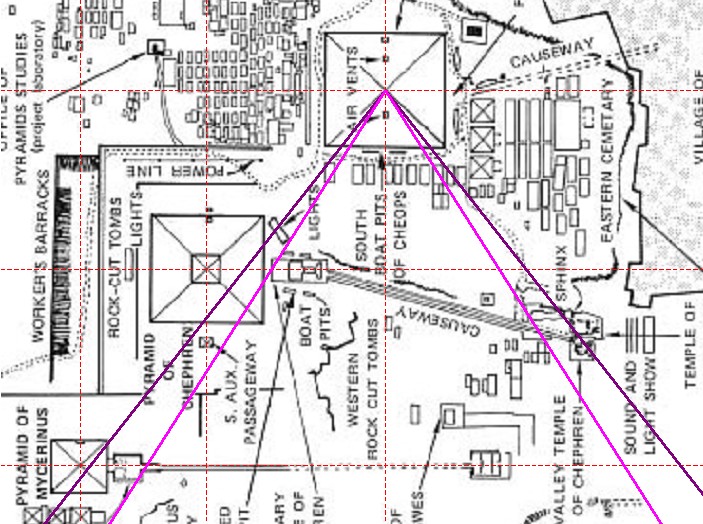
| Abbildung 8.11 – Quadraturwinkel in der Karte des Gizeh-Komplexes |
| Alle unter 8.4
gezeigten verzerrten Karten zeichnen sich durch folgende
Eigenschaften aus: Die Mykerinos-Pyramide liegt knapp oberhalb des 14:11 Winkel Die Mykerinos-Pyramide ist nach Westen verschoben Die Chefren-Pyramide ist leicht nach Westen verschoben Praktisch alle Karten des Gizeh-Plateaus, die im Internet erhältlich sind, verfügen über ähnliche Verzerrungen. Aus allen Karten ergibt sich: Die Sphinx liegt zwischen den östlichen Schenkeln der 14:11 und 11:7 Winkel. Die exakte Lage der Sphinx zwischen den östlichen 14:11 und 11:7 Schenkeln, sowie die Lage des Mykerinos-Komplexes zu dem 14:11 Schenkel und die Position der Chefren-Pyramide zum 11:7 Schenkel legen nahe, dass hier tatsächlich die 14:11 und 11:7 Proportion benutzt worden ist. |
| Die erste Quadratur die sich auf dem Gizeh-Plateau ergibt,
besteht aus den Schenkeln des 11:7 Winkels
und der Waagerechten die durch den Mittelpunkt
der Chefren-Pyramide verläuft. Diese Quadratur 2 wird in den folgenden Betrachtungen als Chefren-Quadratur bezeichnet. Höhe des Quadraturdreiecks = Abstand Cheops-Chefren-Pyramide = y1 = 11 Einheiten y1 = 353,86264 m = 11 Einheiten ==> 1 Einheit = 32,16933091 m Umquadrat = 14 Einheiten = 450,3706327 m Kreisradius = 7 Einheiten = 225,18531614 m |
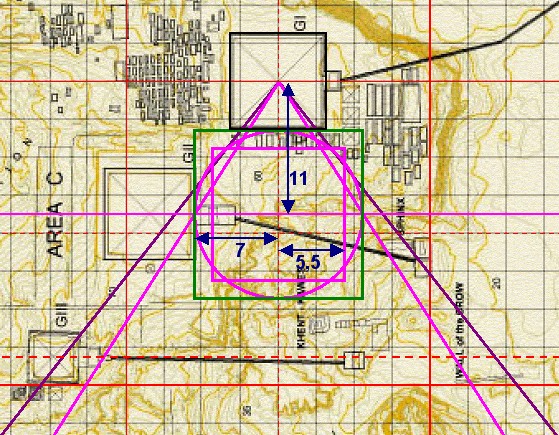
| Abbildung 8.12 – Die Chefren-Quadratur in der Karte des Gizeh-Komplexes von Mark Lehner |
| Die westliche Seite des Umquadrates der Chefren-Quadratur stimmt mit der Ostseite des Chefren-Komplexes überein. In den verschiedenen Karten sieht das folgendermaßen aus: |
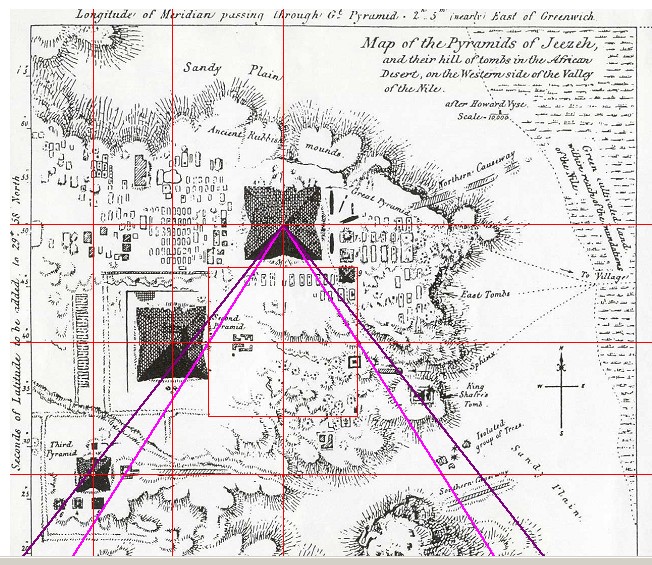
| Abbildung 8.13 – Umquadrat in der Karte des Gizeh-Komplexes von Howard Vyse |
| Abbildung 8.14 – Umquadrat in der Karte des Gizeh-Komplexes von John Perring |
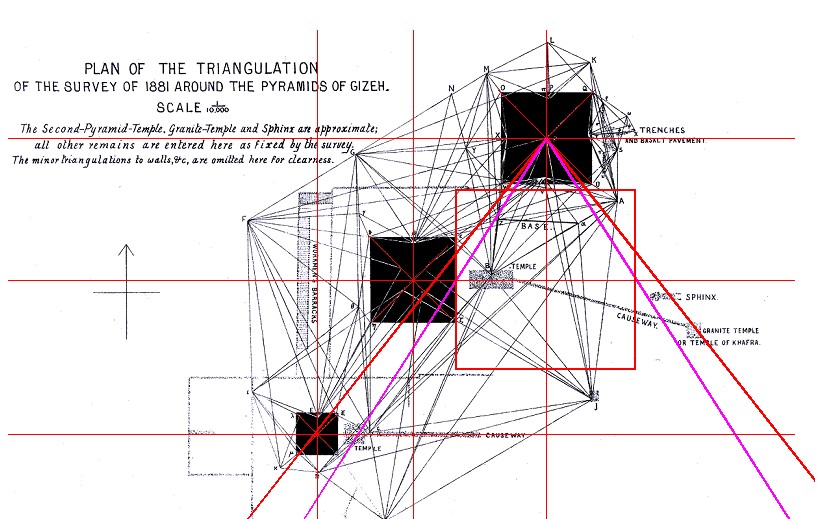
| Abbildung 8.15 – Umquadrat in der Karte des Gizeh-Komplexes von Finders Petrie |
| Abbildung 8.16 – Umquadrat in der Karte des Gizeh-Komplexes von Glen Dash |
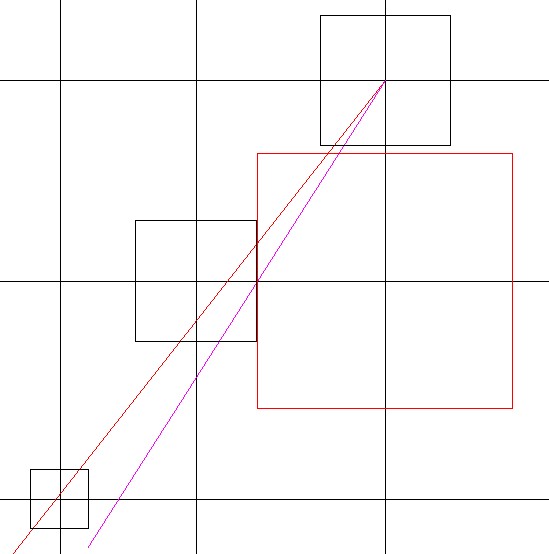
| Abbildung 8.17 – Umquadrat in der Basiskarte des Gizeh-Komplexes |
| Aus allen Karten
ergibt sich: Die westliche Seite des Umquadrates der Chefren-Quadratur bedingt die Ostseite des Chefren-Komplexes. |
| Zuerst werden die Größen
des Quadraturdreiecks ermittelt: y1 = 353,86264 m = 11 Einheiten mit 11:7 Verhltnis gerechnet: s = y1*7/11 = 225,1853164 m = 7 Einheiten mit pi/2 Verhltnis gerechnet s = 225,2759533 m Dann wird der Abstand bis zum Mittelpunkt der Chefren-Parymide berechnet: x1 = 334,41132 m mit 11:7 Verhltnis gerechnet: s1 = x1 - s = 109,2260036 m mit pi/2 Verhltnis gerechnet s1 = x1 - s = 109,1353667 Die Maße der Chefren-Parymide: OstWest-Seite: 215,25 m halbe Seite: s2 = 107,625 m Der Abstand der Chefren-Parymide zum Umquadrat: mit 11:7 Verhltnis gerechnet s1 - s2 = 1,601 m mit pi/2 Verhltnis gerechnet s1 - s2 = 1,5103 m Die westliche Seite des Umquadrates der Chefren-Quadratur besitzt einen Abstand von 1,6 Meter zur Ostseite der Chefren-Pyramide, wenn das 11:7 Verhältnis benutzt wird. Der Abstand beträgt 1,5103 Meter wenn das genaue Verhältnis pi/2 benutzt wird. |