 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
|
| 6.1.0 | Die Quadratur als Grundkonstruktion |
 |
 |
 |
 |
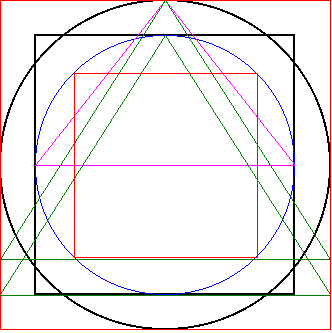Auf dieser Seite möchte ich einen
Zusammenhang zwischen Quadratur des Kreises und dem
Fünfeck zeigen. Ausgangspunkt ist dabei eine reduzierte
Version der Gesamtkonstruktion AB siehe Erweiterungen 1 |
|
 |
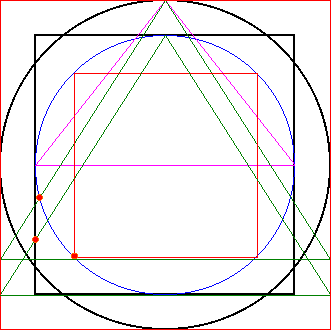In dieser Konstruktion sind schon
drei Punkte des Fünfecks annähernd enthalten. Es sind die rot markierten Punkte. Nun müssen noch die restlichen Punkte des Fünfecks ermittelt werden. |
| 6.1.1 | Schritt 1: Das Grundquadrat aus dem Quadraturdreieck 1 |
|
|
|
 |
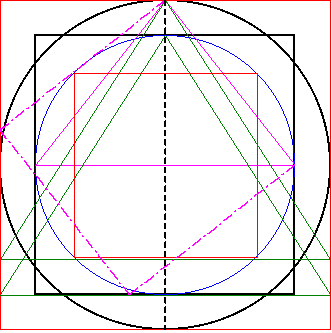Der erste Schritt besteht darin aus dem Quadraturdreieck 1 (magenta), dh. aus der rechten Seite des Dreiecks, ein Quadrat zu erzeugen. Ich werde dieses Quadrat in Zukunft als Grundquadrat bezeichnen. | |
 |
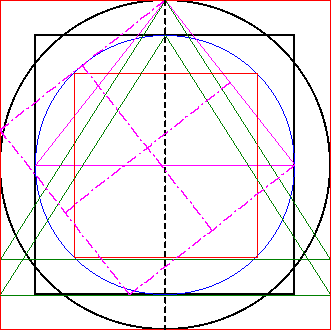In das Grundquadrat werden noch die Mittelsenkrechten der Quadratseiten eingezeichnet. So entstehen vier kleine Quadrate. |
| 6.1.2 | Schritt 2: Die Konstruktion der 1:2 Geraden |
|
|
|
 |
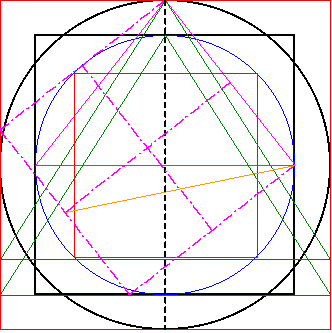Der zweite Schritt besteht darin in bzw. durch die vier kleinen Quadrate des Grundquadrates eine Gerade (orange) zu erzeugen, die eine Steigung von 1:2 (bzgl. des Grundquadrates) aufweist. | |
 |
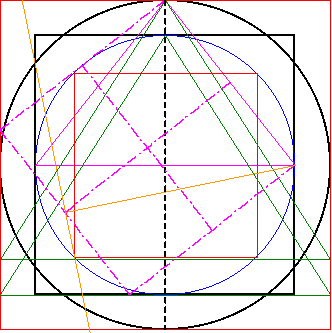Im linken Endpunkt der erzeugten Geraden wird dann noch die Senkrechte errichtet. |
| 6.1.3 | Schritt 3: Die Ermittlung des Fünfeck-Mittelpunktes |
|
|
|
 |
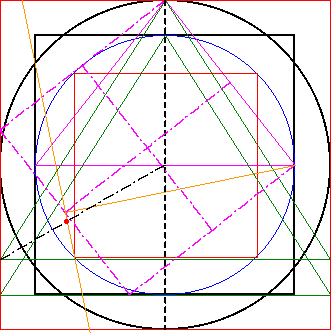Im dritten Schritt wird der Mittelpunkt des
Fünfecks erzeugt. Dazu wird der Mittelpunkt der Gesamtkonstruktion mit einer Ecke eines der Quadraturdreicke 2 verbunden. Der Schnittpunkt mit der erzeugten 1:2 Senkrechten ergibt den gesuchten Mittelpunkt. |
|
 |
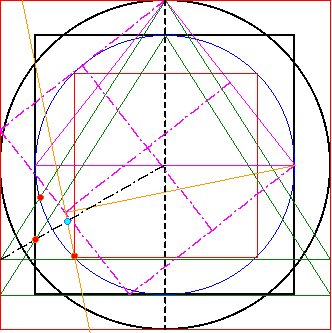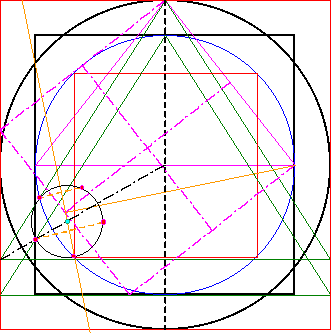
Hier ist der Mittelpunkt des Fünfecks
(zyan) noch einmal mit den bereits vorhandenen
Fünfeckpunkten (rot) eingezeichnet. Jetzt ist deutlich zu erkennen, das die 1:2 Senkrechte durch den Mittelpunkt und durch einen Fünfeckpunkt verläuft. Also ist sie eine Spiegelachse des Fünfecks |
| 6.1.4 | Schritt 4: Die Konstruktion des Fünfecks |
|
|
|
 |
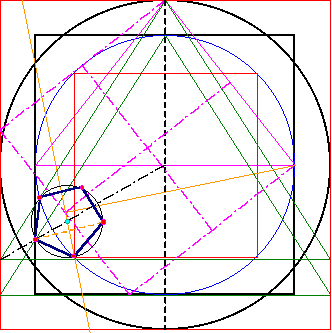
Da Mittelpunkt und drei Fünfeckpunkte
bekannt sind, lässt sich der Umkreis des Fünfecks
erzeugen. Durch Spiegelung werden die restlichen Punkte des Fünfecks ermittelt |
|
 |
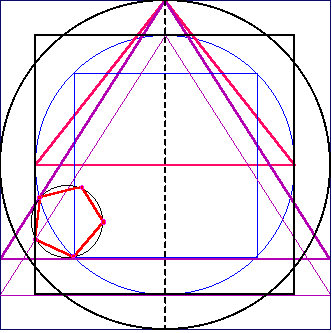
Verbinden aller Punkte erzeugt schließlich das Fünfeck |
| Da die Gesamtkonstruktion symmetrisch ist, lässt sich noch ein zweites Fünfeck erzeugen, und zwar auf der rechten Seite der Gesamtkonstruktion. |
| 6.1.5 | Die minimierte Quadratur mit Fünfeck |
|
|
|
 |
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
