 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
|
| 5.1.0 | Die Quadratur des Kreises - Konstruktion 3 |
 |
 |
 |
| Bis jetzt haben wir nur Konstruktionen
betrachtet,die zueinander umfangsgleiche Quadrate und
Kreise enthalten. Unter der Qudratur des Kreises kann man aber auch die Umwandlung eines Kreises in ein flächengleiches Quadrat verstehen. |
| Kreis und Quadrat besitzen gleichen Flächeninhalt: |
|
| Es ergibt sich folgendes Verhältnis für den Radius/Durchmesser zur Quardatseite: |
 |
 |
| 5.1.1 | Die Entwicklung aus der Quadratur 1 |
|
|
|
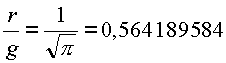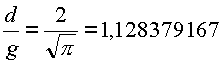| Die flächengleiche Quadratur des Kreises kann man aus der Kreisquadratur 1 ableiten. | |
| Voraussetzung : |  |
| Für die Kreisfläche gilt dann: |  |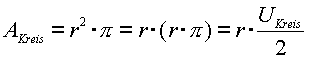
 |
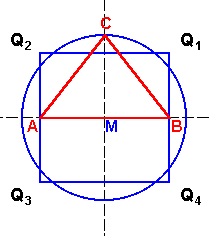Die Quadratur des Kreises 1 kann im Wesentlichen so dargestellt werden: |
 |
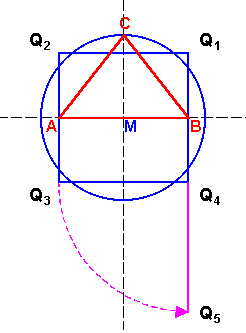Das Quadrat ist umfangsgleich zum Kreis,
also gilt:
Die Strecke Q1Q5 entspricht dabei dem halben Kreisumfang |
| 5.1.2 | Ein flächengleiches Rechteck |
|
|
|
 |
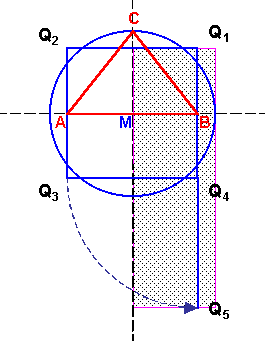Für die Kreisfläche gilt insgesamt dann:
Das schraffierte Rechteck entspricht also der Kreisfläche |
| 5.1.3 | Eine weitere Flächengleichheit |
|
|
|
 |
 |
| 5.1.4 | Das flächengleiche Quadrat |
|
|
|
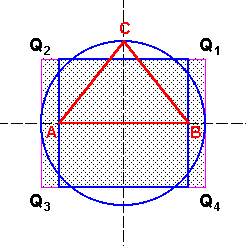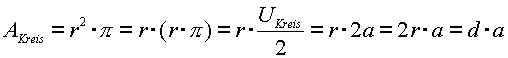| Bis hierhin ist es also gelungen, ein dem Kreis entsprechendes, flächengleiches Rechteck aus der Kreisquadratur 1 abzuleiten. |
AKreis = AQuadrat
AQuadrat= g2 = d*a
| Dieses Rechteck wird nun in ein flächengleiches Quadrat transformiert. Dies kann nach verschiedenen Methoden geschehen. Hier bietet sich der Höhensatz des Euklid an. |
 |
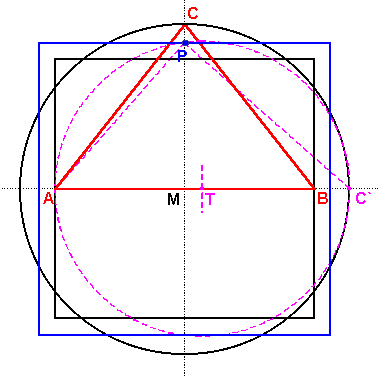Hier braucht nicht mit
den ganzen Strecken a
und d gearbeitet zu werden. Man kommt mit den
halben Seiten aus. Die
Strecke AC' wird halbiert. Es ensteht der
Halbierungspunkt T. Um T
wird ein Kreis gezogen und zwar mit derStrecke TC'
als Radius. |
| Abbildung 14 - Die Quadratur 3 |
| Somit steht eine Technik zur Verfügung, die es gestattet einen Kreis in ein flächengleiches Quadrat, auf geometrischem Wege, zu transformieren. |
| 5.1.5 | Weitere Beziehungen |
|
|
|
| Zwischen flächengleichem Quadrat, dem Kreis und dem umfanggleichen Quadrat existiert noch ein interessanter Zusammenhang: |
| Die Seite aus dem flächengleichen Quadrat
ist geometrisches
Mittel zwischen dem Kreisdurchmesser und der Seite
des umfanggleichen Quadrats. Damit lässt sich die gesamte Beziehung so darstellen: |
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
