 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 4.1.0 | Die Grundkonstruktion | |
| 4.1.1 | Die Erweiterung durch Quadrate | |
| 4.1.2 | Die Erweiterung durch Kreise | |
| 4.1.3 | Die Zusammenfasung | |
| 4.1.4 | Die Gesamtkonstruktion A | |
| 4.1.5 | Die Gesamtkonstruktion B | |
| 4.1.6 | Die Gesamtkonstruktion AB | |
| 4.1.7 | Die Gesamtkonstruktion C | |
|
| 4.1.0 | Die Grundkonstruktion |
 |
 |
 |
| Es existieren Publikationen, wie John
Michells Buch "Maßsysteme der Tempel", in
denen die Quadratur-Konstruktion um entsprechende Um-
und Inkreise bzw. Um-
und Inquadrate erweitert wird. Ausgangspunkt ist immer ein Kreis und ein Quadrat, die den gleichen Umfang besitzen. Beide sind in der Regel symmetrisch zu einem gemeinsamen Mittelpunkt M angeordnet. Im folgenden einfach Grundkonstruktion genannt. |
 |
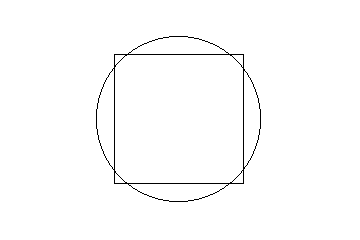Abbildung 5a - Grundkonstruktion
| 4.1.1 | Die Erweiterung durch Quadrate |
|
|
|
| Geht man vom Kreis aus, so lassen sich zum umfangsgleichen Quadrat noch zwei andere Quadrate erzeugen. Nämlich das Inquadrat und das Umquadrat des Kreises. Das sieht dann so aus: |
 |
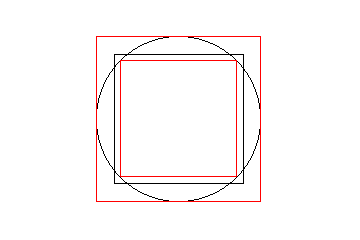Abbildung 5b - Erweiterung durch Quadrate
| 4.1.2 | Die Erweiterung durch Kreise |
|
|
|
| Umgekehrt kann man auch von dem Quadrat ausgehen, und auch hier findet man neben dem umfangsgleichen Kreis, noch zwei weitere Kreise. Den Umkreis und den Inkreis des Quadrates. |
 |
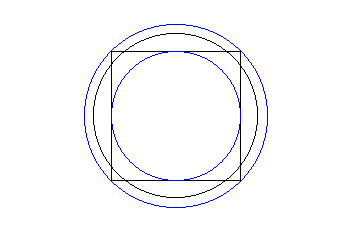Abbildung 5c - Erweiterung durch Kreise
| 4.1.3 | Die Zusammenfassung |
|
|
|
| Die in Abbildung 5 a bis c erzeugten Kreise und Quadrate lassen sich auch zu einer einzigen Konstruktion zusammen fassen. |
 |
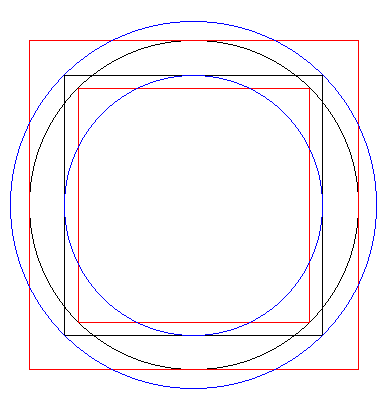Abbildung 6 - Zusammenfassung der Kreise und Quadrate
| 4.1.4 | Die Gesamtkonstruktion A |
|
|
|
| Üblicherweise wird diese Zusammenfassung dann noch durch die beiden Quadratur-Dreiecke ergänzt, so daß sich jetzt, im folgenden Gesamtkonstruktion A genannt, ergibt: |
 |
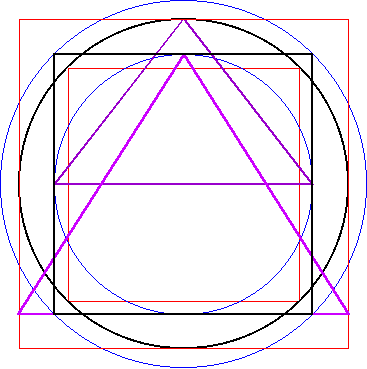Abbildung 7 - Gesamtkonstruktion A
| 4.1.5 | Die Gesamtkonstruktion B |
|
|
|
| Eine etwas andere Art der Zusammenfassung entsteht, wenn die beiden Quadratur-Dreiecke mit ihren Spitzen zusammen gelegt werden. |
 |
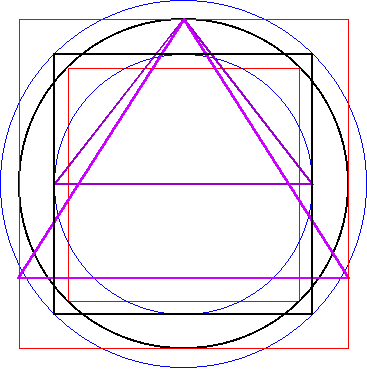Abbildung 8a - Vorstufe Gesamtkonstruktion B
| Ergänzt man die Abbildung 8a noch durch ein Innen- und ein Aussen-Quadrat, so entsteht die Gesamtkonstruktion B. |
 |
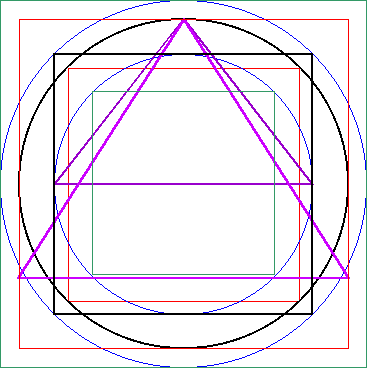Abbildung 8b - Gesamtkonstruktion B
| 4.1.6 | Die Gesamtkonstruktion AB |
|
|
|
| Weiterhin lassen sich die Konstruktion A und die Konstruktion B zu einer einzigen Figur zusammensetzen. Es ergibt sich die Gesamtkonstruktion AB. |
 |
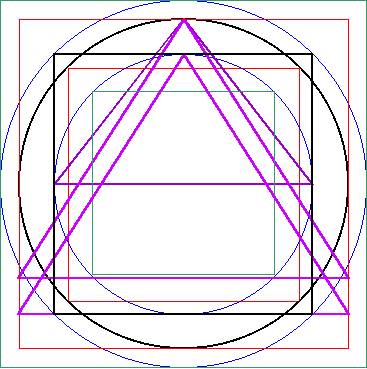Abbildung 9 - Gesamtkonstruktion AB
| 4.1.7 | Die Gesamtkonstruktion C |
|
|
|
| Schließlich lässt sich die Konstruktion AB noch durch die Erweiterung des Quadraturdreiecks 1 ergänzen. Es ergibt sich die Gesamtkonstruktion C. |
 |
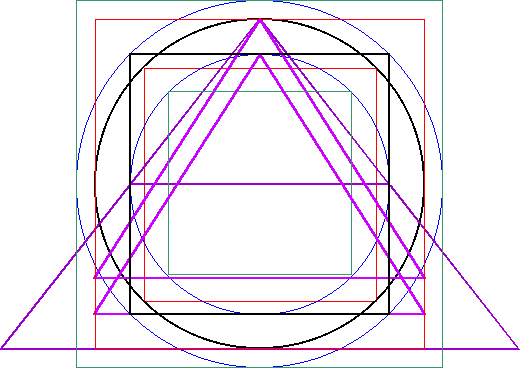Abbildung 10 - Gesamtkonstruktion C
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
