DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG

Quadratur und Fünfeck 2

Die Ruhr - Konstruktion

6.2.0		Die Quadratur AB als Grundkonstruktion
6.2.1		Schritt 1: Das Quadrat aus dem Quadraturdreieck 1
6.2.2		Schritt 2: Die Konstruktion der 1:2 Geraden
6.2.3		Schritt 3: Die Sechseck-Konstruktion
6.2.4		Schritt 4: Die Ermittlung des Fünfeck-Mittelpunktes
6.2.5		Schritt 5: Die Konstruktion des Fünfecks
6.2.6		Die Gesamtkonstruktion
6.2.7		Die essentielle Gesamtkonstruktion

zurück

Verzeichnis

Home

weiter

6.2.0

Die Quadratur als Grundkonstruktion

Auf dieser Seite möchte ich einen Zusammenhang zwischen der Quadratur des Kreises, dem Sechseck und dem Fünfeck zeigen. Die Gesamtkonstruktion die sich dabei ergibt stellt, für heutige Begriffe, eine mathematische Premiere dar.

Ausgangspunkt ist dabei eine reduzierte Version der Gesamtkonstruktion AB aus Erweiterungen 1.

6.2.1

Schritt 1: Das Quadrat aus dem Quadraturdreieck 1

Der erste Schritt besteht darin aus dem Quadraturdreieck 1 (magenta), dh. aus der rechten Seite des Dreiecks, ein Quadrat zu erzeugen, wie in Erweiterungen 2.

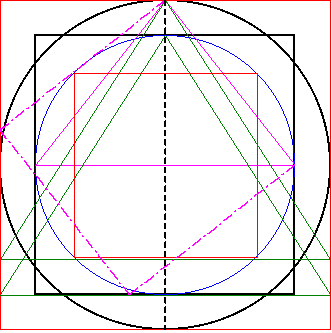In dieses Grundquadrat werden noch die Mittelsenkrechten der Quadratseiten eingezeichnet. So entstehen vier weitere kleine Quadrate.

Das Grundquadrat ist erweiterbar. Man kann daraus ein konplettes Gittersystem generieren.

6.2.2

Schritt 2: Die Konstruktion der 1:2 Geraden

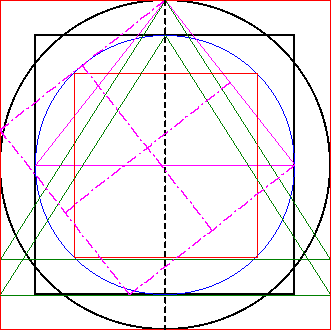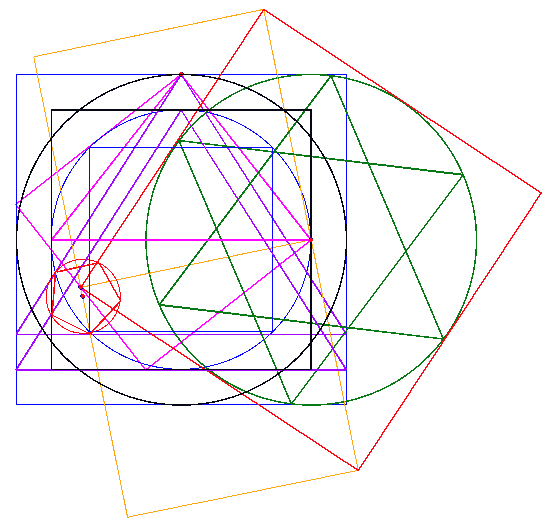
Der zweite Schritt besteht darin in bzw. durch die vier kleinen Quadrate des Grundquadrates eine Gerade (orange) zu erzeugen, die eine Steigung von 1:2 (bzgl. des Grundquadrates) aufweist.

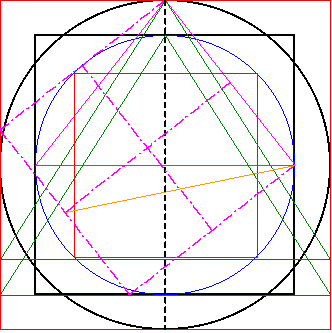Im linken Endpunkt der erzeugten Geraden wird noch die Senkrechte errichtet.

Aus diesen 1:2-Geraden lässt sich ebenfalls ein Quadrat und daraus wiederum ein Gitter erzeugen, das sogenannte 1:2-Gitter.

6.2.3

Schritt 3: Die Sechseck-Konstruktion

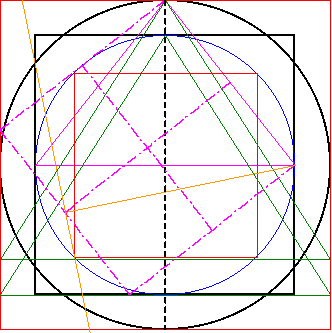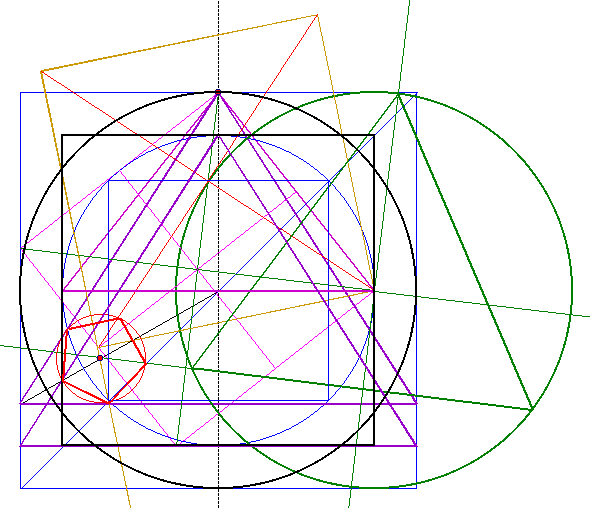
Im dritten Schritt wird das Sechseck bzw. der Sechserstern erzeugt.

Dazu werden die Diagonalen des Grundquadrates (grün) benutzt.
Die Diagonalen stehen senkrecht aufeinander und werden als Diagonalsystem bezeichnet.

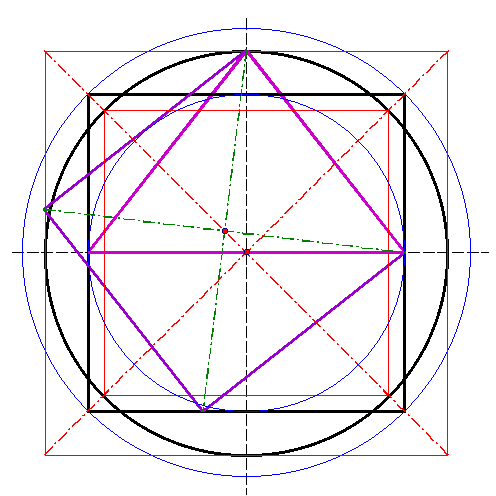In der rechten Ecke des Quadraturdreicks 1 wird das Diagonalsystem eingezeichnet.

Der Dreieckspunkt ist der Mittelpunkt der Sechseck-Konstruktion.

Um den Dreieckspunkt wird der Quadraturkreis eingetragen, sowie der Umkreis und der Inkreis des Qaudraturquadrates.

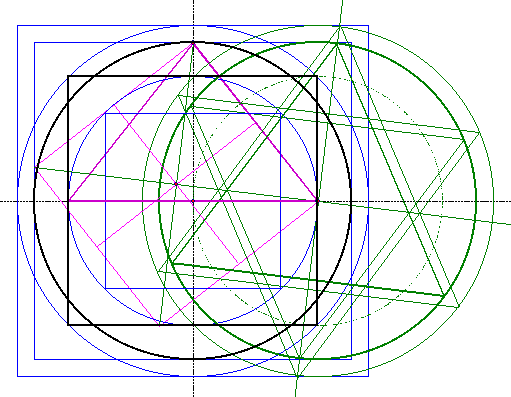
Die Senkrechte aus dem Diagonalsystem, die durch die rechte Ecke des Quadraturdreicks 1 verläuft, ist eine Symmetrieachse des Sechsecks.

Mit der Symmetrieachse lassen sich, in den beiden äußeren Kreisen, die Sechsersterne erzeugen.

6.2.4

Schritt 4: Die Ermittlung des Fünfeck-Mittelpunktes

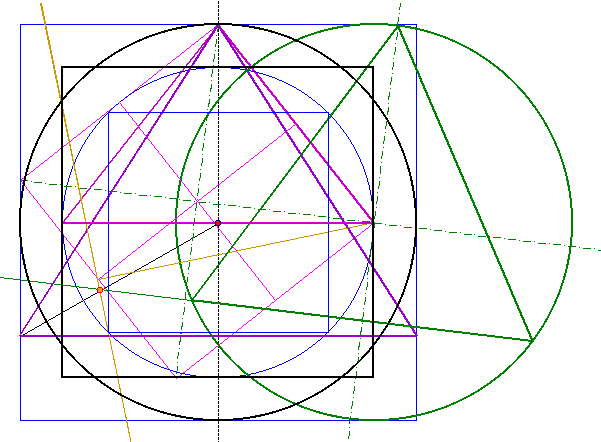
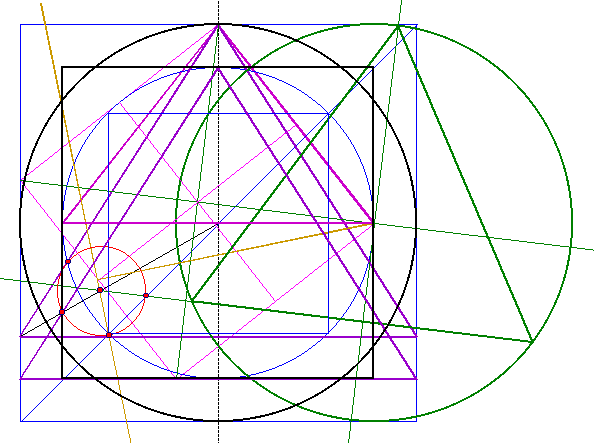
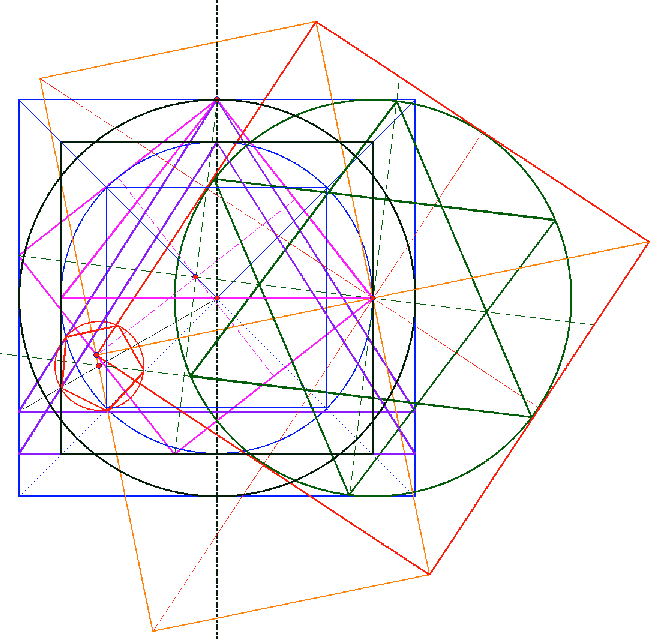
Im vierten Schritt wird der Mittelpunkt des Fünfecks ermittelt.
Dazu wird der Mittelpunkt der Gesamtkonstruktion mit der linken Ecke des Quadraturdreicks 2 verbunden.
Weiterhin wird die untere Seite des Dreiecks aus der Sechsecks-Konstruktion verlängert.
Der Schnittpunkt der zwei erzeugten Geraden mit der 1:2 Senkrechten ergibt den gesuchten Mittelpunkt.