 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 8.1.0 | Die Cheops-Pyramide und die Quadratur | |
| 8.1.1 | Die Quadraturbedingung | |
| 8.1.2 | Die Neigungswinkel der Pyramide | |
| 8.1.3 | Der Vergleich der Winkel | |
| 8.1.4 | Cheops-Pyramide und Quadraturdreieck 1 | |
|
| 8.1.0 | Die Cheops Pyramide und die Quadratur |
 |
 |
 |
 |
Es wird
des öfteren behauptet, die Cheops-Pyramide sei ein
architektonischer Ausdruck für die Quadratur des
Kreises. Das wird aus dem Neigungswinkel der Seiten geschlossen, die in der Nähe des Quadraturwinkels für die Quadraturkonstruktion 1 liegen. |
| 8.1.1 | Die Quadraturbedingung |
|
|
|
 |
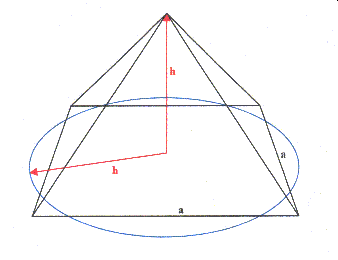U = UKreis = UQuadrat U = 2πr = 4a Der Radius der Kreises ist gleich der Höhe der Pyramide: U = 2πh = 4a |
| 8.1.2 | Der Neigungswinkel der Pyramide |
|
|
|
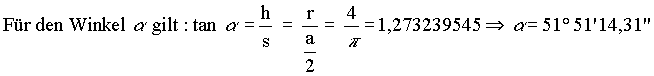
| Der Umstand läßt sich vereinfachen, wenn für pi eine Näherung benutzt wird. Die einfachste Annäherung an π ist die Anwendung eines Teiles der archimedischen Ungleichung: |
 |
| 8.1.3 | Der Vergleich der Winkel |
|
|
|
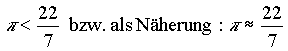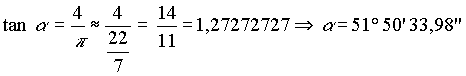
| In seinem 1997 veröffentlichtem Buch "Das erste Weltwunder" gibt Mark Lehner auf Seite 17 einen Wert von 51° 50' 40'' für den Neigungswinkel der Cheops-Pyramide an. |
| exakterWert: | 51° 51' 14,31'' |
| Näherungswert: | 51° 50' 33,98'' |
| Die Differenz des
tatsächlichen Wertes (Lehner) mit der exakten Quadratur
beträgt etwa eine Bogenminute, während die Differenz
zur Näherungslösung nur 6 Bogensekunden ausmacht. Die Konsequenz ist, das die Cheopspyramide mit der 14:11 Proportion gebaut worden ist, und nicht mit dem exakten Quadraturwert pi/4. Und das sagt noch gar nichts darüber aus, ob die Ägypter nur die 14:11-Proportion gesehen haben, oder ob sie von dem tatsächlichen Wert Kenntnis hatten. |
| Mark Lehner gibt in seinem Buch die
Steigungswinkel weiterer Pyramiden an. Dort lassen sich
noch zwei Pyramiden finden, die die 14:11-Proportion
benutzen: Snofru (Meidum) und Niuserre (Abusir) mit 51° 50' 35'' Die Differenz des
tatsächlichen Wertes zur Näherungslösung beträgt nur 1
Bogensekunde |
| 8.1.4 | Cheops Pyramide und Quadraturdreieck 1 |
|
|
|
 |
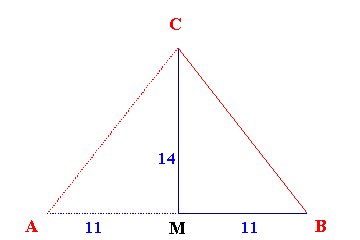Nimmt man ein rechtwinkliges Dreieck, (in
der Abbildung die Dreiecke MBC bzw. MAC) mit dem Höhen/Seiten -
Verhältnis 14:11, so läßt sich
daraus erst das Quadraturdreieck und anschließend die
komplette Quadratur 1 ableiten. Schneidet man die Cheopspyramide in Nord-Süd oder Ost-West-Richtung durch, so erhält man als Schnittfigur das Dreieck ABC. Des öfteren werden Quadraturdreiecke daher auch als Cheopspyramiden bezeichnet. |
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
