DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 1.4.0 | Definition der Quadratur des Kreises | ||
| 1.4.1 | Zur Vorgeschichte der Quadratur des Kreises | ||
| 1.4.2 | Die Verbindung Ägypten-Griechenland | ||
| 1.4.3 | Die Hinwendung zur Geometrie | ||
| 1.4.4 | Anaxagoras | 499-428 v. Chr. | |
| 1.4.5 | Hippokrates von Chios | 450 v. Chr | |
| 1.4.6 | Hippias von Elis | 5. Jh v. Chr. | |
| 1.4.7 | Antiphon | 5. Jh v. Chr | |
| 1.4.8 | Bryson von Herakleia | 450 - 390 v. Chr. | |
| 1.4.9 | Eudoxos | 410 - 347 v. Chr. | |
| 1.4.10 | Deinostratus | 390 - 320 v. Chr. | |
| 1.4.11 | Euklid | 360 - 280 v. Chr. | |
| 1.4.12 | Nikomedes | 280 - 210 v. Chr. | |
| 1.4.13 | Archimedes | 287 - 212 v.Chr. | |
| Die Quadratur des Kreises wird als ein
klassisches Problem der Geometrie bezeichnet und lässt
sich in zwei Teilaufgaben einteilen. 1) der so genannten Rektifikation des Kreises, also der Konstruktion einer geraden Strecke, die dem Kreisumfang entspricht 2) aus einem gegebenen Kreis ein Quadrat mit demselben Flächeninhalt zu konstruieren Werden die Konstruktionsmittel auf Lineal und Zirkel beschränkt, ist die Aufgabe unlösbar. Dies konnte jedoch erst im Jahr 1882 vom deutschen Mathematiker Ferdinand von Lindemann bewiesen werden. Die Quadratur des Kreises gehört mit zu den populärsten Problemen der Mathematik. Jahrhundertelang suchten neben Mathematikern auch immer wieder Laien vergeblich nach einer Lösung. Der Begriff „Quadratur des Kreises“ ist daher in vielen Sprachen zu einer Metapher für eine unlösbare Aufgabe geworden. |
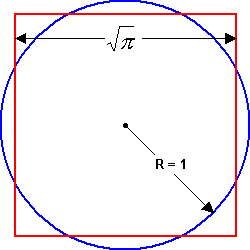 |
| Quadratur am Einheitskreis |
| Bereits in den alten Hochkulturen gab es Verfahren zur Berechnung von Kreisflächen. In der 48ten Aufgabe des Papyrus Rhind (um 1650 v. Chr.) wird als Fläche des Kreises vom Durchmesser 9 das Quadrat der Seitenlänge 8 angegeben, was einem recht genauen Wert für die Kreiszahl π von 256/81 = 3,16… entspricht. |
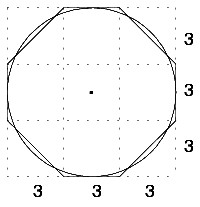 |
| Derartige Musterlösungen wurden aus der
Praxis gewonnen und waren für die Praxis bestimmt. Es
gab keine weitergehenden theoretischen Überlegungen,
insbesondere wurde kein Unterschied zwischen exakter
Lösung und Näherung gemacht. Eine deduktive Vorgehensweise in der Mathematik, bei der durch Beweise gestützte Sätze die Musteraufgaben ersetzen, entwickelte sich erst ab dem 6. Jahrhundert v. Chr. in Griechenland. |
Cheops-PyramideEinerseits ist durch entsprechende Papyrusfunde historisch nachgewiesen, dass auf dem Gebiet der Algebra den Ägyptern die vier Grundrechenarten und das Lösen von Gleichungen mit einer Unbekannten vertraut waren.In der Geometrie kannten sie die Berechnung der Flächen von Dreiecken, Rechtecken und Trapezen, sowie die Berechnung von Volumen, u.a. eines quadratischen Pyramidenstumpfes. Andererseits ist da die heute noch vorhandene Architektur, in Form der Pyramiden, Tempel und Statuen. Diese stellen ein steinernes Zeugnis der darin verwendeten Mathematik dar. |
 |
Die Cheops-Pyramide ist die älteste und größte der drei Pyramiden von Gizeh und wird auch als die Große Pyramide bezeichnet. Die Fertigstellung des Bauwerks wird auf 2580 v. Chr. in die Zeit des Alten Reiches datiert und dem ägyptischen Pharao Chufu zugesprochen, der weitaus bekannter unter seinem griechischen Namen Cheops geworden ist. |
Die Pyramide besitzt
eine quadratische Basisfläche, Ihre ursprüngliche
Seitenlänge wird auf 230,33 m (ca. 440 Königsellen)
geschätzt. Die Seitenlänge heute beträgt noch ca. 225
m.Die ursprüngliche Höhe wird auf 146,59 m (ca. 280
Königsellen) geschätzt. Da sie in späterer Zeit als
Steinbruch diente, beträgt ihre Höhe heute noch 138,75
m. Das Volumen ergibt sich zu 2.583.283 m3.
Die Quadratur in der PyramideAusgangspunkt ist die quadratische Basisfläche der Pyramide. Der Kreis der den gleichen Umfang wie das Quadrat besitzt, bestimmt mit seinem Radius auch die Höhe der Pyramide. |
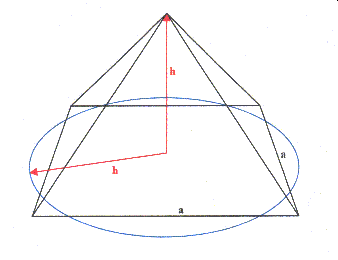 |
Der Umfang des Kreises ist
gleich dem Umfang der Pyramide: U = UKreis = UQuadrat U = 2π · r = 4a Der Radius der Kreises ist gleich der Höhe der Pyramide: U = 2π · h = 4a |
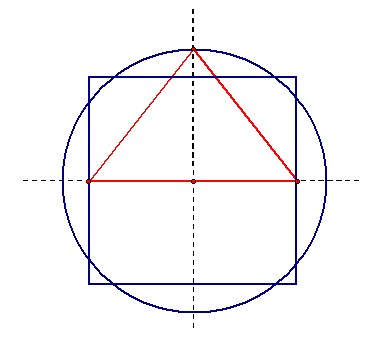 |
Die einfache wie auch geniale Idee war Kreis
und Quadrat mit einem Dreieck zu
verbinden. Und zwar so dass die Höhe des Dreiecks gleich dem Radius des Kreises und die Basisseite des Dreiecks gleich der Quadratseite ist. |
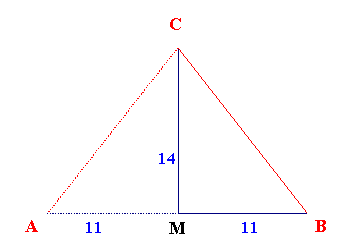 |
Nimmt man ein rechtwinkliges Dreieck, (in
der Abbildung die Dreiecke MBC bzw. MAC)
mit dem Höhen/Seiten - Verhältnis 14:11,
so läßt sich daraus erst das Quadraturdreieck und
anschließend die komplette Quadraturkonstruktion
1 ableiten. Schneidet man die Cheopspyramide in
Nord-Süd oder Ost-West-Richtung durch, so erhält man
als Schnittfigur das Dreieck ABC. |
SteigungswinkelDer Winkel im Punkt A und B ist der Steigungswinkel alphaFür den genauen Steigungswinkel gilt: |
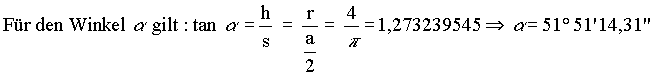
| Der Umstand läßt sich vereinfachen, wenn
für π eine Näherung benutzt wird. Die
einfachste Annäherung an π ist die Anwendung von π
= 22/7. Für den genäherten Steigungswinkel gilt: |
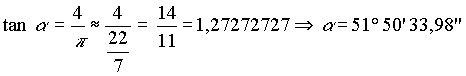
| In seinem 1997 veröffentlichtem Buch "Das erste Weltwunder" gibt Mark Lehner auf Seite 17 einen Wert von 51° 50' 40'' für den Neigungswinkel der Cheops-Pyramide an. |
| exakterWert: | 51° 51' 14,31'' |
| Näherungswert: | 51° 50' 33,98'' |
| Lehner | 51° 50' 40'' |
| Die Differenz des
tatsächlichen Wertes (Lehner) mit der exakten Quadratur
beträgt etwa eine Bogenminute, während die Differenz
zur Näherungslösung nur 6 Bogensekunden ausmacht. Die Konsequenz ist, dass die Cheopspyramide mit der 14:11 Proportion gebaut worden ist, und nicht mit dem exakten Quadraturwert π/4. Und das sagt noch gar nichts darüber aus, ob die Ägypter nur die 14:11-Proportion gesehen haben, oder ob sie von dem tatsächlichen Wert für π Kenntnis hatten. |
| Ein weiterer Anhaltspunkt für das 14:11
Verhältnis ergibt sich aus der Existenz zweier anderen
Pyramiden, deren Steigungswinkel Mark Lehner (und auch
ältere Quellen) mit 51° 50' 35''.
angibt. Snofru (Meidum) und Niuserre (Abusir). Siehe dazu auch: Cheopspyramide |
| Die Griechen
werden heute noch oft als die Erfinder der Mathematik
dargestellt. Dies ist so nicht ganz richtig. Die
griechische Mathematik ist nicht aus dem Nichts
entstanden, sondern geht aus dem Fundus der
damals bekannten Konstruktionen und
Überlegungen der Antike (also Ägypten und
Zweistromland) hervor. Eine Reihe griechischer Mathematiker, am bekanntesten sind Thales (624-546 v. Chr.) und Pythagoras (570-510 v. Chr.), reisten nach Ägypten und ins Zweistromland um sich dort in die Mathematik überhaupt erst einweisen zu lassen. Also etwa 1000 Jahre nach Papyrus Moskau und Rhind ! Die Konstruktion des (Thales)Kreises über einem rechtwinkligen Dreieck war sowohl den Ägyptern als auch den Babyloniern schon bekannt. Erst Thales erkannte die Allgemeinheit der Konstruktion und bewies sie auch. Daher sprechen wir heute vom Halbkreis bzw. vom Satz des Thales. Die Babyloniern besaßen Keilschrifttafeln mit Listen von sogenannten pythagoräischen Zahlen, also Zahlentripel durch die ein rechtwinkliges Dreieck bestimmt ist. Aus Ägypten stammt die sogenannte Zwölf-Knoten-Schnur, die entsprechend gefaltet (3:4:5) ein rechtwinkliges Dreieck bildet und in der Landvermessung benutzt wurde. Aber erst Pythagoras erkannte die Essenz in der Konstruktion und den Zahlenverhältnissen. Er war der erste der diese Beziehungen auch allgemein beweisen konnte. Daher sprechen wir heute vom Satz des Pythagoras. Die griechischen Mathematiker schöpften aus dem reichhaltigen Fundus der bis dahin überlieferten mathematischen Aufgaben, Konstruktionen und Überlegungen der Antike. Der Weg des Wissens ging über Ägypten und Babylon ins griechische Kleinasien und von dort erst nach Griechenland. Die Griechen waren die Ersten die durch Anwendung bestimmter Denkstrategien wie Analyse also Deduktion aufs Wesentliche, Axiomenbildung und Beweis, der Mathematik das Werkzeug gaben zu einer Wissenschaft zu werden. Die Wiege der Mathematik aber stand in Ägypten und im Zweistromland. Die Griechen brachten dem Kind lediglich das Laufen bei. Die Konsequenz ist, dass die Beschäftigung der Griechen mit der Quadratur des Kreises ebenfalls ihre Wurzel in Beispielaufgaben, Konstruktionen und Überlegungen aus der Antike gehabt haben muss. Was auf die Existenz von Konstruktionen mit samt den entsprechenden Zahlenverhältnissen und auch Betrachtungen hinweist, die als Vorläufer für die Griechen gedient haben müssen. |
| Hippasos von
Metapont war ein
griechischer Mathematiker und Musiktheoretiker und
gehört zu den bekanntesten Pythagoräern der Frühzeit.
Er lebte im späten 6. und frühen 5. Jahrhundert v. Chr.
Mit seiner Entdeckung der inkommensurabler
Strecken, stellte sich
heraus, dass es konstruierbare Objekte gibt
(beispielsweise die Diagonale eines Quadrates), die nicht
als Verhältnis ganzer Zahlen darstellbar sind. Als Folge dieser Entdeckung trat die Arithmetik zugunsten der Geometrie in den Hintergrund, Gleichungen wurden jetzt geometrisch gelöst, etwa durch Aneinanderlegung von Figuren und/oder durch Überführung verschiedener Figuren in Dreiecke, Rechtecke oder Quadrate. Neben der Dreiteilung dei Winkels, der Verdopplung des Würfels (Delphisches Problem) war die Quadratur des Kreises eines der klassischen Probleme der antiken griechischen Mathematik. Die Aufgabe der Kreisquadratur war, zu einem gegebenen Kreis, nur mit Hilfe von Lineal und Zirkel, ein umfang- bzw. flächengleiches Quadrat zu konstruieren. Eine Beschränkung der Konstruktionsmittel auf Zirkel und Lineal wurde dabei anfänglich nicht generell gefordert. Während der Beschäftigung mit den klassischen Problemen wurden daher auch schon früh Lösungen gefunden, die auf weitergehenden Hilfsmitteln basierten. Es kristallisierte sich im Lauf der Zeit aber eine Haltung heraus, die eine möglichst weitgehende Beschränkung, also auf Zirkel und Lineal, verlangte. Die Konstruktion sollte auch in einer begrenzten Anzahl von Schritten bewältigt werden. Spätestens seit Pappos (um 300 n. Chr.) war diese weitest gehende Beschränkung zur allgemeinen Regel geworden. |
| Anaxagoras (499-428 v. Chr.) war ein Vorsokratiker und
stammt aus Klazomenai in Kleinasien. Er ging um das Jahr
462 v. Chr. nach Athen und machte dort seine Lehren
bekannt und erlebte den politischen Durchbruch zur
entwickelten Attischen Demokratie. Mit Anaxagoras
gelangte die ionische Aufklärung nach Athen. Anaxagoras verbrachte die wichtigsten Jahrzehnte seines Lebens in Athen und stand dem leitenden Staatsmann Perikles als philosophischer Lehrer und Berater nahe. Auch der Tragödiendichter Euripides ließ sich von ihm in das philosophische Denken und Forschen einführen. Um ca. 430 v. Chr. wird Anaxagoras der Gottlosigkeit angeklagt, durch den Einfluss des Perikles zwar vor der Todesstrafe gerettet, aber auf Dauer verbannt. Seine letzten zwei, drei Lebensjahre verbrachte er in Lampsakos im Exil. Sein Werk „Über die Natur“ wurde für eine Drachme in Athen unter der Hand verkauft und beeindruckte auch Sokrates. Dem griechischen Schriftsteller Plutarch (45-125 n. Chr.) zufolge soll Anaxagoras im Gefängnis die Quadratur des Kreises aufgeschrieben oder gezeichnet haben. Nähere Angaben zur Konstruktion von Anaxagoras macht Plutarch jedoch nicht. |
| Hippokrates
von Chios war ein
antiker griechischer Mathematiker und Astronom. Er lebte
um die Mitte oder in der zweiten Hälfte des 5.
Jahrhunderts v. Chr. Hippokrates soll als erster ein Lehrbuch der Mathematik verfasst haben. Es ist verloren; auch sonst ist von seinen Werken nichts erhalten geblieben. Daher können seine Leistungen nur indirekt aus späterer Literatur erschlossen werden. Unter anderem befasste er sich mit dem Problem der Verdoppelung des Würfels („Delisches Problem“), dass er einer Lösung näherbrachte, indem er es in die Planimetrie verlagerte. Über sein Leben liegen keine sicheren Informationen vor. Unzweifelhaft ist seine Herkunft von der Insel Chios. In Anekdoten wird erzählt, dass er auf einer Seereise um sein Vermögen gebracht wurde. Er soll in Athen gelebt haben. Mitunter wird vermutet, er sei von den Pythagoräern beeinflusst gewesen. Nach ihm sind die Möndchen des Hippokrates benannt, bestimmte von Kreisbögen eingeschlossene Flächen, deren Quadratur ihm gelang. Von den Möndchen ausgehend versuchte er die Quadratur des Kreises. Ausgehend von dem bei ihm noch als Axiom benutzten Satz, dass sich die Flächen ähnlicher Kreissegmente wie die Quadrate über ihren Sehnen verhalten, gelang es Hippokrates, von Kreisbögen begrenzte Flächen, die so genannten „Möndchen des Hippokrates“, zu quadrieren.
Da nur bestimmte
Möndchen, z.B. die über der Seite des Quadrates, nicht
jedoch die über der Seite eines regelmäßigen
Sechsecks, quadrierbar sind ist die allgemeine Quadratur
des Kreises auf diese Weise jedoch nicht
zu erreichen. |
| Hippias von
Elis war ein
enzyklopädisch gebildeter Sophist des ausgehenden 5.
Jahrhunderts v. Chr. aus Elis. Er war ein jüngerer
Zeitgenosse des Protagoras, und wurde von Platon in zwei
Dialogen (Hippias Minor und Hippias Maior) sowie im
Dialog Protagoras dargestellt. Hippias war der Erfinder der kinematisch erzeugten Kurve Quadratrix, die zur Lösung von zweien der drei Probleme der griechischen Geometrie, der Drittelung eines Winkels und der Quadratur des Kreises, verwendet wurde.
|
| Antiphon aus Athen war ein griechischer Philosoph
und Sophist des 5. Jahrhunderts v. Chr., der mit einem
Dichter, Tragiker und Traumdeuter identifiziert wird. Der
eine Kunst, kummerfrei zu leben, verfasste und von dem
Cicero Hinweise auf eine Schrift über Traumdeutung
überliefert. Schließlich sind unter Antiphons Namen
auch Überlegungen zur Mathematik überliefert.
Umstritten ist seine Identität mit dem Redner Antiphon. Der Sophist Antiphon verfasste u. a. zwei Schriften über den Gemeinsinn und über die Wahrheit. Aus beiden waren nur kümmerliche Zitate überliefert, bis im 20. Jh. im ägyptischen Oxyrhynchos Papyros-Fragmente mit längeren Abschnitten aus Antiphons Schrift über die Wahrheit gefunden wurden. Da diese für eine Gleichheit aller Menschen (bzw. genauer gesagt Männer) eintreten und sich gegen die Unterscheidung von 'Griechen' und 'Barbaren' aussprechen, kann dies als Argument gegen die Identität mit dem als Oligarchen bekannten Redner Antiphon betrachtet werden. Antiphon war der Meinung, das die Quadratur des Kreises und damit die exakte Bestimmung von π möglich sein müsse. Jedes Dreieck lässt sich in ein Quadrat überführen. Daher lässt sich auch jedes Polygon in ein Quadrat verwandeln. Seine Idee ging davon aus, dem Kreis (regelmäßige) Vielecke mit immer größerer Seitenzahl einzuschreiben, so dass diese schließlich nicht mehr vom Kreis zu unterscheiden sind und damit der Kreis völlig "erschöpft" ist. Auf Grund dieser Vorgehensweise nennt man diese Technik Exhaustions-Methode. Der lateinische Ausdruck heißt "exhaurire", was herausnehmen, erschöpfen, vollenden bedeutet. |
| Bryson von Herakleia (450-390 v. Chr.) war
Mathematiker und Philosoph aus Herakleia Pontike. Er war
ein Schüler des Euklid von Megara. Bryson ging noch einen Schritt weiter als Antiphon und berechnete die Fläche von zwei Vielecken. Eines das den Kreis von innen begrenzte und eines zweiten das den Kreis von außen umschloss. Die Fläche des Kreises, so folgerte Bryson, müsse zwischen den Flächen der beiden Vielecke liegen. Bryson näherte den Kreis durch ein- und umbeschriebene regelmäßige Vielecke an und schloss mit Hilfe des Axioms „Wozu es ein Größeres und ein Kleineres gibt, dazu gibt es auch ein Gleiches“ auf die Existenz eines dem Kreis flächengleichen Vielecks. Damit legten Antiphon und Bryson den Grundstein für die erfolgreiche Arbeit vieler Mathematiker in späterer Zeit, nicht zuletzt des Archimedes, der eben diese Methodik ausbaute und für seine Kreisberechnung benutzte. |
| Eudoxos von
Knidos (zwischen
397 und 390 v. Chr. - 345 und 338 v. Chr.) war ein
berühmter griechischer Mathematiker, Astronom, Geograph,
Arzt, Philosoph und Gesetzgeber der Antike. Seine Werke sind bis auf Fragmente verloren. Daher sind seine wissenschaftlichen Leistungen nur aus Berichten anderer Autoren bekannt bzw. zu erschließen. Mit seiner mathematischen Darstellung der Himmelskörperbewegungen leistete er einen maßgeblichen Beitrag zur Geometrisierung der Astronomie. In der Mathematik begründete er die allgemeine Proportionenlehre. Dabei konnte er erstmals die irrationalen Größen einbeziehen, da seine Proportionenlehre auch auf inkommensurable Größen anwendbar ist. Seine Definitionen von Verhältnis und Proportion sind im fünften Buch von Euklids Elementen überliefert. In der Forschung ist vermutet worden, dass das nach Archimedes benannte Archmedische Axiom in Wirklichkeit von Eudoxos stammt. Die Ausgangsproblematik hat Eudoxos offenbar gekannt, doch inwieweit er sich damit auseinandergesetzt hat, ist unklar. Eudoxos befasste sich mit dem in der Antike intensiv diskutierten Problem der Würfelverdoppelung („Delisches Problem“). Er fand dafür eine nicht näher bekannte Lösung durch den Schnitt von Kurven; deren Schnittpunkte ergaben die zur Lösung des Problems erforderlichen zwei mittleren Proportionalen zur Kante des gegebenen und der des gesuchten Würfels. Ferner erfand Eudoxos, wie Plutarch berichtet, auch eine mechanische Vorrichtung zur annähernden Konstruktion von zwei mittleren Proportionalen. Um 365/364 reiste Eudoxos in Begleitung eines Mitbürgers, des Arztes Chrysippos, nach Ägypten. Ein Empfehlungsschreiben des Königs Agesilaos II. von Sparta ebnete ihm den Weg zum Pharao Nektanebos I. Der Aufenthalt dauerte sechzehn Monate. Sein besonderes Interesse galt den Kenntnissen der ägyptischen Priester, in deren Astronomie er sich Einblick verschaffte. Zu den Schülern des Eudoxos gehörten der Arzt Chrysippos, der ihn nach Ägypten begleitete, die Mathematiker Menaichmos und Deinostratos und der Astronom Polemarchos von Kyzikos. Eudoxos untersuchte die Volumenverhältnisse von Körpern und zeigte, dass das Volumen einer Pyramide einem Drittel des entsprechenden Prismas und dasjenige eines Kegels einem Drittel des entsprechenden Zylinders entspricht. Für seinen Beweis verwendete er ein infinitesimales Berechnungsverfahren, die Exhaustionsmethode. Mit dieser Methode konnte er auch das Verhältnis der Kreisfläche und des Kugelvolumens zum Radius bestimmen. Durch die Idee des Exhaustionsverfahren inspiriert, entwickelte Eudoxos von Knidos die Exhaustionsmethode zu einem funktionierenden Verfahren und berechnete so das Volumen von Pyramide und Kegel. Die Aussage von Antiphon setzt das Wissen bzw. die Idee voraus, dass eine Kreisfläche in ein Quadrat überführt werden kann. Wie beim Papyrus Rhind zu sehen war, setzten die Ägypter die Fläche eines Kreises mit dem Durchmesser 9 einem Quadrat mit der Seitenlänge 8 gleich, d.h. die Idee einen Kreis in ein Quadrat zu transformieren stammt damit von den Ägyptern bzw. letztlich aus dem allgemeinen Fundus der antiken Mathematik. Anaxagoras, Hippokrates von Chios, Hippias von Elis, Deinostratos, Nikomedes und Antiphon greifen auf die Idee der Quadrierung aus der Antike zurück. Dann kann Antiphon, durch das Exhaustionsverfahren, aber als Erster aufzeigen, dass die Quadratur der Kreisfläche eine legitime (weil berechenbare) Konstruktion darstellt. Unter der Vorraussetzung das bei zwei gegebenen Quadraten immer ein Proportionalitätsfaktor existiert, lässt sich auch direkt diese Aussage folgern: Das Quadrat aus dem Durchmesser ist proportional zum Quadrat das die Kreisfläche darstellt. Damit ist das Durchmesserquadrat auch proportional zur Kreisfläche. Dieser Zusammenhang wurde erst 100 Jahre später durch Euklid publiziert, muss aber schon zu Zeiten Antiphons bekannt gewesen sein. |
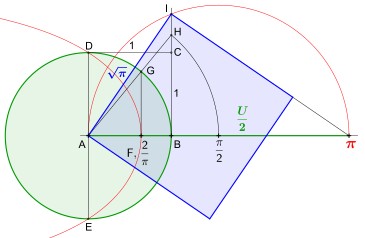
| Deinostratos (ca. 390 v. Chr. bis ca. 320 v. Chr.) war
ein griechischer Mathematiker und Geometer und Bruder von
Menaichmos. Er ist dadurch bekannt, dass er die
Quadratrix des Hippias zur Lösung des Problems der
Quadratur des Kreises entwickelte. Deinostratos’ Hauptbeitrag zur Mathematik war seine Lösung der Quadratur des Kreises. Um dieses Problem zu lösen, nutzte Deinostratos die Trisektrix von Hippias von Elis, die dann später – nachdem Deinostratos das Problem gelöst hatte – als Quadratrix bekannt wurde. Obwohl Deinostratos dieses Problem löste, benutzte er hierfür nicht allein Lineal und Zirkel und daher war es für die Griechen klar, dass seine Lösung gegen die fundamentalen Prinzipien ihrer Mathematik verstoßen hatte. Deinostratos konnte zeigen, dass mit Hilfe der Quadratrix, die Strecke der Länge 2/π (und damit mit Hilfe weiterer elementarer Konstruktionen ein Quadrat der Fläche π) konstruiert werden kann. So gelang ihm die Rektifikation des Viertelkreisbogens und die Quadratur des Kreises. Die Quadratrix selbst ist jedoch eine so genannte transzendente Kurve, also nicht mit Zirkel und Lineal erzeugbar. Daher war die Lösung im strengen klassischen Sinne damit nicht erreicht. |
| Euklid von Alexandria (360-280 v. Chr.) war
Mathematiker. Die überlieferten Werke umfassen
sämtliche Bereiche der antiken griechischen Mathematik:
das sind die theoretischen Disziplinen Arithmetik und
Geometrie, Musiktheorie (Die Teilung des Kanon), eine
methodische Anleitung zur Findung von planimetrischen
Problemlösungen von bestimmten gesicherten
Ausgangspunkten aus (Porismen) sowie die physikalischen
bzw. angewandten Werke (Optik, astronomische Phänomene). In seinem berühmten Werk „Die Elemente“ (vermutlich um 325 v. Chr. entstanden) leitete er die Eigenschaften geometrischer Objekte, der natürlichen Zahlen und bestimmter Größen aus einer Menge von Axiomen (Elementaraussagen) ab. Sein axiomatische Methode wurde zum Vorbild für die gesamte spätere Mathematik. Er trug das mathematische Wissen seiner Zeit zusammen und gibt uns damit einen guten Überblick über den mathematischen Kenntnisstand der Griechen gegen Ende des 4. Jahrhunderts v. Chr. Viele Sätze der Elemente stammen nicht von Euklid selbst. Seine Hauptleistung besteht in der Sammlung und einheitlichen Darstellung mathematischen Wissens. Euklid gelang der Beweis, das 3 < π < 4 gilt. Doch erst Archimedes konnte rund
100 Jahre später diese Ungleichung verfeinern. AKreis ≈ d2 Diese Proportionalität
taucht hier so ganz unvermittelt aus dem Dunkel der
Geschichte auf, muss aber schon länger bekannt gewesen
sein. |
Nikomedes (um 280 v. Chr. bis um 210 v. Chr.) war ein
griechischer Mathematiker, der um die Wende des 3. zum 2.
Jahrhundert vor Christus lebte.
|
| Archimedes von
Syrakus (287-212
v. Chr.) war Mathematiker, Physiker und Ingenieur. Er
gilt als einer der bedeutendsten Mathematiker der Antike,
der u.a. die Gesetze für den Auftrieb, den Hebel und den
Flaschenzug fand. Eine ausführliche Abhandlung von Archimedes mit dem Titel „Kreismessung“ ist dokumentarisch überliefert. Archimedes beweist in seiner Arbeit drei grundlegende Sätze: Satz 1: Die Fläche eines Kreises ist gleich der Fläche eines rechtwinkligen Dreiecks, mit dem Kreisradius als der einen und dem Kreisumfang als der anderen Kathete. Berechnen lässt sich die Kreisfläche dann als AKreis = ½ · Radius · Umfang Archimedes beweist den Satz
indirekt. Indem er die Fläche des Kreises einmal als
größer und einmal als kleiner als die Dreiecksfläche
annimmt. Beide Aussagen werden dann zum Widerspruch
geführt. Die Konsequenz ist daher, dass die Kreisfläche
nur gleich der Dreiecksfläche sein kann. AKreis = d2 · Faktor1 Man kann voraus setzen das eine Rektifikation des Kreises bekannt war, und damit auch diese Beziehung UKreis = d · Faktor2 Bildet man das Produkt Durchmesser mal Umfang dann ergibt sich: d · UKreis = d · (d · Faktor2) = d2 · Faktor2 Also ist das Rechteck aus
Durchmesser (Radius) und Umfang auch proportional zum
Durchmesserquadrat bzw. zur Kreisfläche. Das müsste
schon zu Zeiten Antiphons bekannt gewesen sein. Und ohne
zu wissen das es nur einen einzigen
Proportionalitätsfaktor gibt. AKreis = ½ · Radius · Umfang Durch eine kleine Umstellung der Gleichung entsteht: AKreis = Radius · Umfang/2 Und dies lässt sich unmittelbar
als ein Rechteck interpretieren, mit den Seitenlängen r
und U/2. Dieses Rechteck lässt sich
auch direkt aus der Rektifikationskonstruktion über das 14:11
Dreieck ableiten. Siehe Quadratur
1
Archimedes greift
hier den Gedanken von Bryson auf, nämlich der beliebigen
Annäherung des Kreises durch eingeschriebene und
umschreibende regelmäßige Vielecke. Ausgehend vom
eingeschriebenen Sechseck und einem umschreibenden
Dreieck gelangt Archimedes, durch sukzessive Verdoppelung
der Seitenzahl, jeweils bis zum 96-Eck. AKreis = d2 · 11/14 Der zweite Satz ist eine Folgerung
aus den beiden anderen Sätzen. Das sich die Fläche
eines Kreises proportional zum Quadrat seines
Durchmessers verhält, war ja bereits seit Antiphon
bekannt und erstmals 100 Jahre zuvor von Euklid angegeben
worden. Archimedes gibt hier als Erster explizit den Wert
der Proportionalitätskonstanten mit 11:14 an. AKreis
= ½ · Radius · Umfang = ½ · r · U = ¼ · d · U Zusammen genommen ergibt sich: ¼ · d · U = AKreis = d2 · 11/14 Umstellen der Gleichung zum Umfang hin ergibt: U = d ·
11/14 · 4 = d · 22/7 In einer weiteren Arbeit
„Über Spiralen“ beschreibt Archimedes die
Konstruktion der später nach ihm benannten Spirale, die
durch die Überlagerung einer kreisförmigen mit einer
linearen Bewegung gewonnen wird. |