 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright ©: Klaus Piontzik
| 7.3.0 | Historisches | |
| 7.3.1 | Beispiele aus dem Altertum | |
| 7.3.2 | Weitere Beispiele aus der Architektur | |
| 7.3.3 | Vom Quadrat zum Kreis | |
| 7.3.4 | Beispiele aus der Moderne | |
|
| 7.3.0 | Historisches |
 |
 |
 |
| Die Entwicklung des mathematischen Denkens,
bei getrennt lebenden Völkern, hat sich unter ähnlichen
gesellschaftlichen Bedingungen fast gleich vollzogen. Mit
dem Entstehen der Hochkulturen in Sumer und Ägypten
gegen Ende des 4. vorchristlichen Jahrtausends
entwickelte sich die Mathematik, wohl als religiöses und
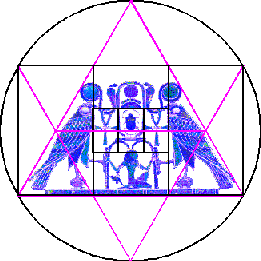
kaufmännisches Instrument. Ein wichtiger Bestandteil der Mathematik waren Maße und Proportionen, da sie in Kunst und Architektur gebraucht wurden. Schon die Arche Noah und der Salomonische Tempel waren, wie die Bibel berichtet, in einfachen aber ganz genau bestimmten Verhältnissen gebaut. Mit ziemlicher Sicherheit darf angenommen werden, dass auch die alten Ägypter ihren Bauten geometrische Maßverhältnisse zugrunde legten. Eingehende Untersuchungen haben ergeben, dass das ägyptische Dreieck, also der bekannte Pyramidenschnitt mit dem Verhältnis von 8 zu 5 zwischen Basis und Höhe "der Schlüssel aller Verhältnisse" in der ägyptischen Baukunst sei. Bei einzelnen Pyramidenbauten scheinen die Maße der Hypotenuse und die halbe Basis nach dem goldenen Schnitt bestimmt zu sein. Und es existieren einige Pyramiden die ein 14:11 Verhältnis aufweisen, wenn man Pyramidenhöhe und Basis betrachtet. Die Griechen haben ihre Tempel nach einer festgesetzten Norm aufgebaut, nach einfachen in ganzen Zahlen ausdrückbaren Verhältnissen. Wobei der goldene Schnitt hier eine besondere Rolle gespielt hat. Wie John Michell in seinem Buch Maßsysteme der Tempel zeigen kann existierten quasi bei allen Völkern, die Hochkulturen hervorbrachten, ganze Systeme von Maßen und Maßverhältnissen also Proportionen und Proportionsmodule. |
| 7.3.1 | Beispiele aus dem Altertum |
|
|
|
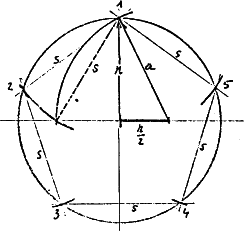
| Die einfachsten Proportionen lassen sich aus den Zahlen 3, 4 und 5 generieren. Durch die Konstruktion entsprechender Polygone. Sowie deren Vielfache wie 6, 8 und 10 oder 12, 16 und 20. |
|
|
|
 |
 |
 |
 |
 |
  |
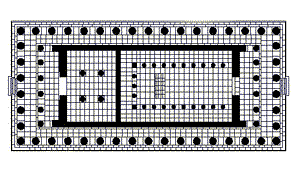| Marcus Vitruvius Pollio Plan einer idealen Stadt |
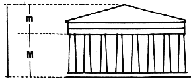
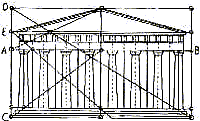
Pharaoh Senwosret | Pantheon Akropolis |
 |
 |
  |
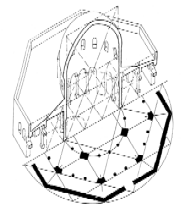
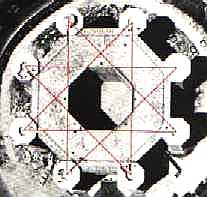
| Felsendom Jerusalem |
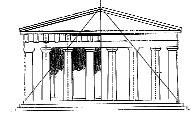
Griechischer Tempel | Griechischer Tempel |
| 7.3.2 | Weitere Beispiele aus der Architektur |
|
|
|
| In der Architektur treten immer wieder Proportionen auf die von den Zahlen 3, 4 und 5 ausgehen. |
 |
 |
 |
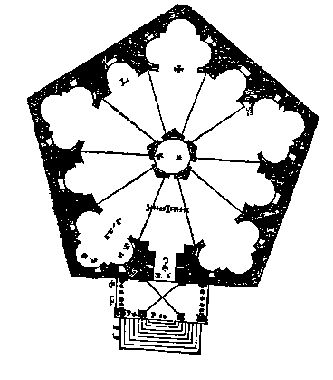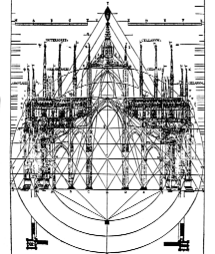
| Castel de Monte | Kathedrale und Dreieck | Kirche von Sebastiano Serlio |
 |
 |
 |
| Tür eines Landhauses | Kathedrale und Dreieck | Haus von Le Corbusier |
| 7.3.3 | Vom Quadrat zum Kreis |
|
|
|
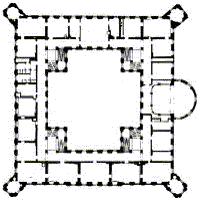
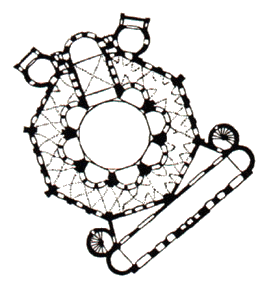
| Es fand eine Entwicklung in der Architektur statt, die vom Quadrat ausgehend über Polygone bis zum Kreis ging. |
 |
 |
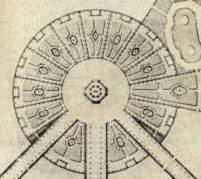| Schloss Tettnang | Tiergarten - Wien |
 |
 |
 |
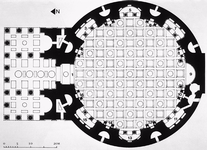| Basilica di San Pietro | Zentralplatz | Pantheon - Rom |
| 7.3.4 | Beispiele aus der Moderne |
|
|
|
| Bis heute werden in der Architektur und Heraldik Proportionen benutzt die auf den Zahlen 3, 4 und 5 basieren. |
 |
 |
 |
| Die heutige Bauweise | Der amerikanische Adler | Das Pentagon USA |
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
