Copyright © Klaus Piontzik
|
Anfangs der 50er Jahre beschrieb Dr. med. Ernst
Hartmann ein energetisches Gittersystem auf der
Erdoberfläche. Ausführliche Experimente dazu sind in
den Büchern „Krankheit als Standortbestimmung“
zu finden. Hartmann sprach von Globalnetzgitter, heute
ist es besser bekannt unter dem Namen Hartmanngitter (Hartmann-Gitter) und
wird in der Radiästhesie, der Baubiologie, der
Geobiologie und auch teilweise in der Architektur
benutzt. Die sogenannten Reizstreifen bzw. –zonen von 20 cm Breite verlaufen in der magnetischen Nord-Süd Richtung in etwa 2m Abstand und in der Ost West Richtung mit etwa 2,5 m Abstand. Ein weiteres Gitternetz, früher auch Diagonalgitter genannt, wurde zwischen 1945 und 1951 von Siegfried Wittmann erstmalig beschrieben. Die eigentlich bekannt gewordene Veröffentlichung stammte 1952 von Dr. Manfred Curry, der den Namen Wittmann allerdings nicht erwähnte. Daher wird es heutzutage meistens einfach Currygitter oder auch Currynetz genannt. Es verläuft von NO nach SW und von NW nach SO. Das Rastermaß beträgt dabei etwa 3,6 m x 3,6 m. Anton Benker entdeckte 1953, dass sich die ganze Erdoberfläche und der darüber liegende Raum in würfelförmige Felder im Abstand von 10 m aufgliedert. Das Benker-Kubensystem wird, in der Regel, als übergeordnetes System zum Hartmann-Gitter gesehen. (siehe dazu auch „Strahlenkunde mit dem Benker-Kuben-System“ von Anton Benker) Es werden allgemein folgende Beziehungen angegeben: In Ost-West Richtung: 1 Benker = 4 Hartmann In Nord-Süd Richtung: 1 Benker = 5 Hartmann |
 |
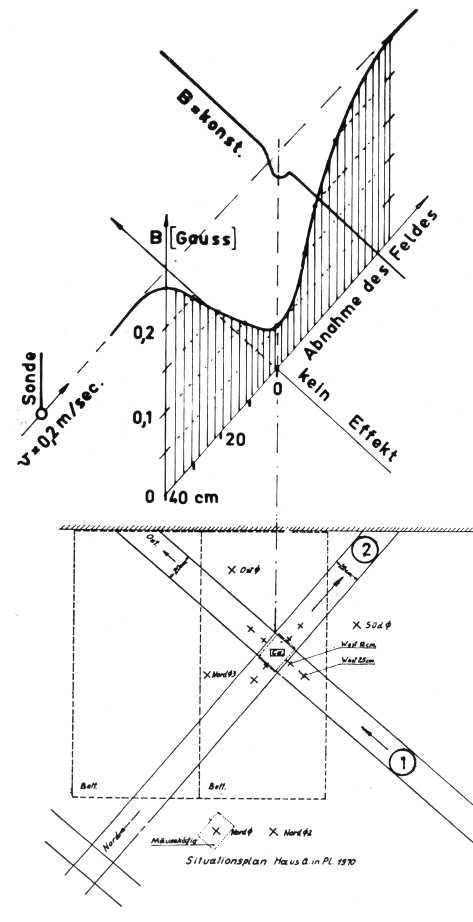Bild 11.1 zeigt einen Versuch, den
Hartmann mit einem magnetischen Sensor (Hallsonde) an
einem Kreuzungspunkt des Gitters ausführte.
Dabei wurde die Sonde einmal in Nord-Süd und dann in Ost-West-Richtung bewegt und dabei die magnetische Flussdichte bestimmt. In Nord-Süd-Richtung ist eine deutlich erkennbare Senke in der magnetischen Flussdichte zu erkennen.In Ost-West-Richtung ist die Abweichung nur minimal. (Siehe dazu sein Buch Krankheit als Standortproblem – Seite 457 (Abb. 263) Mit seinem Hallsonden-Versuch ist Hartmann auf die Schwingungsstruktur des Gitter-Phänomens gestoßen, ohne allerdings die Tragweite zu erkennen. Wenn Hartmann einen Abfall, also eine Senke des magnetischen Feldes, am Orte eines Kreuzungspunktes detektieren konnte, so ist die Konsequenz, dass hier eine Reihe von Senken vorliegt – durch das Gitter bedingt. Zwischen den Senken existieren dann aber auch Höhepunkte. Und eine Folge von Minima und Maxima ist eine Schwingung. |
|
| Abbildung 11.1 - Der Versuch von Hartmann mit einem magnetischen Sensor |
|
Mit seinem Hallsonden-Versuch hat Hartmann den Beweis für den Zusammenhang des
Gitterphänomens mit dem zonalen Anteil des Erdmagnetfeldes erbracht.
Konsequenz: Es existiert ein Zusammenhang zwischen Hartmanngitter und Erdmagnetfeld |
| Aus dem Grundfeldmodell und der Fourieranalyse folgt: der tesserale Anteil des Erdmagnetfeldes besteht aus Grundfeldern bzw. Gittern, d.h. hauptsächlich aus Hartmann-ähnlichen Gitterstrukturen. Die Konsequenz für die bisher aufgeführten Gitter (Hartmann, Curry, Benker) ist: |
Gitter sind
stationäre Schwingungszustände des Erdmagnetfeldes, mit bestimmten
Frequenzen |
 |
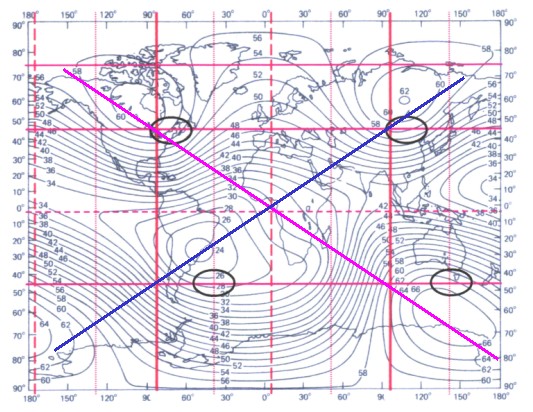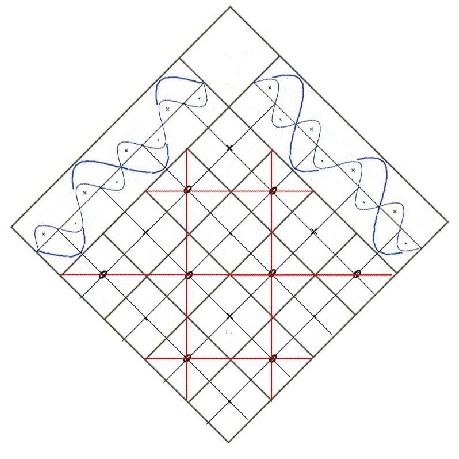
Das Bild zeigt noch mal die ermittelten huygenschen Quellbereiche des tesseralen Feldes (schwarz) mit dem magnetischen Hauptmeridian (rot senkrecht) aus dem sektoriellen Anteil bzw. des Gitters ZS. Siehe dazu Kapitel 9.
Die blaue und die magenta Linie stellen die theoretische (mathematische) Verbindung zwischen idealen Quellpunkten dar, wenn man das Huyhensche Prinzip auf das Erdmagnetfeld anwendet. Das Benker-Kubensystem (Hartmanngitter) ist mit dem erdmagnetischen Schwingungsgefüge (rot) in Nord-Süd-Richtung gekoppelt. Das Currynetz liegt diagonal zum Benkersytem und damit in der Ebene der Quellenverbindungen. |
| Wendet man das Grundfeldmodell auf das Benkersystem (Hartmann-Gitter) und das Currygitter an, so lässt sich folgende Einordnung anwenden: |
|
Das Curry-Netz liegt in der Ebene der Grundschwingungen Das Benkersystem (Hartmanngitter) liegt in der Ebene der Grundfelder |
| Das erlaubt folgenden Ansatz: Das Curry-Netz liegt in der Ebene der Grundschwingungen und das Benkergitter wird durch das Currynetz erzeugt. Der Ansatz erfolgt zunächst in einer euklidischen Ebene. Ort der Betrachtung ist der Schnittpunkt der beiden erzeugenden Schwingungsebenen. |
 |
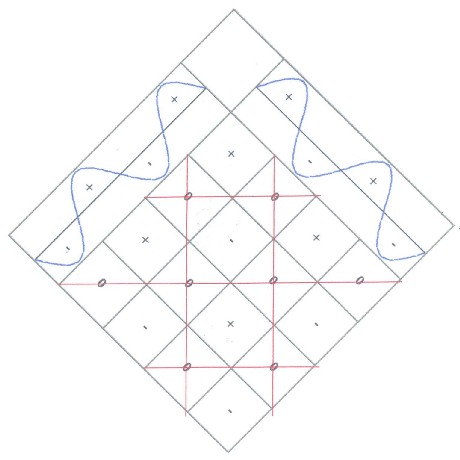Ausgangspunkt ist die Multiplikation zweier Schwingungen nach Kapitel 5.4. Das erzeugte rote Gitter soll dabei das Benkersystem darstellen. Das Benker-Gitter wird durch die (blauen) Grundschwingungen erzeugt. Es gilt: 1 Grundschwingung = 1 Benkerdiagonale |
|
 |
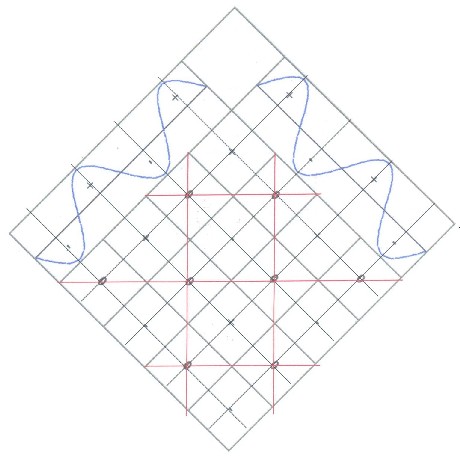Bei idealer Anordnung ergibt sich das Currynetz, wenn das vorhandene Nullgitter halbiert wird. Es gilt dann (lokal eingeschränkt):
1 Benkerdiagonale= 4 Curry | |
 |
Halbierung des Nullgitters bedeutet die doppelte Grundschwingung, also die erste Oberwelle
Das Currynetz ist das Nullgitter der ersten Oberwelle |
Bei idealer Anordnung in einer euklidischen Ebene ergibt sich der Winkel zwischen Currynetz und Benkersystem immer zu 45 Grad.
Es ist noch zu berücksichtigen, dass die gesamte Gittererzeugung auf einer Kugeloberfläche stattfindet. Dort ist der Winkel zwischen Currynetz und Benkersystem nicht konstant, sondern variabel. Insgesamt vom geographischen Standort abhängig. Auf einer Kugeloberfläche existieren daher auch Benker-Kreuzungen die nicht mehr mit den Curry-Kreuzungen zusammen fallen.
| |
|
|
Das Curry-Netz ist das erzeugende Schwingungssystem Das Curry-Netz ist das Nullgitter der ersten Oberwelle der Grundschwingung Das Benker-Gitter wird durch die Grundschwingung erzeugt 1 Grundschwingung = 1 Benkerdiagonale = 4 Curry |
| Wie bereits in Kapitel 7.2 erwähnt, fanden zwischen
1978 und 1979 in Pfaffenhofen an der Ilm Messungen statt,
die zur Entdeckung der Sferics führten. Die
Grundfrequenz der Sferics wird mit f = 4150,84 Hertz
angegeben.
Dieser Wert lässt sich benutzen, um eine Rückberechnung für den Erdradius zu machen. Die Gleichung für die Grundfrequenzen der Erde lautet: |
 |
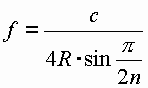| Umstellen nach R ergibt: |
 |
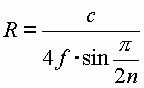| Für n=1 lautet die allgemeine Gleichung für den Erdradius: |
 |
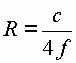| Zu berücksichtigen ist noch das die Sfericfrequenz von 4150,84 Hz das 11·25 = 352fache der Grundfrequenz beträgt. |
| Die Erdgrundfrequenz f0 ergibt sich damit zu 11,79215909 Hz |
|
Mit c = 299792458 m/s als
Lichtgeschwindigkeit ergibt sich für den Radius: R=6355758,426 m = Lo
Dieser Radius Lo heisst von nun an: Grundhüllenradius |
| Damit lässt sich das Schwingungsgefüge für die Erde definieren: |
| Erd-Schwingungsgefüge = Summe aller möglichen Raumgitter auf der Grundhülle |
|
Gebildet werden nun die Differenzen zwischen den
Daten aus einem Geodätischen Referenzsystem und dem
errechneten Radius, also der Grundhülle. Die Daten des Geodätischen Referenzsystems WGS84 sind: Polradius : 6356752 m |
|
Bildet man nun die Differenzen ergibt sich folgende
Situation: Polradius - Grundhüllenradius = 993 m (etwa 1 km) Äquatorradius - Grundhüllenradius = 22378 m (etwa 20 km) |
| Die
Grundhülle auf der die Nulllinien und Extrema liegen, befindet sich zwischen einem und zwanzig Kilometer unter der Erdoberfläche |
| Und damit ist ein Ansatz gegeben, die Streifenbildung innerhalb der Gitter zu erklären. Durch den stationären Zustand bedingt, entstehen außer Maximal- und Minimalfronten auch Nullfronten, die sich kugelförmig um die Quellpunkte, in regelmäßigen Abständen ausbilden. Da der Grundhüllenradius kleiner als die Erdoberfläche ist, entstehen an der Oberfläche keine Linien sondern Streifen. Die folgende Abbildung 11.2. veranschaulicht die daraus abzuleitende Entstehung von Streifen auf der Erdoberfläche. |
 |
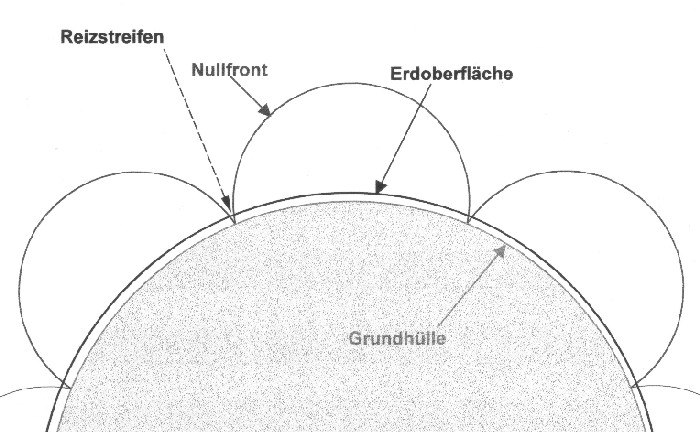| Abbildung 11.2 - Die Streifenbildung durch die Grundschwingungen |
| Demnach bilden die Reizstreifen Gebiete verminderter Intensität, also keine eigentlichen Nullzonen. Als Konsequenz ergibt sich, dass ein Teil der Reizstreifen, global gesehen, in ihrer Breite nicht konstant sind. Die Streifen, die quasi die Meridiane des Schwingungssystems bilden, haben am „Äquator“ ihre größte Breite und werden zu den „Polen“ hin immer schmaler. Lediglich die Streifen die die Breitenkreise des Schwingungssystems bilden, verfügen über eine konstante Breite. |
| Gleichzeitig ergibt sich durch die radialen Komponenten der Grundfelder ein Ansatz, der das Benker-Kubensystem erklären kann. In der Abbildung 11.3 ist die Schwingungssituation im Querschnitt und für eine Frequenz dargestellt. Von den Quellpunkten P ausgehend, bilden sich, nach dem Huygenschen Prinzip, um jeden Quellpunkt konzentrische Kreise von Minimal (rote Kreise)- bzw. Maximalzonen (blaue Kreise) aus. Da ein stationärer Zustand besteht, sind die Wellenfronten in der räumlichen Lage feststehend. |
 |
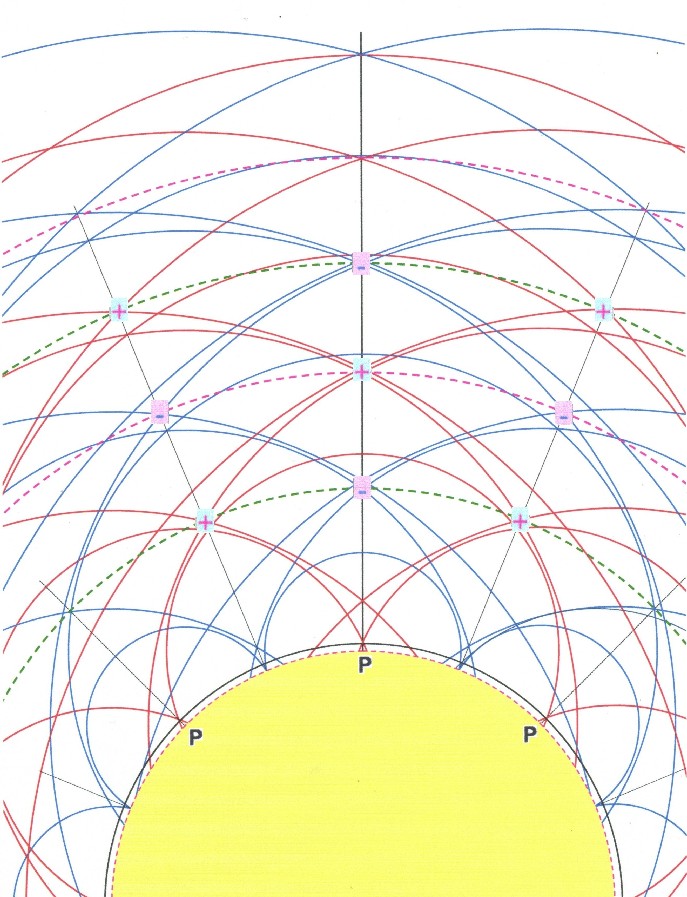| Abbildung 11.3 - Interferenzen der Grundschwingungen |
| Durch die Interferenz also Überlagerung
verschiedener Wellenfronten entstehen Schwingungsmaxima
(mit plus gekennzeichnet) und Minima (mit minus
gekennzeichnet) – zwar da, wo mehrere Wellenfronten
einen Schnittpunkt bzw. ein Ballungszentrum bilden. Die so entstandenen Schwingungsextrema liegen wiederum auf Kugeloberflächen (gestrichelt gezeichnete Kreise) die die Erde konzentrisch einhüllen. Bemerkenswert ist, dass sich eine symmetrische Konfiguration ausbildet. Es entsteht ein räumliches Gittergefüge von Extremalpunkten, das den Raum um die Erde vollständig erfüllt. Alle Plus- und Minusbereiche folgen abwechselnd aufeinander. |
| Auf den entstandenen kugelförmigen Hüllen bilden sich Maxima und Minima aus. Und wie bei den Grundfeldern (siehe Kapitel 5.5) entstehen dazu die zugehörigen Nulllinien bzw. Nullfronten. |
 |
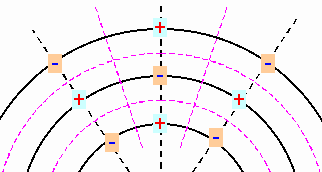Die einzelnen Hüllen (Grundfelder) sind
zueinander um 180 Grad phasenversetzt. - Und aus diesem
Grunde können zwischen den Extrema nun, sowohl in
senkrechter (radialer) als auch in tangentialer Richtung,
ganze Nullflächen (magenta) entstehen. |
|
| Abbildung 11.4 - Räumliche radiale Gitterschwingungen |
| Diese Nullflächen bilden die Wände eines gitterförmigen Schwingungssystems, wobei die Extrema sich punktförmig im Mittelpunkt des jeweils einhüllenden Quaders befinden. Wie in der Abbildung 11.4 ebenfalls zu sehen, ist die Bezeichnung Kuben-System nicht ganz korrekt. |
| Das Benker
Kubensystem ist ein räumliches radiales
Schwingungssystem mit einer Gitterstruktur |
| Boden- und Deckenflächen sind dabei gekrümmt –
es handelt sich ja um Teile der kugelförmigen
Potentialhüllen. Und die Seitenwände sind, wegen der
radialen Ausrichtung, auch nicht parallel zueinander. Das
Ganze kann also nur in einer ersten Näherung
als Kubensystem bezeichnet werden. In der Folge sind alle magnetischen Oberflächenfelder als Teile des gesamten räumlichen Schwingungssystems zu verstehen, da sie als jeweilige Schwingungsschicht im Ganzen enthalten sind. |
| Insgesamt zeigt sich, das die Grundfelder (Hartmann-Gitter) und das radiale gitterförmige Schwingungssystem (Benker-Kuben-System) nicht nur zwei verschiedene Erscheinungsweisen desselben Phänomens darstellen, sondern sich gegenseitig sogar bedingen |
11.4 - Globalnetzgitter (GNG) |
| Durch die Interferenz von magnetischen Wellen bestimmter Frequenzen entstehen Schwingungsschichten die entsprechende Gittersysteme als stationäre Zustände ausbilden. D.h. aber auch, das sich hier mehrere Gittersysteme aufbauen können, die sich lediglich durch ihre Frequenzen bzw. ihre Teilungsverhältnisse unterscheiden. |
| Globalnetzgitter sind stationäre
räumliche Schwingungszustände des Erdmagnetfeldes Globalnetzgitter sind mit bestimmter Frequenzen verbunden |
| Da alle diese Gitter auf ganzzahligen
endlichen Zahlen beruhen, kommt es hier auch zu etlichen
Teilungsverhältnissen. In der Praxis bedeutet dies, dass sich mehrere Gitter, in gleichmäßigen Abständen, in den Reizstreifen (Nullzonen) überlappen können. |
|
| Damit deckt sich das bisher abgeleitete Modell mit den in der Radiästhesie gemachten Aussagen über Globalnetzgitter | |
| Hier muss noch einmal darauf hingewiesen
werden, dass sich ein komplettes, streckenmassig
quadratisches, Gitter auf einer Kugel nicht verwirklichen
lässt. Real entstehen Schwingungssysteme, die gestaltet
sind wie das geographische Gittersystem. Es existieren
immer zwei Pole (die nicht unbedingt identisch sind mit
den geographischen Polen) und die jeweils zugehörigen
„Meridiane“ und „Breitenkreise“
bilden ein Gittersystem. Daraus folgt auch, dass die Gitterquadrate nur am „Äquator“ des Schwingungssystems wirklich quadratisch sind. Zu den Polen hin werden es immer mehr Rechtecke bzw. Rauten und an den Polen selbst findet man schließlich Dreiecke vor. |
|
Das Verlagern von Reizstreifen |
|
| (Ergänzung zur Fachtagung für Geobiologie 29.06.-01.07.2007 in Waldbrunn) | |
| In der radiästhetischen Praxis
sind eine Reihe von Beobachtungen gemacht worden, die das
Phänomen einer lokalen
bzw. regionalen dauerhaften Verlagerung von Reizstreifen
betreffen. Das Gittermodell sagt dazu folgendes: |
|
|
Unterirdische Objekte (Bodenschätze, Verwerfungen, Magmablasen) können lokal wie regional zu einer Verlagerung der Reizstreifen führen. Jedes größere Objekt hat kapazitive (Kunststoffe, Erden) und/oder induktive (Metalle) Eigenschaften. Dies kann zu einer lokalen bzw. regionalen Verzerrung der Gitter führen. |
| In der radiästhetischen Praxis
sind eine Reihe von Beobachtungen gemacht worden, die das
Phänomen einer temporären
Verlagerung von Reizstreifen
betreffen. Das Gittermodell lässt hier folgende Erklärung zu: |
|
| Das räumlich radiale Gittersystem
entsteht als Interferenz bzw. als Summe aller
Grundschwingungen – ist also ein Schwingungssystem. Oder physikalisch ausgedrückt: das gesamte magnetische Gittersystem ist ein harmonischer Oszillator. Genau genommen sogar ein gedämpfter harmonischer Oszillator. Dabei sind die Gitterwände nicht als starr zu betrachten, sondern durch die Schwingungsgrundlage eher als energetische Schwingungszustände zu sehen. Und damit sind sie auch in gewissen engen Grenzen variabel. Die Konsequenz ist: das Gittersystem kann in sich kleine Schwingungen hervorbringen, die sich dann in einer Lageveränderung der Reizstreifen äußern. Die Reizstreifen schwingen dabei also hin und her. Das gilt in nord-südlicher Richtung als auch in ost-westlicher Richtung. Normalerweise müssten diese Schwingungen aber so klein sein, dass sie vernachlässigbar sind. Weiterhin ist auch eine leichte Pulsation des gesamten Systems denkbar und damit ist eine leichte Pulsation (in der Breite) der Reizstreifen gegeben. |
|
| Nun gibt es aber drei Fälle bei denen temporär erkennbar größere Abweichungen der Reizstreifen auftreten müssten. | |
| Im ersten Fall kann durch, geologische Prozesse bedingt, eine Deformation der Reizstreifen vorkommen. Da die geologischen Schalen mit magnetischen Schichten verbunden sind (siehe Kapitel 13), können lokale geologische Effekte, wie eine kleine Verschiebung von tektonischen Platten bzw. Plattenanteilen, (elektro)magnetische Entsprechungen besitzen. Und diese elektromagnetischen Ereignisse können, solange der geologische Vorgang dauert, das Gittersystem lokal kurzfristig verzerren oder auch zum Schwingen bringen. | |
| Im zweiten Fall kann durch, solare Einflüsse, ein globales Schwingen der Reizstreifen auftreten. Da auch die atmosphärischen Schichten mit magnetischen Schichten verbunden sind (siehe Kapitel 14) können z.B. Sonnenstürme, wenn sie auf die Magnetosphäre auftreffen, das gesamte Gittersystem ins Schwingen bringen bzw. zu einer temporären Verlagerung der Reizstreifen führen. | |
| Im dritten Fall kann durch das Ausfallen der solaren Einsolare Einflüsse z.B. bei Sonnenfinsternissen eine kurzzeitige Verlagerung der Reizstreifen auftreten. | |
| In allen drei Fällen können durchaus Schwingungsweiten von einem Meter auftreten. | |
| Nun gilt es noch folgendes zu
berücksichtigen: Die eigentlichen erdmagnetfelderzeugenden Elemente sind magmatische Ströme in etwa 2900 Km Tiefe. Diese Ströme sind zu träge und auch zu stark um von kurzfristigen geologischen oder solaren Ereignissen beeinträchtigt zu werden. Daher hat auch das magnetische Erdfeld und damit auch das magnetische Gittersystem ein gewisses Beharrungsvermögen. Und dieses Verharrungsvermögen wirkt allen äußeren Einflüssen entgegen. Daher kann man das magnetische Gittersystem auch als gedämpften harmonischen Oszillator verstehen. |
|
| Dabei verhält sich das System wie im sogenannten „aperiodischen Grenzfall“. Die Eigenfrequenz und der Reibungsanteil des Oszillators halten sich hierbei gerade die Waage. Daher kommt es bei einer äußeren Einwirkung auf den Oszillator zu einer einmaligen Reaktion, in Form eines Ausschlages. Danach kehrt das System dann langsam wieder in seinen Ruhezustand zurück. | |
| Mit den Längenangaben für das Hartmann-Gitter bzw.
das Benker-Kubensystem und dem Grundfeldmodell lässt
sich eine überschlägige Rechnung
tätigen, mit der die zugehörigen Gitterfrequenzen
ermittelt werden können. Das Hartmann-Gitter hat in der Ost-West-Richtung etwa 2,5 Meter Ausdehnung. Je vier Hartmann-Felder passen in einen Benker-Kubus, so dass sich die Länge eines Kubus zu 10 Meter ergibt. Laut Grundfeldmodell (Kapitel 5) sind aber zwei Kuben (ein positiver und ein negativer) erforderlich um eine Schwingung zu generieren. Für eine Wellenlänge ergibt sich also 20 Meter. Zu berücksichtigen ist noch, dass die benutzten Längen auf den nordeuropäischen bzw. deutschen Raum bezogen sind. Im Mittel wurde hier der 51te Breitengrad angenommen. Zur Umrechnung auf Äquatorebene muss die gegebene Strecke durch den Kosinus der geographischen Breite geteilt werden. So ergibt sich für die Wellenlänge eine Größe von 31,78 Meter am Äquator. Im Übrigen passen so 2513189 Kuben um die Erde herum, bezogen auf den Grundhüllenradius. Der allgemeine Zusammenhang zwischen Wellenlänge und Frequenz ist definiert mit: f·λ = c. Mit λ = 31,78 m erhält man als zugehörige Frequenz: |
| f = 9433368,722 Hz. |
| Untersucht man die gefundene Frequenz mit der Erdfrequenz fo=11,79215909 Hz aus Kapitel 11.2 hinsichtlich der Teilungsverhältnisse, so findet sich ein verblüffend einfache Primfaktorenzerlegung: |
| 11,792 · 28 · 55 = 11,792 · 800000 = 9433600 |
| Allgemein lässt sich daraus ableiten, dass das
Benker-Kubensystem in einem Frequenzbereich von 9,433 -
9,434 MHz schwingt. Das Hartmann-Gitter hat die vierfache
Frequenz, also 37,732 - 37,736 MHz in Ost-West-Richtung. In Nord-Süd-Richtung passen fünf Hartmann-Felder in einen Benker-Kubus. Daher tritt beim Hartmann-Gitter noch der Frequenzbereich 47,165 - 47,17 MHz auf. Daraus ergibt sich: |
| Hartmann-Gitter und Benker-Kubensystem stehen in Relation zur Erdfrequenz |
| Wendet man das Grundfeldmodell aus Kapitel 5 auf das
Hartmann-Gitter und das Curry-Netz an, dann gehört das
Hartmann-Gitter zu den Grundfeldern. Nach dem Modell
liegen die Grundschwingungen diagonal zum erzeugten
Gittersystem. Somit liegt das Curry-Netz in der Ebene der
Grundschwingungen. Betrachtet man nun ein Hartmannfeld mit den beiden Curry-Diagonalen so lassen sich - durch Verlängerung der Diagonalen - auf einer Kugel zwei Kreise konstruieren, die senkrecht auf einander stehen. Siehe dazu Abbildung 11.5. Nun kann aber, geometrisch wie physikalisch, jeder dieser beiden Kreise als Grundmeridian eines Schwingungssystems genommen werden. Und daraus er-geben sich zwei Schwingungssysteme. Was für das eine System der Hauptmeridian ist für das andere System der Äquator. Wobei die beiden Systeme in Frequenz und Phase harmonieren müssen. |
|
| Abbildung 11.5 - Zwei Schwingungsysteme mit vier Polen |
| Es bilden sich so insgesamt vier Pole.
Es entstehen auf der Nordhalbkugel die beiden Pole P11
und P21. Auf der Südhalbkugel entstehen die
zugehörigen Gegenpole P12 und P22.
Aus Symmetriegründen liegen alle Pole dann auf ± 45
Grad geographischer Breite. Schaut man sich das Gesamtfeld aus Kapitel 2 dazu an, so sind da ja tatsächlich vier extremale Bereiche: das Nordmaximum, die große Anomalie, das Südmaximum und das Minimum. Die Existenz der großen Anomalie neben dem Nordmaximum bestätigt hier die Existenz zweier Schwingungssysteme. Die Konsequenz ist: |
| Es
existieren zwei Grundschwingungssysteme (Curry-Netze) Die beiden Schwingungssysteme überlappen sich gegenseitig, da sie senkrecht aufeinander stehen |
| Einen weiteren Hinweis liefert hier der magnetische Rücken in der Arktis, der durch Addition des zonalem mit dem sektoriellen Anteil des Erdfeldes entsteht. Der magnetische Rücken stellt ja die Maximalzone des Grundfeld ZS dar. (vergleiche Kapitel 9.7) Und er ist auch die direkte Verbindung zwischen den beiden nördlichen Polen. Verlängert man diese Verbindung, ergibt sich der schwarze Vollkreis aus Abbildung 11.5. Diesen Kreis haben beide Schwingungssysteme gemeinsam. Daher bildet sich hier quasi ein Hauptmeridian des Gesamtsystems aus. Und genau das ist die Maximalzone des Grundfeld ZS. Der Hauptmeridian liegt bei λ = -83,5 Grad West und λ = 96,5 Grad Ost und ist mit der Maximalzone des Gitter ZS (bzw. des sektoriellen Feldanteiles) identisch. |
| Die Existenz eines magnetischen Minimums lässt sogar noch einen weiteren Schluss zu: Über der Achse Nordmaximum - Südmaximum (P11 und P12) hat sich ein System mit geraden Schwingungen aufgebaut. Das bedeutet, dass sich an beiden Polen Schwingungsmaxima bilden. Über der Achse Große Anomalie - Minimum (P21 und P22) hat sich ein System aus ungeraden Schwingungen aufgebaut. Daraus folgt, dass sich an einem Pol ein Schwingungsmaximum aufbaut und am entgegengesetzten Ende ein Minimum herrscht. Durch die Summenbildung der beiden Systeme entstehen so dann drei Maxima und ein Minimum. |
| Bezüglich der Schwingungsstruktur gibt es nur drei Möglichkeiten. Im ersten Fall existieren zwei gerade Grundschwingungen - dann entstehen vier Maxima. Im zweiten Fall kommt eine ungerade und eine gerade Schwingung vor – dann entstehen 3 Maxima und ein Minimum. Im dritten Fall existieren zwei ungerade Grundschwingungen – dann entstehen zwei Maxima und zwei Minima. |
| In Kapitel 10.2 konnte gezeigt werden, dass quasi
alle magnetischen Extremwerte - geographisch
längenmässig gesehen - in schmale Bereiche hinein
passen. Praktisch alle Extremwerte auf der Nordhalbkugel
lassen sich in einer Zo-ne von 55-90 West bzw. 90-125 Ost
unterbringen. Die Extremwerte auf der Südhalbkugel
lassen sich in einer Zone von 25-50 West bzw. 130-155 Ost
einordnen. Dabei ist der Bereich auf der Nordhalbkugel
unterschiedlich zur Südhalbkugel. Die Extremalzone auf
der Nordhalbkugel ist um etwa 35-40 Grad gegenüber der
südlichen Extremalzone verschoben. Das lässt den Schluss zu, dass die beiden Polachsen der Schwingungssysteme real nicht in einer Ebene liegen, wie in Abbildung 11.5 dargestellt, sondern gegeneinander verschoben sind. Damit verlaufen die Polachsen auch nicht durch den Mittelpunkt der Erde. Da angenommen werden kann, dass die vier Pole in den im Kapitel 10.2 vorgestellten Extremwertbereichen mit enthalten sind, lassen sich jetzt die Koordinaten für die Bereiche, in denen sich die Quellpunkte des Erdfeldes befinden, bilden: |
Quellpunktbereiche für Schwingungssystem 1
| Name | Breite | Länge |
| Nord-Maximum | +45° Nord | -55° bis 90° West |
| Süd-Maximum | -45° Süd | +130° bis 155° Ost |
Quellpunktbereiche für Schwingungssystem 2
| Name | Breite | Länge |
| Grosse Anomalie | +45° Nord | +90 bis 125° Ost |
| Minimum | -45° Süd | -25° bis 50° West |
| Durch Mittelwertbildung der Längenbereiche sind so näherungsweise die Koordinaten der Quellpunkte bestimmbar: |
Koordinaten der Quellpunkte für Schwingungssystem 1
| Name | Breite | Länge |
| Nord-Maximum | +45° Nord | - 72,5° West |
| Süd-Maximum | -45° Süd | + 142,5° Ost |
Koordinaten der Quellpunkte für Schwingungssystem 2
| Name | Breite | Länge |
| Grosse Anomalie | +45° Nord | + 107,5° Ost |
| Minimum | -45° Süd | - 37,5° West |
| Das Grundfeldmodell und das Huygensche Prinzip (Kapitel 5) vorausgesetzt, stellen diese vier Pole die theoretischen Quellpunkte dar, von denen aus sich das gesamte äußere magnetische Feld der Erde aufspannen lässt. |
| Trägt man nun alle gefundenen magnetischen Extrema und Punkte in eine Gesamtkarte der Totalintensität ein, so ergibt sich Abbildung 11.6.: |
 |
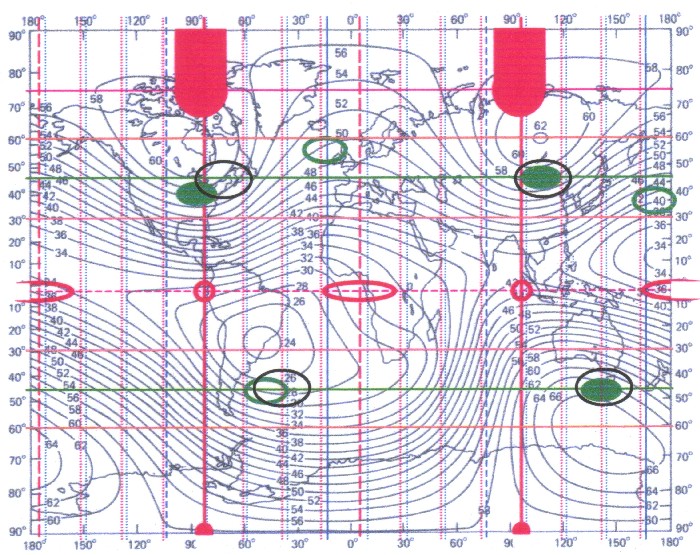| Abbildung 11.6 - alle gefundenen magnetischen Extrema und Punkte |
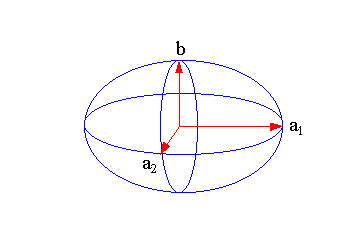
| Die blauen Linien stellen die Achsen eines dreiachsigen Ellipsoid, mit einer 45 Grad-Teilung dar. Das Grundfels ZS ist rot dargestellt. Alles Grüne beschreibt das tesserale Feld. Und die schwarzen Markierungen beinhalten die Quellpunktbereiche. |
| Auffallend
ist die Übereinstimmung der Quellpunktbereiche mit den vier Hauptextrema des tesseralen Feldes |
| Die tesseralen Extremas entstammen der Fourieranalyse aus Kapitel 8 bis 10, während die Quellpunktbereiche durch eine Auswertung der geographischen Länge aller magnetischen Extrema in Kapitel 10 gewonnen wurden. Da das tesserale Feld aus Gittern besteht, sind die Quellpunkte (als Summe) in den Gitterstrukturen also mit enthalten bzw. spiegeln sich darin wieder. |
| Gut zu erkennen ist auch der Hauptmeridian des
Gesamtsystems, also die Maximalzone des Grundfeld ZS bzw.
des sektoriellen Feldanteils bei λ = -83,5 Grad West
und λ = 96,5 Grad Ost. Auf der Nordhalbkugel befinden sich Hauptmeridian (und damit auch das Grundfeld ZS) in Phase mit den tesseralen Extremwerten und den Quellpunktbereichen. Auf der Südhalbkugel sind die tesseralen Extremwerte bzw. die Quellpunktbereiche um etwa 20 Grad gegenüber dem Hauptmeridian verschoben. Was einen Hinweis darauf liefert, dass es in der inneren Erdstruktur einen „Störfaktor“ gibt, der den Aufbau eines mathematisch reinen Feldes verzerrt. Trägt man nun alle gefundenen magnetischen Extremlinien mit den Quellpunktbereichen in eine Gesamtkarte der Totalintensität ein, so ergibt sich Abbildung 11.7. bzw. das B-Gitter der Erde: |
 |
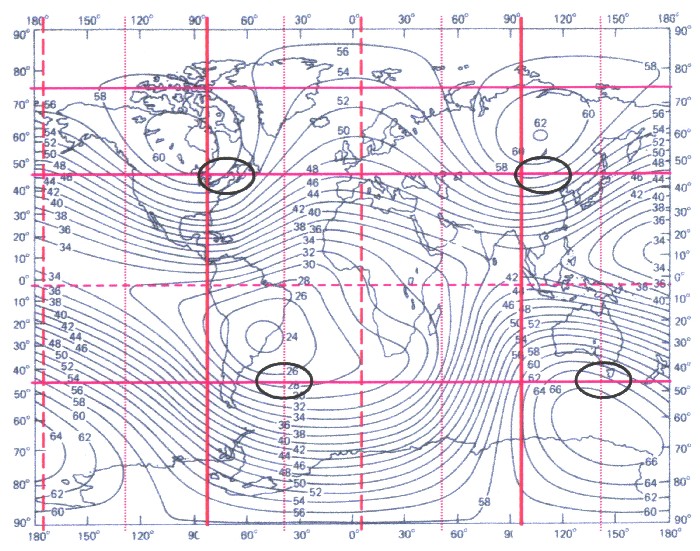| Abbildung 11.7 - Das B-Gitter mit den Quellpunktbereichen |
| Das B-Gitter enthält alle Informationen aller auftretender Teile des Erdfeldes. Gut zu erkennen ist, dass alle Quellpunktbereiche in Phase zum Hauptmeridian bei 83,5 Grad West liegen. Das bedeutet, dass der Störfaktor im Inneren der Erde zwar das Erdfeld verschiebt, dies aber in Harmonie zum Gesamtfeld geschieht. |
| Es existieren zwei Möglichkeiten, den Quellpunktbereichen einem Körper im Erdinneren zuzuordnen: Entweder ein um etwa 35-40 Grad verdrehtes Spat bei dem nur die Hälfte der Ecken besetzt ist, oder ein um etwa 35-40 Grad verdrehtes Tetraeder. |
| Die einzelnen Teile aus der Fourieranalyse und alle gefundenen magnetischen Extrema und Punkte erlauben eine stereometrische Analyse und Darstellung der Gesamtsituation. |
|
In die Karte der Totalintensität werden alle Extremwerte, magnetischen Strukturen und Quellpunkte eingetragen, die sich durch die Analyse ergeben. Blau – dreiachsiges Ellipsoid Rot – Zonal, Sektoriell (Gitter ZS) Grün – Tesseral Schwarz – Quellpunkte |
 |
Das rote magnetische System stellt das Gitter ZS, also den zonal-sektoriellen Teil dar. Sichtbar wird, dass ein magnetischer Rücken am Nordpol entsteht, während am Südpol nur eine punktförmige Maximalzone vorhanden ist. Die Maximumzone = magnetischer Hauptmeridian (dick rot) ist gut zu erkennen, und zwar bei λ = -83,5 Grad West und λ = 96,5 Grad Ost. Die Minimumzonen (rot gestrichelt) liegen bei λ = 5,25 Grad Ost und bei λ = -174,25 Grad West. In der äquatorebene befinden sich zwei Minimalzonen und zwei Sattelpunkte. Alle Extremwertzonen liegen auf den Ecken eines Oktaeders |
|
 |
Das grüne System stellt den tesseralen Anteil dar. Alle Extremwerte liegen etwa bei ±45 Grad Breite. Die grünen Punkte stellen die Maximal- bzw. Minimalpunkte des reinen Gitteranteils des Erdmagnetfeldes dar. Vollgrün = Maximum, Grün Umrandet = Minimum Auf der Nordhalbkugel liegen alle Extremwerte annähernd auf einem Quadrat. Durch die 45 Grad Breite wird koordinatenmäßig in der Erde ein verdrehter Spat (Kubus) aufgespannt. Die Extremalzonen auf der Südhalbkugel sind um etwa 35-40 Grad gegenüber den nördlichen Extremalzonen verschoben. |
|
 |
Die Schwarz umrandeten Ellipsen stellen die Quellpunkte des Gesamtfeldes dar. Das Grundfeld- bzw. Gittermodell und das Huygensche Prinzip vorausgesetzt, stellen diese vier Pole die theoretischen Quellpunkte dar, von denen aus sich das gesamte äußere magnetische Feld an der Erdoberfläche aufspannen lässt. Übereinstimmung der Quellpunktbereiche mit den vier Hauptextrema des tesseralen Feldes. Die Quellpunkte liegen auf den Ecken eines Tetraeders. Die Quellen auf der Südhalbkugel sind um 45 Grad verschoben |
|
 |
Mit Hilfe der Satellitengeodäsie sind 1966 durch C.A. Lundquist und G. Veis folgende Parameter ermittelt worden um die Erde als echtes dreiachsiges Ellipsoid darzustellen: a1-a2 = 69 Meter und λ0 = -14,75 Grad West Das blaue Ellipsoidgitter orientiert nach dem Wert von Lundquist und Veis ist zum roten magnetischen System um 1,25 Grad verschoben. Global gesehen ist also eine gute Übereinstimmung festzustellen.Das Erdmagnetfeld steht in Relation zur Erdgestalt |
|
Eine Analyse der geographischen Positionen aller auftretenden magnetischen Extrema ergibt einen funktionalen Zusammenhang für deren geographische Länge:
λE = 3,75° · m – 13,5° 3,75° durch eine 96er Teilung, m ist Element der ganzen Zahlen Durch die 96er-Teilung ist eine ausreichende Differenzierung vorhanden, um alle auftretenden Winkel für Polyeder bzw. die platonischen Körper zu enthalten. Konsequenz: |
| Alle Platonischen Körper sind als Schwingungsfiguren möglich |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
