 |
|
| 10.0 | Die Schmiegekreis-Konstruktion |
 |
 |
 |
| Die Schmiegekreise spielen bei der Ellipse eine besondere Rolle. Einerseits kann mit ihnen die Ellipse relativ schnell konstruiert werden. Andererseits werden die Radien der Schmiegekreise, speziell der kleinere Radius, benutzt, um die Ellipse in ihren Eigenschaften zu beschreiben, z.B. für die Ellipse als Kegelschnitt. |
| Hier die Konstruktion der Schmiegekreise: |
 |
| Abbildung 10.1 - Konstruktion der Schmiegekreise |
|
| 10.1 | Schnittpunkt Diagonale AB mit der Schmiegekreisgeraden |
|
|
|
| Bei
dieser Konstruktion fällt auf der Schmiegekreisgeraden
noch ein weiterer Schnittpunkt an. Nämlich der
Schnittpunkt der Gerade mit der Diagonalen. Dieser Punkt
wird hier mit SG bezeichnet. Schmiegekreisgerade und Diagonale stehen ausserdem senkrecht aufeinander. Das ist in der folgenden Abbildung noch einmal vergrössert zu sehen |
 |
| Abbildung 10.2 - Schnittpunkt zwischen Schmiegekreisgerade und Diagonale |
| Die Koordinaten des Schnittpunktes SG lassen sich rein analytisch, also mathematisch, ermitteln. Die Ableitung für den Schnittpunkt geschieht folgendermassen: |
| Die Funktionsgleichung für die Schmiegekreisgerade: |  |
| Die Funktionsgleichung für die Diagonale: |  |
| Für den Schnittpunkt SG gilt dann : yS = yD |
| Durch Einsetzen der Geradengleichungen und Auflösen nach x erhält man die x-Komponente für den Schnittpunkt. |
 |
| Durch Einsetzen des gefundenen x in eine der Geradengleichungen erhält man dann die y-Komponente. |
 |
| 10.2 | Der Schnittpunkt mit der Ellipse |
|
|
|
| Auffallend ist, das die y-Koordinate, also die Parallele zur x-Achse, die Ellipse im Punkt G schneidet. Siehe Abbildung 10.2 Auch hier lassen sich die gesamten Koordinaten des Schnittpunktes G rein analytisch ermitteln. |
| Für die Funktionsgleichung einer Ellipse gilt : |
 |
| Für die y-Koordinate gilt: y = yG = yS |
| Einsetzen von yG in die Gleichung und Auflösung nach x liefert dann xG: |
 |
| 10.3 | Geozentrische und geographische Breite des Schnittpunktes |
|
|
|
| Aus der x und y Komponente lassen sich die geozentrischen Daten des Punktes G bestimmen. |
| Die geozentrische Breite ψ ist definiert durch: |  |
| Einsetzen von yG und xG in die Gleichung liefert die geozentrische Breite ψG des Punktes G |
 |
| Durch Umrechnung lassen sich dann schließlich die geographischen Daten des Punktes G ermitteln. |
| Der Zusammenhang zwischen geozentrischer Breite ψ und geographischer Breite φ ist definiert durch folgende Gleichung ( siehe auch 9.1): |
 |
| Einsetzen von tangens φyG in die Gleichung liefert die geographische Breite ψG des Punktes G |
 |
| 10.4 | Ein ausgezeichneter Breitengrad |
|
|
|
| Der Formfaktor fo schließlich, kann ja auch noch durch n, den Numerus der Abplattung dargestellt werden: |
 |
| Einsetzen von fo bzw. von n in die Gleichungen liefert dann die folgende Tabelle : |
| Numerus der Abplattung | geozentrische Breite | geographische Breite |
| n | φ | ψ |
| 296 | 29° 48‘ 15,92" | 29° 58‘ 19,06" |
| 297 | 29° 48‘ 18,29" | 29° 58‘ 19,40" |
| 298 | 29° 48‘ 20,64" | 29° 58‘ 19,73" |
| 299 | 29° 48‘ 22,98" | 29° 58‘ 20,07" |
| 300 | 29° 48‘ 25,30" | 29° 58‘ 20,40" |
Aus der Tabelle sind folgende Minimal-Maximal-Grenzen ersichtlich: für 296 ≤ n ≤ 300 gilt: 29 ° 58‘ 19,06" ≤ φ ≤ 29° 58‘ 20,40" Also
gilt für die Winkeldifferenz: Δ φ = 1,34" |
| Bezüglich der Ellipse
nimmt der Punkt G eine ausgezeichnete Position
ein. Er ist ein direkter Punkt auf der Ellipse, der in
einem eindeutigen Bezug zur Schmiegekreiskonstruktion
steht. Bezüglich
eines Rotationsellipsoiden würde aus dem Punkt G ein kompletter Breitenkreis
entstehen. Ausgehend von einem Rotationsmodell für die Erde, hätten wir hier sogar zwei ausgezeichnete Breitengrade vor uns mit: |
| φ 1 = +29° 58‘ 19-20,5" N φ 2 = -29° 58‘ 19-20,5" S |
| 10.5 | Ein weiterer ausgezeichneter Breitengrad |
|
|
|
| Genau genommen existieren zwei Schnittpnkte. Der zweite Punkt G2 entsteht dadurch, das die x-Koordinate, also die Parallele zur y-Achse, die Ellipse schneidet. | ||
 |
||
| Abbildung 10.3 - Zweiter Schnittpunkt | ||
| Für die x-Koordinate gilt: x = xG2= xS |
| Einsetzen von xS in die Ellipsen-Gleichung und Auflösung nach y liefert dann yG2: |
 |
| Einsetzen von yG2 und xG2 in die Gleichung liefert die geozentrische Breite φG2 des Punktes G2 |
 |
| Umrechnung liefert die geographische Breite φjG2 des Punktes G2 |
 |
| Ausgehend von einem Rotationsmodell für die Erde, hätten wir hier wiederum zwei ausgezeichnete Breitengrade vor uns: |
| φ 3 = +59° 58‘ 19-20,5" N φ 4 = -59° 58‘ 19-20,5" S |
| Bezüglich
der Ellipse nehmen die Punkte G und G2 ausgezeichnete
Positionen ein. Sie sind die einzigen direkten
Punkte auf der Ellipse, die in einem eindeutigen Bezug
zur Schmiegekreis-
Konstruktion stehen. (ausser dem Schnittpunkt der
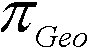
Schmiegekreisgeraden mit der Ellipse selber) Ausgehend von einem Rotationsmodell für die Erde, hätten wir insgesamt also vier komplette ausgezeichnete Breitengrade vor uns. Bildet man die Mittelwerte zwischen der grossen und der kleinen Achse einer Ellipse, so stehen diese Mittelwerte in Beziehung zur Schmiegekreis-Konstruktion bzw. den Punkten G und G2. Dieser Zusammenhang wird das Thema der nächsten Kapitel sein. |
