Es existieren verschiedene Mittelwerte, und zwar sind es das geometrische Mittel, das arithmetrische Mittel, das harmonische Mittel und das quadratische Mittel. An dieser Stelle betrachten wir zuerst nur das harmonische Mittel.

Für zwei Grössen a und b (z.B. die grosse und die kleine Achse einer Ellipse), aus denen der harmonische Mittelwert gebildet werden soll, gilt dann folgende Beziehung:

Das harmonische Mittel nimmt eine besondere Stellung bezüglich der Ellipse ein. Es existiert nämlich ein Zusammenhang mit der Schmiegekreis-Konstruktion.

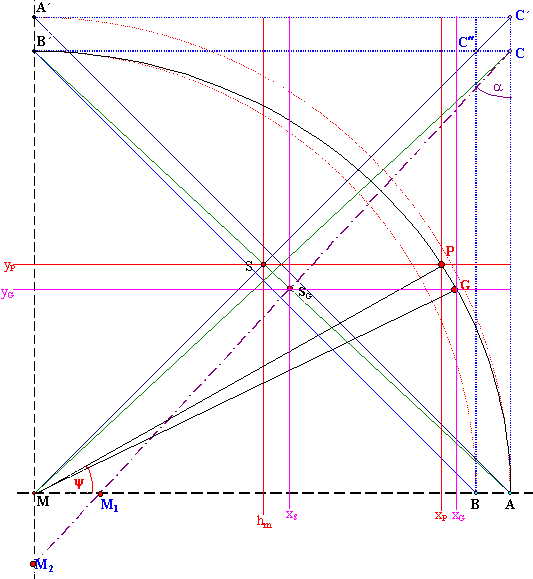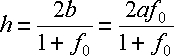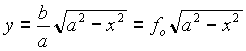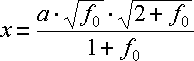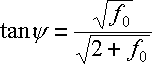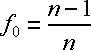
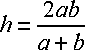
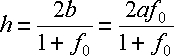
In Abbildung 11.1 sind die x und die y - Komponente des Punktes S das halbe harmonische Mittel zwischen den beiden Halbachsen a und b.

Es gilt: x_S = y_S = y_P = h/2 = h_m

Der Punkt S ist gleichzeitig auch der Schnittpunkt der (Ellipsen)Diagonalen AB' mit der Quadratdiagonalen MC'

Der Punkt S liegt wie der Punkt S_G auf der Diagonalen AB'. Wie in Kapitel10 schon mit dem Punkt S_G geschehen, kann der Punkt S auch hier auf die Ellipse übertragen werden. Und so entsteht der Punkt P, als Schnittpunkt der y-Koordinate (des Punktes S) mit der Ellipse.

Die Koordinaten des Schnittpunktes P lassen sich rein analytisch, also mathematisch, ermitteln. Die Ableitung für den Schnittpunkt geschieht folgendermassen:

Das harmonische Mittel für die beiden Halbachsen der Ellipse :

Für die Funktionsgleichung einer Ellipse gilt:

Aufgrund der geometrischen Konstruktion (Abb. 11.1) gilt für die y-Koordinate: y = y_P = h/2

Ersetzen von y durch h in der Funktionsgleichung und anschliessende Auflösung nach x liefert dann x_P:

Für die geozentrische Breite Ψ des Punktes P gilt: tanΨ = y/x = h/(2x)

Einsetzen der entsprechenden Terme in die Gleichung und anschliessende Kürzung liefert:

Der Formfaktor f_o schließlich, kann ja auch noch durch n, den Numerus der Abplattung dargestellt werden:

Lässt man n, also den Numerus der Abplattung, in 0,25er Schritten einen bestimmten Bereich durchlaufen, erhält man eine Tabelle von Breitenwinkeln. Der Bereich ist so gewählt, das alle geodätischen Systeme darin enthalten sind.