DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 3.2.0 | Genauigkeit der Winkel des Quadratur-Dreiecks 2 | |
| 3.2.1 | Die Näherung für die Kreis-Quadratur | |
| 3.2.2 | Das Seiten/Höhenverhältnis | |
| 3.2.3 | Die Differenz zwischen genauem und angenähertem Wert | |
| Wie im ersten Fall kann man im Fall der
Quadratur 2 die Winkel und auch die
Höhen/Seitenverhältnisse des Quadratur-Dreiecks
benutzen. Beginnen wir mit den Winkeln. Die Differenz zwischen genauem Wert und dem Näherungswert besitzt bei alpha und beta den gleichen Betrag nämlich: 0° 0´ 37,6" . Rechnet man dies prozentual auf die genauen Winkel um, so ergibt sich für alpha eine Ungenauigkeit von ± 0,0181 % und für beta eine Ungenauigkeit von ± 0,0321 %. Winkelmäßig gesehen ist die Ungenauigkeit also stets kleiner als eine Winkelminute, und prozentual gesehen bedeutet dies eine Ungenauigkeit, die 0,035% nicht überschreitet. Was sich als hinreichend genau, für die meisten vorkommenden Verhältnisse, bezeichnen läßt. Beim Zeichnen in der Größenordnung DINA3 oder DINA4 beträgt die Zeichengenauigkeit maximal 0,1 Grad, was 6 Winkelminuten entspricht. Damit hat die Quadratur-Ungenauigkeit keinen Einfluß auf die Zeichengenauigkeit, und ist in diesem Größenbereich daher unerheblich. |
| Die Quadratur-Konstruktion ist ja dazu gedacht, einen vorgegebenen Kreis in ein umfanggleiches Quadrat zu verwandeln. Da der Radius bekannt ist, entsteht für die Quadratseite daraus eine eindeutige Beziehung. Dies gilt auch, wenn für π die Näherungslösung eingesetzt wird und die entsprechende Gleichung lautet dann wie im ersten Fall: |
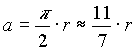 |
| Damit gelten alle Genauigkeitsbetrachtungen, die für die Quadratseite, im Falle der Konstruktion 1 (siehe dazu 2.2.2 und 2,2,3), gemacht worden sind, auch in diesem Fall. |
| Nimmt man also ein Schnitt-Dreieck und betrachtet darin die Höhe h und die Grundseite s, indem die Verhältnisse dieser Größen zueinander gebildet werden, so ergibt sich: |
| Für das Seiten/Höhenverhältnis des Schnitt-Dreiecks gilt |
| s:h = 2:π |
| Für die Näherung des Seiten/Höhenverhältnis gilt dann |
| s:h = 7:11 |
| Die Differenz zwischen genauem Wert und Näherungswert läßt sich zur Ungenauigkeitsbestimmung benutzen. |
| Δ s = (2/π - 7/11)h |
| Um einen Überblick der Abweichungen bei verschiedenen Größenverhältnissen zu erhalten, braucht man ja nur, wie oben schon geschehen, den Einheitsradius in 10er Schritten zu vergrößern. Aus Übersichtsgründen wurde auch hier die minimale Größe für den Radius des Grundkreises mit 10 cm angesetzt. |
| Höhe/Radius | Differenz = Näherung - wahrer Wert) |
| für die Grundseite des Schnitt-Dreieck | |
| 10 cm | 0,0256136 mm |
| 1 m | 0,256136 mm |
| 10 m | 2,56136 mm |
| 100 m | 2,56136 cm |
| 1km | 25,6136 cm |
| 10 km | 2,56136 m |
| 100 km | 25,6136 m |
Tabelle 5
| Bei der Berechnung der Differenz ergibt sich
ein positives Ergebnis, heißt also der Näherungswert
ist etwas zu klein geraten. Rechnet man die, in Tabelle 5 angegebenen, Differenzen prozentual auf die wahre Höhe des Schnitt- Dreicks (bzw. dem Radius des Kreises) um, so erhält man einen Fehler von ± 0,04 %, für alle auftretenden Fälle. Aus der Tabelle 5 im Vergleich zu Tabelle 2 ist ersichtlich, das die vorkommenden Fehlergrößen nur die Hälfte des Quadratseiten-Fehlers ausmachen. Damit gelten alle Genauigkeitsbetrachtungen, die für die Quadratseite gemacht worden sind, auch in diesem Fall. |