 |
DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
|
| 3.1.0 | Die Quadratur des Kreises 2 |
 |
 |
 |
 |
Es existiert, wie weiter oben schon
erwähnt, eine weitere Quadratur-Konstruktion, die
Umfangsgleichheit liefert, und mit einem Dreieck ABC (siehe dazu
Abbildung 3) realisiert wird, das nicht nur ein anderes
Höhen / Seiten - Verhältnis besitzt, sondern auch in
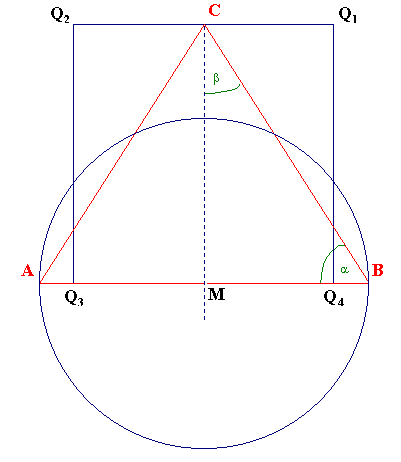
der Gesamt-Konstruktion abweicht. Die Höhe des Dreiecks ist hier gleich einer Quadratseite. Die Grundseite des Dreiecks ist gleich dem Durchmesser des Kreises. Dieses Dreieck ABC wird hier in der Folge als Quadratur-Dreieck 2 bezeichnet. |
|
| Abbildung 3 - Die Quadratur des Kreises 2 |
| 3.1.1 | Definition der Strecken der Quadratur-Konstruktion 2 |
|
|
|
| Es müssen auch hier erst einmal einige Definitionen bezüglich der vorkommenden Strecken, anhand Abbildung 3, getätigt werden. |
|
||||||||||||||||||||
| 3.1.2 | Die Quadratur-Bedingung |
|
|
|
| Kreis und Quadrat besitzen gleichen Umfang : |
|
| 3.1.3 | Das Verhältnis für die Seiten |
|
|
|
 |
| 3.1.4 | Das Verhältnis für die Winkel |
|
|
|
  |
| 3.1.5 | Die Näherung für Pi |
|
|
|
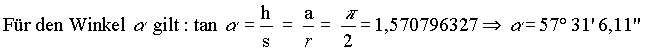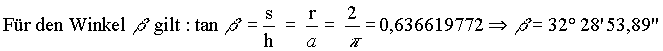| Die bisherigen Betrachtungen sind, wie bei
der Kostruktion 1 mathematisch exakt. In der praktischen
Konstruktion aber, wie in Abbildung 3 dargestellt, ist
dies durch Zirkel und Lineal ebenfalls nicht lösbar.
Für die geometrische Konstruktion müssen die einzelnen
Längen erst durch eine Rechnung ermittelt werden. Auch hier läßt sich dieser Umstand vereinfachen, wenn für π eine Näherung benutzt wird. Wie im vorherigen Fall, also der Quadratur 1, besteht die einfachste Annäherung an π mit Hilfe eines Teiles der archimedischen Ungleichung: |
 |
| 3.1.6 | Die Näherung für die Seiten |
|
|
|
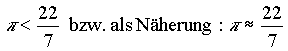| Für die Gesamtkonstruktion bzw. das Quadratur-Dreieck ergibt sich dann folgendes Verhältnis: |
 |
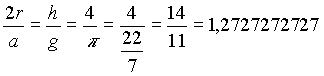| Für das Höhen/Seitenverhältnis der Schnitt-Dreiecke gilt |
| h:s = 11:7 |
| 3.1.7 | Die Näherungen für die Winkel |
|
|
|
| Für die Winkel gilt mit dieser Näherung: |
  |
| 3.1.8 | Das zweite Quadratur-Dreieck |
|
|
|
 |
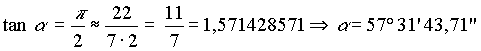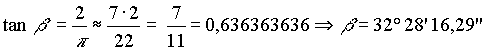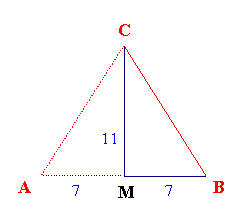Nimmt man also ein rechtwinkliges Dreieck,
(in Abbildung 3 bzw. 4 entsprechend den Schnitt-
Dreiecken MBC bzw. MAC) mit dem Höhen/Seiten - Verhältnis 11:7, so läßt sich
daraus auch die komplette Quadratur aus Abbildung 3
ableiten. Aus Abbildung 4 wird erkenntlich, wie mittels eines Schnitt-Dreieckes und dessen Entwicklung, durch Spiegelung, das Quadratur-Dreieck 2 erzeugt wird. Der nächste Schritt wäre die weitere Entfaltung in die Gesamtkonstruktion 2. |
|
| Abbildung 4 - Das Quadratur-Dreieck 2 | ||
| Somit steht eine zweite Technik zur Verfügung, die es gestattet einen Kreis in ein umfanggleiches Quadrat, auf geometrischen Wege, zu transformieren. | ||
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |
