 |
KRITERIEN ZUR GEOMETRIEBESTIMMUNG IN LANDSCHAFTEN
Copyright © Klaus Piontzik
| Außer Linienbildung existieren noch die
regelmäßigen Abstands-und Winkelteilungen als
Grundbeziehungen. Mehrere Objekte können gleiche Abstände von einander besitzen. Wie bei der Linienbildung sind auch hier mindestens drei Punkte erforderlich, die dann zwei gleiche Abstände erzeugen. Dies könnte man so formulieren: Eine regelmäßige Abstands-Teilung muß durch mindestens drei Punkte, und zwei gleichen Abständen zwischen diesen Punkten, gekennzeichnet sein. Zwei Abstände können aber auch hier lediglich durch eine Symmetrie erfüllt werden. Je mehr Objekte mit gleichem Abstand vorhanden sind, umso größer ist die Wahrscheinlichkeit einer regelmäßigen Teilung. Eine Verschärfung des Kriteriums läßt sich auch hier durch eine Erhöhung der Punkt- und der Abstandsanzahl erreichen. |
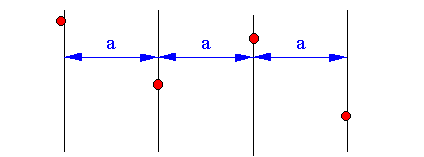
| K5 | Eine einfache regelmäßige Abstands-Teilung muß durch mindestens vier Punkte und drei gleichen Abständen a gekennzeichnet sein |
 |
| Der Einfachheit halber wird künftig nur
noch von Abstands-Teilungen die Rede sein,
wenn eine einfache regelmäßige Abstandsteilung
vorliegt. Bei der Konstruktion von Abstandsteilungen kann sich folgende, oder auch eine ähnliche, Situation ergeben: |
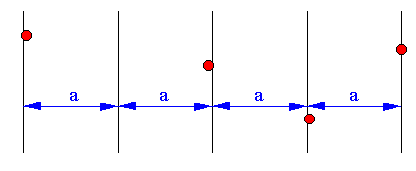 |
| Hier verbleibt eine Teilung ohne
Punkt. Egal aus welchen Gründen ein oder mehrere Orte
unbelegt bleiben, die Teilung erfüllt in jedem Fall das
Kriterium 5. Es wurde ja nicht gefordert, das die Punkte aufeinander folgend angeordnet sein müssen. Der Abstand bleibt bei der obigen Konstruktion invariant, und man erhält ja sogar noch einen Abstand mehr, als in Kriterium 5 gefordert. Daher können, ohne Beschränkung der Allgemeinheit, auch solche Abstandsteilungen benutzt werden, deren Teilungslinien nicht vollständig belegt sind. Zu beachten ist noch der Umstand, das die Punkte selber nicht unbedingt auf einer Linie liegen müssen. Tun sie es doch einmal, so haben wir eine besondere Art der Abstandsteilung erhalten, nämlich: |
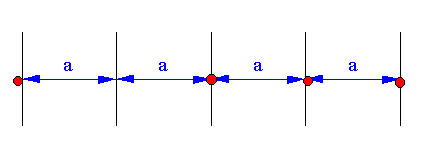
| 5.1 - Definition | Eine einfache regelmäßige Abstands-Teilung, deren Punkte alle auf einer Linie liegen, heißt lineare Unterteilung |
 |
| Eine typische Anwendung der linearen
Unterteilung ist die ständige Halbierung einer Strecke.
Die daraus enstehende Abstandsteilung besitzt die kleinste vorkommende Halbierungsstrecke als Abstand a. Das sieht dann so aus: |
 |
| Allgemein lassen sich durch lineare
Unterteilungen beliebige ganzzahlige
Teilungsverhältnisse darstellen. Umgekehrt bieten
lineare Unterteilungen aber auch die Möglichkeit
ganzzahlige Vielfache von Strecken abzubilden. Lineare
Unterteilungen eigenen sich damit vorzüglich zur
Beschreibung von Proportionen. Zeichnet man nur die Punkte ein, ergibt sich folgendes Bild: |
 |
| Hieran kann man erkennen, das sich das
Vorhandensein einer linearen Unterteilung nicht
feststellen läßt, wenn nur die Punkte allein betrachtet
werden. So ist auch nachvollziehbar, mit welch einfachen
Methoden selbst lineare Zusammenhänge verschleiert
werden können. Mit Hilfe der Abstandsteilungen kann noch
eine weitere wichtige Anwendung abgeleitet werden,
nämlich die so genannten Gitter. |
| Außer Abständen (Strecken) lassen sich
auch Winkel zur Geometrienbildung benutzen. Das Kriterium
für Abstandsteilungen läßt sich nämlich auf Winkel
anwenden. Regelmäßige Winkelteilungen werden bei der Konstruktion von Vielecken benötigt, also Figuren die 5,6,7 oder mehr Ecken und Seiten besitzen. Wie bei den Abständen können drei Punkte, mit zwei Winkeln dazwischen, lediglich eine Symmetrie bzw. ein Dreieck oder auch Teil eines Vierecks darstellen. Auch hier muß eine Verschärfung erfolgen, so das ein Kriterium für Winkelteilungen also lautet: |
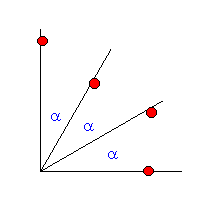
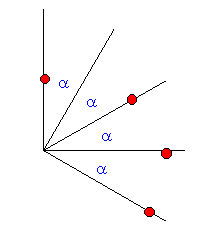
| K6 | Eine einfache regelmäßige Winkel-Teilung muß durch mindestens vier Punkte, und drei gleiche Winkel alpha gekennzeichnet sein |
 |
| Genau wie bei den Abstandsteilungen, brauchen nicht alle Teilungsachsen belegt zu sein. D.h. Beispiele wie das hier Folgende können uneingeschränkt für Nachweise benutzt werden. |
 |
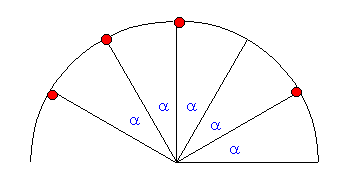
| Ähnlich der linearen Unterteilung bei den Abstandsteilungen, können bei Winkelteilungen alle Punkte auf einem Kreisradius angeordnet sein. Sie besitzen also gleichen Abstand vom gegebenen Zentrum aus. |
| 6.1 - Definition | Eine regelmäßige Winkel-Teilung, deren Punkte gleiche Abstände vom Zentrum besitzen wird als Kreisteilung bezeichnet |
 |
|
252
Seiten, davon 116 in Farbe 163 Bilder Herstellung
und Verlag: ISBN 9783755742111 Ladenpreis: 24 Euro |