 |
KRITERIEN ZUR GEOMETRIEBESTIMMUNG IN LANDSCHAFTEN
Copyright © Klaus Piontzik
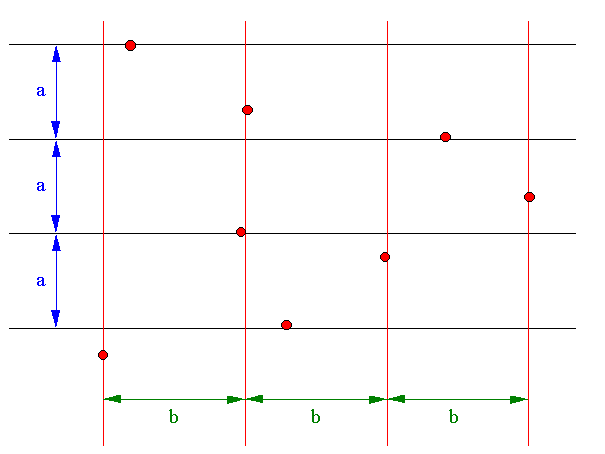
| Mit Hilfe der Abstandsteilungen kann noch eine weitere wichtige Anwendung abgeleitet werden, nämlich die so genannten Gitter. Liegt z.B. eine Abstands-Teilung in waagerechter Richtung vor, und existiert dazu auch in senkrechter Richtung eine andere Abstandsteilung, so läßt sich, mit den beiden gegebenen Abständen als Grundseiten, ein rechteckiges Gitter erzeugen. |
 |
| Die beiden Abstands-Teilungen brauchen nicht
unbedingt senkrecht aueinander zu stehen, sondern können
sich auch unter einem bestimmten Winkel schneiden. Ebenso
brauchen die beiden Teilungen nicht unbedingt in
senkrechter oder horizontaler Richtung zu verlaufen. Sie
können auch in einem beliebigen Winkel zum
(kartesischen) Bezugssystem liegen. Aufgrund dieser Umstände müssen einige Begriffserklärungen bezüglich der konstruierbaren Gitter getätigt werden. In Anlehnung an die Geometrie, lassen sich daher folgenende Definitionen aufstellen: |
| K7 | Ein affines rechteckiges Gitter liegt vor, wenn zwei regelmäßige Abstands-Teilungen existieren, die nicht parallel zu einander verlaufen |
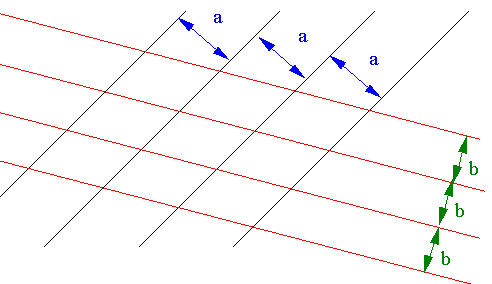 |
| Dieses ist die allgemeinste Form eines affinen Gitters. Alle anderen Gittertypen lassen sich als affine Gitter mit bestimmten Eigenschaften beschreiben. |
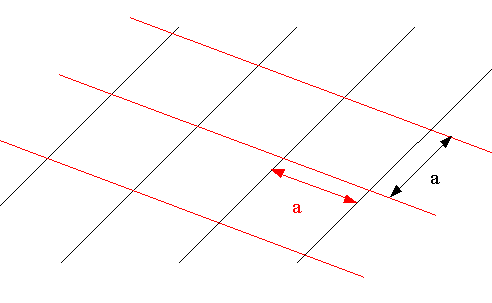
| 7.1 - Definition | Ein affines Gitter heißt quadratisch, wenn die beiden Abstands-Teilungen gleiche Abstände besitzen |
 |
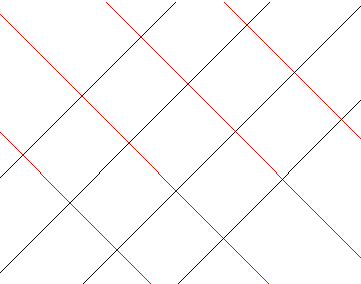
| 7.2 - Definition | Ein affines Gitter heißt orthogonal, wenn die beiden Abstands-Teilungen senkrecht auf einander stehen |
 |
| 7.3 - Definition | Ein affines Gitter heißt kartesisch, wenn es orthogonal ist, und die beiden Abstandsteilungen in horizontaler und in vertikaler Richtung verlaufen |
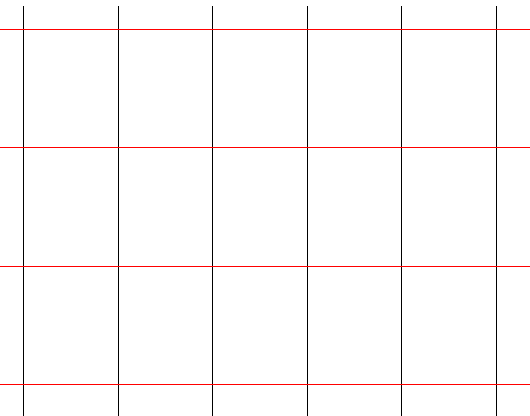 |
| Mit diesen Definitionen lassen sich quasi
alle Gitter, die möglich sind, klassifizieren. Die
meisten, ebenfalls die in dieser Studie gefundenen,
Gitter kann man als affine, quadratische, orthogonale
Gitter bezeichnen. Kartesische Gitter sind, nach Definition, auch immer orthogonale Gitter. Die Längen- und Breitenkreise, die zur Angabe der geographischen Koordinaten dienen, werden hier als kartesisches Gitter benutzt. Die Breitenkreise bilden dabei die horizontale Ausrichtung und die Längenkreise stehen für die vertikale Ausrichtung. Zu jedem
Gitter existiert aber auch ein entsprechendes
Diagonalgitter. Einerseits kann man dies geometrisch
begründen, andererseits gibt es historische bzw.
geomantische Gründe. |
| 7.4 - SATZ | Jedes Gitter läßt sich durch ein entsprechendes Diagonalgitter erweitern oder auch ersetzen |
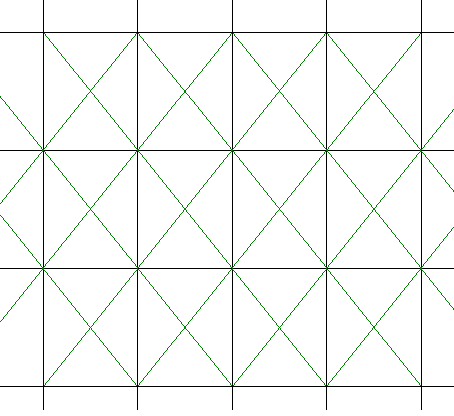 |
| In der Zeichnung ist zu erkennen, das das Diagonalgitter nicht orthogonal verläuft, obwohl das zugrunde liegende Gitter diese Qualität besitzt, ja sogar kartesisch ist. Um orthogonale Diagonalgitter zu erhalten bedarf es nämlich folgender Eigenschaft: |
| 7.5 - SATZ | Ein Diagonalgitter ist dann orthogonal, wenn das zugrunde liegende Gittersystem quadratisch ist |
| Und nur eine ganz bestimmte Gruppe von Gittern erzeugt Diagonalgitter, die nicht nur orthogonal, sondern auch quadratisch sind: |
| 7.6 - SATZ | Nur quadratische, orthogonale Gitter erzeugen ebenfalls quadratische, orthogonale Diagonalgitter |
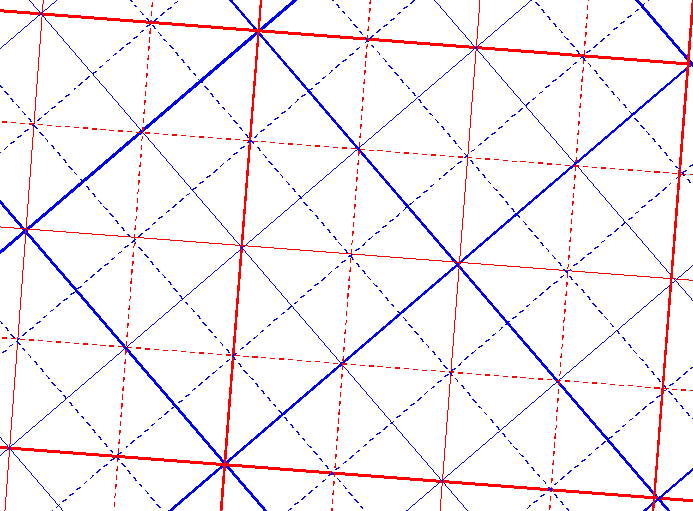 |
| Auf der Grundlage der bisherigen Betrachtungen, läßt sich jetzt eine Schreibweise für Gittersysteme einführen. Die durch Objekte (Punkte) gebildeten Systeme, die als Bezugssysteme dienen, kann man z.B. als Grundsysteme benutzen. Ebenso das geographische Koordinatensystem. |
| 7.7 - Definition | Gitter die als Bezugssysteme benutzt werden heißen Grundgitter |
| 7.8 - Schreibweise | Gitter G <=> #G |
| Die Eigenschaften der Gitter lassen sich dann mit kleinen Buchstaben darstellen, die einfach hinten die bisherige Bezeichnung geschrieben werden: |
| 7.9 - Schreibweise | Eigenschaften der Grundgitter |
| a) Gitter G ist quadratisch <=> #Gq |
| b) Gitter G ist orthogonal <=> #Go |
| c) Gitter G ist kartesisch <=> #Gk |
| Treten mehrere Eigenschaften auf, so werden
auch diese einfach hinter einander gesetzt. Im Grunde
kommen ja lediglich die Kombinationen qo und kq
in Frage. In dieser Untersuchung wird als kartesisches Grundsystem das geographische System benutzt, mit der geographischen Länge Lambda und der geographischen Breite Phi. Dieses System erhält jetzt einen Eigennamen. Hauptsächlich aus Vereinfachungs-und Übersichtsgründen. |
| 7.10 - Schreibweise | kartesisches geographisches Grundsystem |
| Gitter ist kartesisches geographisches Grundsystem <=> Lambda-Phi # |
| wird gelesen: Lambda-Phi-Gitter |
| Dadurch braucht man bei den geographischen
Systemen nur noch zwischen rechteckigen und quadratischen
Systemen zu unterschieden. Laut obiger Definition der
Eigenschaften von Gittern, ist es dann auch hinreichend,
lediglich die quadratischen Systeme zu kennzeichnen, und
zwar mit: Lambda-Phi #q Außer den Grundgittern existieren auch noch Systeme, die sich aus dem Grundgitter heraus erzeugen lassen.Wie das Diagonalsystem. Solche Gittersysteme heißen dann erzeugte Systeme. |
| 7.11 - Definition | Gitter die aus einem Grundgitter ableitbar sind, heißen erzeugte Gitter |
| 7.12 - Schreibweise | Lambda-Phi # erzeugt Gitter G <=> Lambda-Phi #(G) |
| Mit einem quadratischen Lambda-Phi -Gitter als Grundgitter ( Lambda-Phi #q ), lassen sich quasi alle anderen Gitter als erzeugte Gittersysteme darstellen. |
|
252
Seiten, davon 116 in Farbe 163 Bilder Herstellung
und Verlag: ISBN 9783755742111 Ladenpreis: 24 Euro |