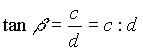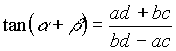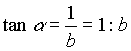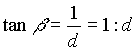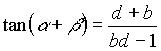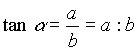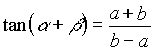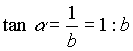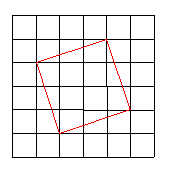
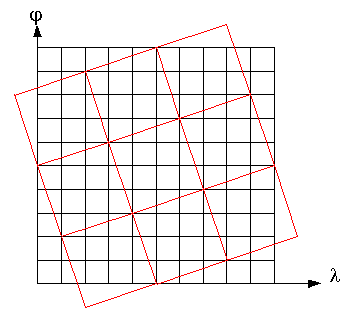
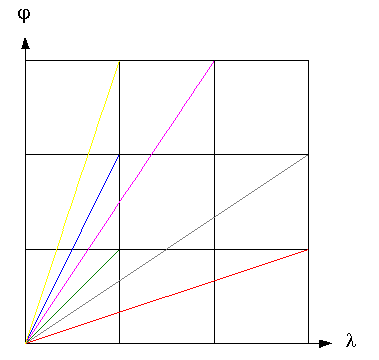
KRITERIEN ZUR GEOMETRIEBESTIMMUNG
IN LANDSCHAFTEN
© Klaus Piontzik
Erzeugte Gitter
 |
In einem
gegebenen Gitter kann man beliebig liegende Strecken als Teilungsverhältnisse
der Gitterseiten ausdrücken. Besonders einfache Gestalt erhält man, wenn ganzzahlige Proportionen benutzt werden. Das sieht dann so aus wie in der nebenstehenden Abbildung |
| Für die Teilungsverhältnisse der einzelnen Strecken ergeben sich so folgende Zusammenhänge: |
| Farbe | Seiten-Verhältnis |
| gelb | 3:1 |
| blau | 2:1 |
| magenta | 3:2 |
| grün | 1:1 |
| grau | 2:3 |
| rot | 1:3 |
| allgemein | Phi:Lambda |
allgemein |
y:x |
| Genau
genommen gibt das Teilungsverhältnis ja den Tangens des Winkels an, den die Strecke
mit der Lambda-Achse bildet. Für die rote Strecke gilt
demnach: tan Winkel = 1:3 => Winkel = 18,4349° Der Sachverhalt ist hier identisch mit Funktionen, die in einem xy-System dargestellt werden. Das Teilungsverhältnis steht demnach auch gleichzeitig für das Steigungsverhältnis y:x der Strecke. |
 |
 |
|
| Nimmt man nun diese Strecke als Grundseite und konstruiert daraus ein Quadrat, so ergibt sich das obere Bild | Aus dem Quadrat kann man jetzt auch ein komplettes Gitter erzeugen. |
| Mit dem Steigungsverhältnis y:x und der Schreibweise für erzeugte Gitter, läßt sich das rote Gitter im Lambda-Phi #-System z.B. so darstellen: |
| #G = Lambda-Phi #(Phi:Lambda) = Lambda-Phi #(1:3) |
 |
Wird in
einem Grundgitter ein weiteres Gitter erzeugt, so gibt es
stets zwei Möglichkeiten dieses neue
Gitter anzulegen. In der nebenstehenden Abbildung ist das blaue Gitter das Grundgitter und das rote Gitter ist das zugehörige Diagonalgitter. Das dunkelgrüne Gitter ist dann ein 1:2-Gitter und das hellgrüne Gitter ist das zweite Gitter. Der rot-markierte Punkt dient als Ausgangspunkt der Erzeugung für die grünen Gitter. |
|
| Sind,
ausser den Winkelwerten im Lambda-Phi #-System, die Abmaße x,
y des Grundgitters bekannt, so läßt sich,
anhand des Satzes von Pythagoras, auch die Länge der
erzeugten Strecke s² = x²+y² bestimmen. Da die Gitterseiten s aber auch andere Längen besitzen können als die durch die Konstruktion vorgegebene, müssen für eine allgemeine Definition noch diese Gitterlängen berücksichtigt werden. |
| Schreibweise | erzeugte Gitter |
| Lambda-Phi # erzeugt #G mit Steigungsverhältnis y:x = tan a und Gitterlänge s |
| #G = Lambda-Phi #(y:x, s) = Lambda-Phi #(tan a , s) |
| Ist die Gitterlänge s² = x²+y² heißt also durch das Steigungsverhältnis und das Grundgitter eindeutig festgelegt, so kann die Gitterlänge weggelassen werden. |
| Lambda-Phi # erzeugt #G mit Steigungsverhältnis y:x und Gitterlänge s² = x²+y² |
| #G = Lambda-Phi #(y:x) |
| Ist das zugrundeligende Gitter selbst ein erzeugtes Gitter z.B. im Lambda-Phi #-System, so ergibt sich folgende Schreibweise für das Diagonalgitter: |
| Schreibweise | Diagonalgitter eines erzeugten Gitters |
| #D = Lambda-Phi #(G(d)) = Lambda-Phi #(G)(d) = Lambda-Phi #(y:x)(d) |
| Die hier eingeführte Schreibweise reicht aus, um alle anfallenden Gitter beschreiben zu können. |
Summen von Winkeln
| Winkel
werden häufig durch die Seitenverhältnisse eines
zugrunde liegenden Dreiecks angegeben. In der Regel
entspricht dieses Verhältnis dem Tangens des Winkels. Sollen nun zwei Winkel addiert werden, so kann dies über die Additionstheoreme der Trigonometrie geschehen. Die entsprechende Gleichung lautet: |
 |
| Da der Tangens in der Regel als Bruchdarstellung vorliegt, ist hier eine Vereinfachung möglich. |
| Es sei |  |
und |  |
| Einsetzen der Brüche in die obige Gleichung, Bildung des Hauptnenners und anschließende Kürzung, ergibt dann folgende Formel: |
 |
| Für den Fall das a = c = 1 gilt dann für das Tangensverhältnis: |
| Es sei |  |
und |  |
| Damit ergibt sich folgende Vereinfachung: |  |
Gitter und Winkel
| Wenn Gittersysteme vorliegen, wird zu einem erzeugten Gitter oft das zugehörige Diagonalgitter gesucht. Dabei wird zum Grundwinkel des erzeugten Gitters 45 Grad hinzugefügt. Der Tangens für 45 Grad ist aber gleich eins. |
 |
und | tan b = 1 |
| Einsetzen der Brüche in die Summengleichung, Bildung des Hauptnenners und anschließende Kürzung, ergibt dann folgende Formel: |
 |
| Für den Fall das a = 1 gilt dann für das Tangensverhältnis: |
| Es sei |  |
und tan b = 1 |
| Damit ergibt sich folgende Vereinfachung: |  |
| Seitenverhältnis des erzeugten Gitters | Seitenverhältnis des Diagonalgitters |
| 1:2 | 3:1 |
| 1:3 | 2:1 |
| 1:4 | 5:3 |
| 1:5 | 3:2 |
| 1:6 | 7:5 |
| 1:7 | 4:3 |
| 1:8 | 9:7 |
| 1:9 | 5:4 |
| 1:10 | 11:9 |
