Energetik

Energieformen und Seinsformen

Copyright © Klaus Piontzik


1.5 – REIZERFASSUNG

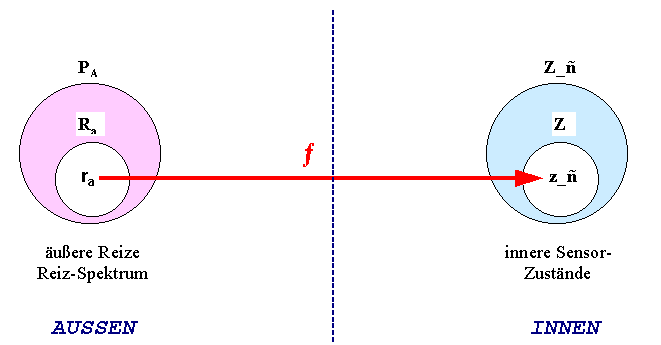
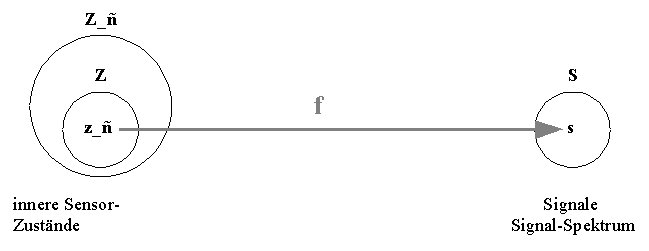
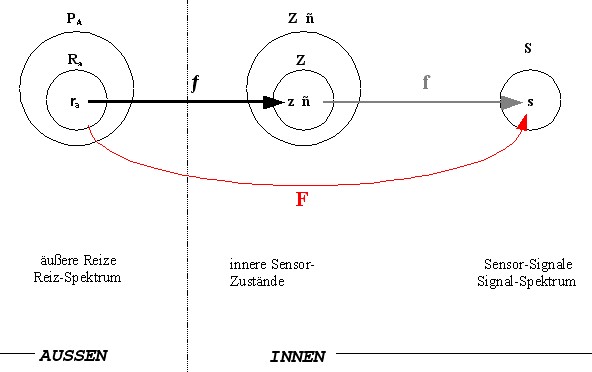
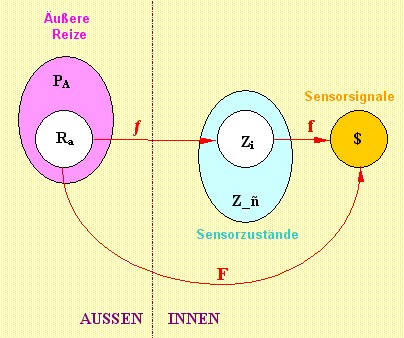
1.5.1 DEFINITION: Reizerfassungs-Funktion

Sensorensysteme, egal ob natürliche oder technische, lassen sich in ihrer Funktion durch die zugehörigen Zustandsräume beschreiben. Da die inneren Zustände durch äußere Reize verursacht werden, stellen die Zustandsräume mithin die maximalen Erfassungsräume eines Sensorsystems dar.

Mathematisch gesehen läßt sich dieser Zusammenhang als Abbildung (Funktion) beschreiben. Es werden jedem Element einer Menge ein Element einer anderen Menge zugeordnet. In diesem Fall wird einem äußeren Reiz ra einem innerer Zustand z eines Sensors ñ zugeordnet.
Der äußere Reiz verursacht ja den inneren Zustand. Da aber nicht alle äußeren Reize in innere Sensorzustände umgewandelt werden, muß die Betrachtung auf eine gewisse Teilmenge der äußeren Reize eingeschränkt werden. Und zwar auf die Menge der registrierten äußeren Reize (Signale). Also die äusseren Signale, die auch innere Elementarsensor-Zustände erzeugen. Diese Zuordnung heißt dann Reizerfassungs-Funktion.


PA sei die Gesamtmenge der sensorisch registrierbaren äußeren Signale

Ra sei eine Menge äußerer Reize mit Ra ist echte Teilmenge von PA und ra ist Element von Ra

Z_ñ sei das Zustandsspektrum eines Sensors ñ und z_ñ ist Element von Z_ñ

Es sei Z Teilmenge (oder gleich) von Zustandsspektrum Z_ñ


Dann sei ƒ eine Abbildung mit folgenden Eigenschaften :

a) ƒ : Ra ---> Z Teilmenge (oder gleich) von Z_ñ

b) ƒ(Ra) = Z Teilmenge (oder gleich) von Z_ñ

c) ƒ(ra ) = z_ñ


ƒ heißt die Reizerfassungs-Funktion des Sensors ñ

Ra heißt dann Reizspektrum des Sensors ñ

Reizerfassungs-Funktion

Abbildung 1.5.1 - Reizerfassungs-Funktion ƒ



Aus der Abbildung ƒ wird ersichtlich, das Sensoren quasi die Schnittstelle (Interface) zwischen Innen und Aussen bilden.
Es existiert zwar eine Abbildung von den äußeren Reizen auf die Sensorzustände, mit ƒ(ra) = z_ñ
Reize ra und Zustände z_ñ sind aber nicht identisch, also Ra # Z_ñ

 

1.5.2.1 - SATZ

a) Es existiert keine direkte sensorische Erfassung der äußeren Welt.

b) Sensor-Zustände sind lediglich erstes Abbild der Außenwelt.

Durch den sensorisch registrierbaren Reizraum ist der maximale äußere Erfassungsraum eines Sensorsystems definiert.
Alle erfassten äußeren Reize sind inneren Sensor-Zuständen zugeordnet, und werden dadurch ja erst registrierbar. Aufgrund der Bijektion gilt auch die Umkehrung.


1.5.2.2 - Bemerkung

 Mit ƒ(Ra) = Z Teilmenge von Z_ñ wird garantiert, das alle erfassten äußeren Reize auch inneren Sensor-Zuständen zugeordnet werden. Und dadurch werden äußere Reize ja erst registrierbar.

Durch Z Teilmenge von Z_ñ wird berücksichtigt, das es innere Zustände geben kann,die nicht von äußeren Signalen erzeugt werden, z.B. durch Übersprechen anderer Kanäle oder erzeugt durch andere auftretende innere Effekte.
Durch ƒ(ra) = z_ñ wird die eindeutige Zuordnung eines äußeren Reizes zu einem inneren Sensor-Zustand sichergestellt.

Genaugenommen wirkt der äußere Reiz zum Zeitpunkt t auf den Sensor ein, und der innere Zustand stellt sich nach der Verzögerungszeit Te ein.

Es gilt dann ƒ(ra(t)) = z_ñ(t+Te)

Die Verzögerungszeit Te heißt Erfassungszeit.

 

1.5.3.1 - DEFINITION: registrierbarer Reiz

 Ein äusserer Reiz ra heistt sensorisch registrierbar, wenn er einen inneren Zustand z in einem Elementarsensor ñ erzeugt.

SCHREIBWEISE:

ƒ(ra) = z_ñ <=> ra->z_ñ <=> Reiz ra registriert durch z_ñ



1.5.3.2 - DEFINITION: registrierbares Reizspektrum

 Die Menge äusserer Reize Ra die das Zusatndsspekrtum Z_ñ erzeugen, heisst das sensorische Reizspektrum des Sensors n.

SCHREIBWEISE:

ƒ(Ra) = Z_ñ <=> Ra->Z_ñ <=> Reizspektrum Ra registriert durch Z_ñ



1.5.3.3 - DEFINITION: registrierbarer Reizraum R(N) einer Sensorenmenge N

 Ñ sei eine endliche Menge von Elementar-Sensoren mit ñ ist Element von Ñ

<Zn>_ñ sei der zugehörige Zustandsraum der Sensoren von Ñ

Die (Vereinigungs)Menge aller Reizspektren Ra der Sensoren von Ñ heißt der sensorisch registrierbare Reizraum R(Ñ) der Sensorenmenge Ñ

R(Ñ) = {Ra| ƒ(Ra) = Z_ñ und ñ ist Element von Ñ}

Reizraum


1.5.3.4 - SCHREIBWEISE

 R(Ñ) <=> <R>_>Ñ <=> die Reizmengen R von Ñ registriert

<R1...Rn>_>Ñ <=> R1 bis Rn von Ñ registriert


1.5.3.5 - BEZEICHNUNG

 <R1...Rn>_>Ñ = <Rn>_>Ñ heißt auch n-dimensionaler Reizraum der Sensoren von Ñ


Durch den sensorisch registrierbaren Reizraum ist der maximale äußere Erfassungsraum eines Sensorsystems definiert.

Alle erfassten äußeren Reize sind inneren Sensorzuständen zugeordnet, und werden dadurch ja erst registrierbar. Aufgrund der Bijektion gilt auch die Umkehrung.

1.5.3.6 - SATZ

Nur das ist registrierbar, für das es auch einen entsprechenden Elementar-Sensor gibt.

 

1.5.4 - SIGNALUMFORMUNG

 Die nächste Stufe in der Signalverarbeitung ist die Umformung der inneren Zustände z des Elementar-Sensors n in ein Signal s, das als Quelle für beliebige Informanten dienen kann. Die Transformation erfolgt in der Umformungseinheit ú.
Auch hier läßt sich der Begriff der Abbildung anwenden. In diesem Fall wird einem inneren Sensor-Zustand z ein internes Informationssignal s zugeordnet.
Da aber unter Umständen nicht alle inneren Sensor-Zustände umgewandelt werden, muß die Betrachtung auf eine gewisse Teilmenge eingeschränkt werden. Und zwar auf die Menge der ausgesandten inneren Signale. Also die inneren Elementarsensor-Zustände die auch wirklich Systemsignale erzeugen. Diese Zuordnung heißt dann Zustandsumformungs-Funktion.


1.5.4.1 DEFINITION : Umformungs-Funktion f einer Umformungseinheit ú

 Z_ñ sei das Zustandsspektrum eines Elementarsensors n mit z_ñ ist Element von Z und Z ist Teilmenge von Z_ñ

S sei die Menge der Signale die die Umformungseinheit ú erzeugt und s ist Element von S


Dann sei f eine Abbildung mit folgenden Eigenschaften :

a) f: Z --> S

b) f(Z) = S

c) f(z_ñ) = s


f heißt Zustandsumformungs-Funktion der Umformungseinheit ú
S heißt Signalspektrum der Umformungseinheit ú

Zustandsumformungs-Funktion

Abbildung 1.5.2 - Zustandsumformungs-Funktion f


1.5.4.2 - Beispiele

 1) Da technische Sensoren meistens ein digitales Signalspektrum besitzen, genügt hier eine elektrische Spannung um das Spektrum abzudecken. Benutzt werden in der Regel 12 V oder 24 V.
Das Signalspektrum besteht dann aus den Zuständen Spannung vorhanden und Spannung nicht vorhanden.


2) Sensoren mit analogem Signalspektrum arbeiten ebenfalls mit Spannungen, die dann allerdings in einem jeweils festgelegten Spannungsbereich variieren können. Die Bandbreite der abgegebenen Spannung ist in der Regel durch die physikalische Struktur des Sensors bedingt.

Analog-Sensor Signalspektrum
   
Dehnungsmeßstreifen 0...40 µV
Kohle-Mikrofon 0...100 mV
Piezo-Kristall 0...1 V
Thermoelement 0...40 mV



3)Sensoren Hg-Thermometer, Maßstab und Messbecher besitzen als Signalspektrum eine optische Eigenschaft: die der ablesbaren Länge und gehören damit auch zu den Analog-Sensoren.

Sensor Signalspektrum
   
Hg-Thermometer 0...Gesamtlänge
Maßstab 0...Gesamtlänge
Messbecher 0...maximale Füllhöhe



4) Bei Organismen, die ein höheres Nervensystem mit Zentralverarbeitung entwickelt haben, findet man als jeweiliges Signalspekrum der Sensoren eine Menge von chemo-elektrischer Impulsen, die pro Zeiteinheit abgegeben werden. Sie gehören also zu den Sensoren mit diskretem Signalspektrum.


Dann heißt die Komposition eines Elementar-Sensors ñ und einer Umformungseinheit ú einfacher kompletter Sensor n*

 

1.5.5.1 - DEFINITION : einfacher kompletter Sensor n*

 PA sei die Gesamtmenge der sensorisch registrierbaren äußeren Signale
Ra sei eine Menge (einwirkender) äußerer Reize mit Ra Teilmenge von PA und ra Element von Ra
Z_ñ sei das Zustandsspektrum eines Elementar-Sensors ñ und z_ñ Element von Z_ñ

Es sei Z Teilmenge von Z_ñ
ƒ sei eine bijektive Reizerfassungs-Funktion mit ƒ : Ra --> Z Teilmenge von Z_ñ und ƒ(ra) = z_ñ
Es gilt ƒ(Ra) = Z Teilmenge von Z_ñ

S sei die Menge der Signale die die Umformungseinheit ú erzeugt und s Element von S
f sei eine bijektive Zustandsumformungs-Funktion mit f : Z --> S und f(z_ñ) = s
Es gilt f(Z) = S

Dann heißt die Komposition eines Elementar-Sensors n und einer Umformungseinheit ú einfacher kompletter Sensor n*.


1.5.5.2 - SCHREIBWEISE: n* = ñ · ú (gelesen: n* ist gleich n verknüpft mit ú)

 Es gilt :

a) f · ƒ : Ra -->Z --> S

b) (f · ƒ)(Ra) = f(ƒ(Ra)) = S

c) (f · ƒ)(ra) = f(ƒ(ra)) = s



Die Komposition f · ƒ läßt sich durch eine einzelne Abbildung ersetzen, die dann aber auch alle Eigenschaften der Komposition besitzen muß.
Aus einer mehr technischen Sichtweise heraus sind andere Bezeichnungen für eine Komposition aus Funktionen noch Hintereinanderschaltung bzw. Reihenschaltung, oder auch Serienschaltung der Funktionen.


1.5.5.3 - DEFINITION: Übertragungungs-Funktion F eines Sensors n*

 n* sei ein einfacher kompletter Sensor

F sei eine bijektive Abbildung mit folgenden Eigenschaften :

a) F : Ra --> S

b) F(Ra) = (f · ƒ)(Ra) = f(ƒ(Ra)) = S <==> F = f · ƒ

c) F(ra) = s

F heißt die Übertragungs-Funktion des Sensors n*


Übertragungs-Funktion

Abbildung 1.5.3 - Übertragungs-Funktion F eines Sensors<


1.5.5.4 - BETRACHTUNG: einfacher kompletter Sensor

Da Elementarsensor und Umformungseinheit Teile eines einfachen kompletten Sensors sind, ergeben sich folgende Eigenschaften für den einfachen kompletten Sensor :

1) Das registrierte äußere Reizspektrum und das Zustandsspektrum des Elementarsensors sind gleichzeitig die Spektren des einfachen kompletten Sensors.

2) Das Signalspektrum der Umformungseinheit ist gleichzeitig das Signalspektrum des einfachen kompletten Sensors.

3) Die Verzögerungszeiten von Elementarsensor und Umformungseinheit addieren sich. Die gesamte Zeit vom Auftreten des Reizes bis zur Signalabgabe heißt dann Übertragungszeit Tü = Te + Tu

Es gilt dann F(ra(t)) = s(t+Tü) = s(t+Te+Tu)


1.5.5.5 - BEZEICHNUNG: Rezeptor

 Ein einfacher kompletter Sensor heißt auch Rezeptor.


1.5.5.6 - Bemerkung

 Da Elementarsensor und Umformungseinheit Teile eines einfachen kompletten Sensors sind, gelten alle bis hierher gemachten Definitionen, Betrachtungen und Bezeichnungen auch für Rezeptoren.
Von daher werden ab jetzt nur noch die Bezeichnungen Sensor und/oder Rezeptor für einen einfachen kompletten Sensor verwendet.


1.5.5.7 - BEZEICHNUNG: analoger Rezeptor

 Ein Rezeptor mit analogem Signalspektrum heißt analoger Rezeptor.


1.5.5.8 - BEZEICHNUNG: diskreter Rezeptor

 Ein Rezeptor mit diskretem Signalspektrum heißt diskreter Rezeptor.


1.5.5.9 - BEZEICHNUNG: digitaler Rezeptor

 Ein Rezeptor mit einem digitalem Signalspektrum heißt digitaler Rezeptor.


Analog zur bisherigen Vorgehensweise läßt sich der Signalraum für eine Menge von Sensoren und damit auch für beliebige Sensorensysteme beschreiben.


1.5.6 - DEFINITION: Signalraum S(N*) für ein Sensorsystem N*

 N* sei eine endliche Menge Sensoren mit n* Element von N*

<Rn>_>N* sei der n-dimensionale Reizraum der Sensormenge N*

Die (Vereinigungs)Menge aller Signalspektren S der Sensoren von N* heißt der Signalraum S(N*) der Sensormenge N*
Signalraum


1.5.6.1 - SCHREIBWEISE

 S(N*) <==> N*_><S> <==> die (Signal)Menge S von N* emittiert

S(N*)<==> N*_><S1...Sn> <==> S1 bis Sn von N* emittiert


1.5.6.2 - BEZEICHNUNG : n-dimensionaler Signalraum

 N*_><S1...Sn> = N*_><Sn> heißt n-dimensionaler Signalraum der Sensoren von N*


1.5.6.3 - Beispiele

 1) Für Steuerungen von Maschinen bzw. Fabrikationsanlagen werden in der Regel Mikrocomputer- oder SPS-Systeme verwendet. Diese verfügen über n Eingänge. An jedem Eingang ist in der Regel jeweils ein digitaler Sensor angeschlossen sind. Der Signalraum einer Maschinensteuerung ist daher ein n-dimensionaler Signalraum.

2) Wenn man in einem Computersystem Tastatur und/oder Maus als Sensoren betrachtet, so besteht dort der Signalraum aus einer Menge 8 Bit langer Worte, wobei der Signalraum aber 1-dimensional ist.

3) Bei Organismen, die ein höheres Nervensystem mit Zentralverarbeitung entwickelt haben, findet man als Signalraum eine Menge von chemo-elektrischen Impulsen bzw. Impulsfolgen, die pro Zeiteinheit abgegeben werden.

4) Alle das Auge verlassende Informationen werden durch die Sehnerven übertragen. Jeder Sehnerv verfügt über etwa 1 Millionen Fasern. Dann ist der gesamte Signalraum der optischen Erfassung 2 Millionen-dimensional, wobei die einzelnen Signalspektren aus einer Menge chemo-elektrischer Impulse besteht.

 

1.5.7 - ZWISCHENBILANZ

 Sensoren bilden die Schnittstelle (Interface) zwischen Innen und Aussen, da ja äußere Reize in innere Zustände umgesetzt werden, bzw. die inneren Zustände Reaktionen auf die äußeren Signale sind.

Sensor

Abbildung 1.5.4 - Abbildungsschema für einen Sensor


Es gibt zwar eine Abbildung von den äußeren Reizen auf die Sensorzustände, mit f(ra) = z_ñ
Reizmenge Ra und Zustandsspektrum Z_ñ sind aber nicht identisch

Es existiert also keine direkte Wahrnehmung des Äußeren. Sensor-Zustände sind daher lediglich erstes Abbild der Außenwelt.

Umgekehrt gilt aber auch, das nur das wahrnehmbar bzw. erfassbar ist, für das es auch einen Elementar-Sensor gibt, der dieses registrieren kann.
Oder kurz und bündig : Wo kein Sensor ist, da ist auch keine Wahrnehmung.

Und da wo Sensoren vorhanden sind, registrieren sie ja nur bestimmte Reize eben jene die sich in den inneren Zuständen des Sensors wiederspiegeln.
Aus der Menge der äußeren Daten wird also lediglich eine (echte) Teilmenge als äußere Reize registriert.

Sensoren wirken wie Selektionsfenster in der Wahrnehmung.

Schon an dieser Stelle läßt sich daher sagen : Das was wahrgenommen wird kann allerhöchstens nur ein Teil der Wirklichkeit sein.

Weiterhin kommt noch hinzu, das die inneren Sensorzustände noch in Signale transformiert werden. Und erst diese Sensorsignale werden ja ausgewertet.

Sensoren bzw. Rezeptoren markieren daher den Anfang der Wahrnehmungsstrecke.

 

zur vorherigen Seite zurück home weiter zur nächsten Seite

 

Der Autor - Klaus Piontzik