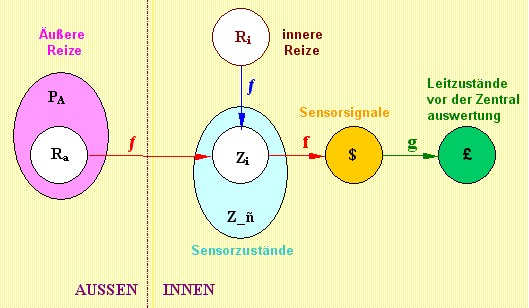
Wenn wir des Nachts im Freien stehen und uns die Sterne anschauen, so wissen wir heute, das das was wir dort sehen, keine Gegenwart darstellt. Das Licht der Sterne braucht zum Teil Jahre bzw. (je nach Entfernung) hunderte oder auch abertausende von Jahren um uns zu erreichen. Selbst das (von der Sonne stammende) und reflektierte Licht des Mondes benötigt etwa eine Sekunde, um vom Mond zur Erde zu gelangen. Und tagsüber wenn wir die Sonne sehen, ist dieses Bild etwa 8 Minuten alt. Wir nehmen also etwas Vergangenes wahr. In der Regel sind wir uns aber nicht bewusst, das genau dieser Vorgang sich auch ständig in unseren Nervenbahnen wiederholt Jeder physikalische Vorgang, d.h jeder Energietransport bzw. jeder energiebehaftete Informationstransport in diesem Universum benötigt Zeit. So werden die abgegebenen Sensordaten auch nicht direkt im Gehirn empfangen, sondern benötigen eine gewisse Zeitspanne, bis sie ihr Ziel erreichen. Es handelt sich hier um eine Spanne von maximal ein paar hunderstel Sekunden, die wir noch nicht einmal bemerken. Erst wenn wir mit Prozessen konfrontiert werden, die wesentlich schneller ablaufen, erleben wir auch die Grenzen, z.B. bei Verkehrsunfällen. Wir nennen dies dann Schrecksekunde. Es handelt sich hier um die Erkennungszeit, die mithin ein Teil der Reaktionszeit ausmacht. Regeltechnisch gesehen handelt es sich hier ja um die Totzeit eines Systems, d.h. um die Zeit in der das System bzgl. eines äußeren Reizes nicht handeln kann. Um Reaktionen schneller zu gestalten, hat die Natur Reflexe geschaffen. Dies betrifft jedoch nur bestimmte Sensorsignale. Alles was zur zentralen Auswertung wichtig ist, muß zum Gehirn gesandt werden. Hinzu kommt das durch die sequentielle Weiterleitung der elektrochemischen Impulsfolgen unsere Nervenbahnen nur über eine gewisse Kanalkapazität verfügen. Werden hier die Grenzen überschritten, so bezeichnen wir das als Reizüberflutung. Aufgrund der Modelle der Verkehrstheorie (einem Teilgebiet der Informatik) läßt sich folgendes sagen: Reizweiterleitung ist ein temporaler Prozeß, der mit einer bestimmten maximalen Übertragungskapazität behaftet ist. D.h. die inneren Leitzustände, die schließlich unser Gehirn erreichen sind gegenüber den (von den Sensoren) ausgesandten Daten zeitlich verzögert. Genau genommen bilden die Leitzustände die von den Sensoren der Wahrnehmungsorgane kommen nur eine Teilmenge der vor dem Gehirn auftretenden gesamten Menge von Leitzuständen. Es existieren da ja noch die Informationen über den inneren Organismuszustand, d.h. über Organe, Gliedmaßen, Körperzustand. Es lassen sich so zwei Arten von Sensoren bestimmen, die peripheren Sensoren die für die äußere Wahrnehmung zuständig sind und die inneren Sensoren, die zur Körper-Wahrnehmung gehören. Dies gilt für biologische wie für technische Systeme DEFINITION: periphere und innere SensorenDie Menge der Sensoren (in einem Regelkreis-System), die zur Erfassung äußerer Reize dienen, heiße Menge Np der peripheren Sensoren. Menge der äußeren Reize : RaDie Menge der Sensoren, die zur Erfassung des Trägersystems (Organismus,Körper) dienen, heiße Menge Ni der inneren Sensoren. Menge der Körperzustände (innere Reize) : Ri 1.6.1 - DEFINITION: periphere und innere SignalräumeNp ist die Menge der peripheren Sensoren und S(Np) sei der zugehörige periphere SignalraumNi ist die Menge der inneren Sensoren und S(Ni) sei der zugehörige innere Signalraum $ = S(Np)
U S(Ni) sei der gesamte
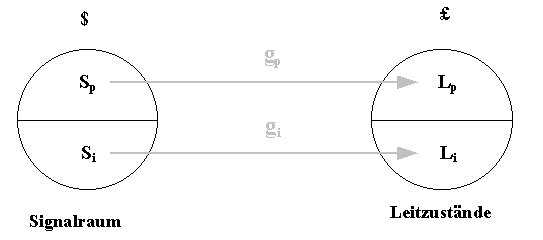
Signalraum eines Systems 1.6.2 - DEFINITION: periphere und innere LeitzuständeLp sei die Menge der Leitzustände die von den peripheren Sensoren stammenLp heiße Menge der peripheren Leitzustände Li sei die Menge der Leitzustände die von den inneren Sensoren stammen Li heiße Menge der inneren Leitzustände £ sei die Gesamtmenge der Leitzustände die am Gehirn anliegen mit £ = Lp U Li 1.6.3 - BemerkungDa die Signalweiterleitung in der Regel über einzelne Nervenfasern erfolgt, sind periphere und innere Signalmengen in der Regel zueinander disjunkt, desgleichen sind die entsprechenden Leitzustandsmengen zueinander disjunkt.Da die Menge der Leitzustände ? aus dem Signalraum $ durch Transformation.und Verzögerung entsteht, und beide dadurch auch eindeutig zuzuordnen sind, läßt sich auch hier der Begriff der Abbildung anwenden. Jedem Sensorsignal wird der entsprechende Leitwert zugeordnet. 1.6.4 - DEFINITION: Weiterleitungs-Funktion g$ sei der Signalraum der peripheren und inneren Sensoren mit s ist Element von $ und s = s(t)s(t) ist das zum Zeitpunkt t auftretende Sensorsignal £ sei die Gesamtmenge der Leitzustände die von den Sensoren stammen und l ist Element von £ Die Signallaufzeit heiße Tg Dann sei g eine bijektive Abbildung mit g : $-->£ und g(s) = l bzw. g(s(t)) = l(t+ Tg) g heißt allgemeine Weiterleitungs-Funktion
Abbildung 1.6.1 - Weiterleitungs-Funktion g 1.6.5 - DEFINITION: periphere und innere Weiterleitungs-FunktionAus der Disjunktivätät der inneren und peripheren Signalräume, und der Disjunktivität der inneren und peripheren Leitzustandsmengen folgt, das sich die Weiterleitungsfunktion zerlegen läßt, und zwar in die periphere Weiterleitungsfunktion gp und in die innere Weiterleitungsfunktion gi.Es gilt dann : gp(Sp) = Lp und gi(Si) = Li mit gp U gi = g
Abbildung 1.6.2 - periphere Weiterleitungs-Funktion gp und innere Weiterleitungsfunktion gi 1.6.6 - BemerkungSowohl die periphere als auch die innere Weiterleitungsfunktion lassen sich weiter differenzieren.Da bei den Sinnesorganen sowohl Sensoren wie auch Leiterbahnen zueinander disjunkt sind, (z.B. wie bei Hören und Sehen) kann die periphere Weiterleitungsfunktion noch zerlegt werden in die einzelnen peripheren Sinnes-Weiterleitungsfunktionen. z.B. für Nervensysteme, für Organe bzw. Organesysteme oder dem Aktorensystem. Die bislang betrachtete Wahrnehmunsstrecke lässt sich dann folgendermaßen darstellen:
Abbildung 1.6.3 - Bisher analysierte Wahrnehmungsstrecke |