Sonnenring am Bodensee

Sonnenring am Bodensee

50 sakrale Stätten in einer Spiralanordnung

Copyright © Klaus Piontzik

 

1.3 - Spiralansatz

1.3.1 - Funktionsbildung

Da die Nullachse bei 226 Grad festliegt lassen sich die Winkelangaben (von Heiden aus gesehen) umrechnen in einen laufenden Winkel, wenn man die Werte nach wachsendem Abstand (von Heiden) sortiert.

Die erste Spalte in der Tabelle gibt die Anzahl der Spiralumdrehungen wieder. Die Spalte Spiralwinkel ergibt sich aus den Spiralumdrehungen und dem Winkel von Heiden aus. Der Umlaufende Winkel ergibt sich aus dem Spiralwinkel bezogen auf die Nullachse.

 

Der Abstand (von Heiden aus) lässt sich mathematisch so als Funktion des Umlaufwinkels darstellen.

 

Umdrehung Nr. Winkel Spiralwinkel Umlaufender
Winkel		 Abstand
           
0 1 275,55 275,55 50,24 142,3
0 3 290,38 290,38 65,07 587,5
0 4 45,5 45,5 180,19 1653,40
0 5 111,16 111,16 245,85 2439,80
0 6 136,36 136,36 271,05 1971,30
0 7 223,33 223,33 358,02 2133,00
0 8 280,63 280,63 415,32 1956,60
0 9 294,78 294,78 429,47 1798,00
0 10 306,9 306,9 441,59 2050,40
0 11 308,98 308,98 443,67 2005,60
1 12 8 368 502,69 2284,50
1 13 49,6 409,6 544,29 3397,40
1 14 112,9 472,9 607,59 4293,20
  15        
1 16 124,4 484,4 618,69 4402,90
1 17 132,52 492,52 627,21 4120,30
1 51 150,58 510,58 645,27 2961,50
1 18 180,42 540,42 675,11 3909,60
1 19 226,5 586,5 721,19 4803,20
1 21 243,62 603,62 738,31 4449,00
1 22 266,12 626,12 760,81 4780,00
  23        
1 24 291,38 651,38 786,07 4297,40
1 28 315 675 809,69 4287,80
1 25 315,35 675,35 810,04 4454,80
1 26 315,5 675,5 810,19 4587,50
1 27 321,25 681,25 815,94 4584,70
2 30 8,27 728,27 862,96 3886,60
2 29 9,02 729,02 863,89 3604,60
2 31 39,27 759,27 893,96 3933,10
2 33 56,85 776,85 911,54 4727,60
2 32 61,23 781,23 915,92 4757,50
2 34 64,13 784,13 918,82 5347,20
2 35 83,1 803,1 937,79 5299,90
2 36 91,85 811,85 946,54 5854,80
2 37 101,72 821 956,754 5738,20
2 39 111,47 831,47 966,16 6131,30
2 38 112,12 832,12 966,81 6045,30
2 40 128,03 848,03 982,72 6823,80
2 41 128,7 848,7 983,39 6714,00
2 42 143,82 863,82 998,51 6275,20
2 43 146,7 866,7 1001,39 6242,70
2 45 157,33 877,33 1012,02 6190,40
2 44 157,58 877,58 1012,27 6432,00
2 46 166,52 886,52 1021,21 6439,20
2 49 175,82 895,82 1030,51 7688,80
2 48 176,03 896,03 1030,72 7390,70
2 47 176,23 896,23 1030,92 7493,60
  50        
2 52 198,32 918,32 1053,01 6532,50
2 20 232 952 1086,69 6666,30
2 53 243,4 963,4 1098,09 7826,10
2 54 284,23 1004,23 1138,92 7822,10
2 55 286,83 1006,83 1141,52 8821,80
2 57 301 1021 1154,69 6118,30
2 56 302,93 1022,93 1157,62 7323,00
2 58 316,95 1036,95 1171,64 7163,50
3 59 77,47 1157,47 1292,16 8068,30
3 61 85,22 1165,22 1299,91 7559,30
3 60 85,92 1165,92 1300,61 7272,40
3 62 124,03 1204,03 1338,72 8315,50
3 63 149,05 1229,05 1363,74 10335,10
3 64 182,65 1262,65 1397,34 9970,50
3 65 198 1278 1412,69 9761,60
3 66 213,63 1293,63 1428,32 10924,10
3 67 226,37 1306,37 1441,06 11592,60
3 69 240,88 1320,88 1455,57 11.850,20
3 68 241,57 1321,57 1456,26 12.689,40
3 70 254,32 1324,32 1459,01 12087,50
3 71 259,33 1329,33 1464,02 12022,80
3 72 279,62 1359,62 1494,31 12223,20
3 73 298,02 1378,02 1512,71 11676,20
3 74 317,02 1397,02 1531,71 10659,50

 

Diese Abstandstabelle wird bei allen Spiralansätzen noch weiter benutzt und ausgewertet. Und dort wird sie einfach als Abstandstabelle bezeichnet.

 

 

1.3.2 - Funktionale Darstellung

Die Verteilung für die ersten 50 Orte aus der Tabelle sieht graphisch dann so aus:
 
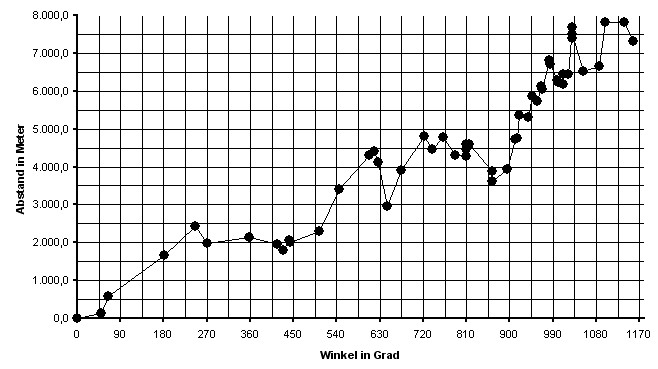Diagramm für 50 Orte
 
Als diese Studie zur Spirale 2007 entstand war die Betrachtung der Spiralanlage auf 50 Orte beschränkt. Im Laufe der Untersuchung erwies es sich jedoch als sinnvol die Anzahl der Orte auszudehnen und zwar auf 74.
 
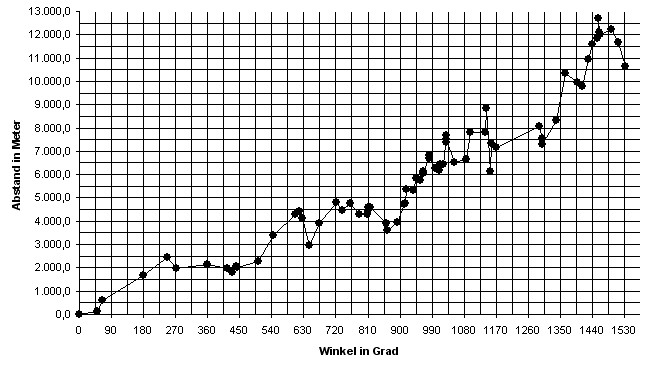Diagramm 74 Orte

 

 

1.3.3 - Mathematischer Ansatz

Bei (den meisten) Spiralen ist der Abstand vom Nullpunkt stets eine Funktion des umlaufenden Drehwinkels. Es existieren mehrere Arten von Spiralen. Die wichtigsten (die mathematisch durch eine Gleichung dargestellt werden können) sind:

1) Gleichung für eine (lineare) archimedische Spirale: R(φ) = A·φ

2) Gleichung für eine quadratische Spirale: R(φ) = A·φ2 + B·φ + C

3) Gleichung für eine logarithmische (exponentielle)Spirale: R(·φ) = A·eφ

R = Abstand vom Nullpunkt

A,B,C = Konstanten

φ = Drehwinkel

Bemerkung:
Es existieren noch weitere Spiralformen, die zum Teil aber nicht durch eine einzige Gleichung darstellbar sind. Wie z.B. eine Spirale die aus einzelnen Kreisbögen zusammen gesetzt ist.

 

zum Anfang der Seite

zur vorherigen Seite zurück home weiter zur nächsten Seite

 

Sonnenring am Bodensee

bei Amazon kaufen

 120 Seiten, davon 76 in Farbe
110 Bilder

Herstellung und Verlag:
Books on Demand GmbH, Norderstedt

ISBN 9783756215683

Ladenpreis: 17 Euro

zur PiMath Homepage