Copyright © Klaus Piontzik
| 1.0.0 | Einleitung - π als Näherungswert | ||
| 1.1.0 | Ägypten | 1850/1650 v.Chr. | |
| 1.2.0 | Babylonien | 1900 - 1600 v.Chr. | |
| 1.3.0 | Die Griechen | 400 - 300 v.Chr. | |
| 1.3.1 | Archimedes | 287 - 212 v.Chr. | |
| 1.3.2 | Apollonius von Perge | 262 - 190 v.Chr. | |
| 1.3.3 | Heron von Alexandria | 10-75 n.Chr. | |
| 1.3.4 | Claudius Ptolemäus | 85-165 n.Chr. | |
| 1.4.0 | China | 250/430-501 n.Chr. | |
| 1.5.0 | Indien | 500 v.Chr./500 n.Chr | |
| 1.6.0 | Verfeinerte Näherungen | 1540-1600 | |
| 1.6.1 | Adriaen Metius, Valentius Otho | 1573 | |
| 1.6.2 | Ludolph von Ceulen | 1540-1610 | |
| 1.6.3 | Jacob Marcelis | 1700 | |
| 1.7.0 | Reihenentwicklungen | 1640 - 1780 | |
| 1.7.1 | π als Symbol | ||
| 1.8.0 | Lambert und die Irrtionalität von π | 1761 | |
| 1.8.1 | Lindemann und π als transzendente Zahl | 1882 | |
| 1.9.0 | Näherungswerte für π in Bruchdarstellung | ||
| 1.9.1 | Die geometrisch günstigste Näherung | ||
| Das
Verhältnis von Kreisumfang zu Kreisdurchmesser, das wir
heute mit der Zahl π ausdrücken, war
der 17. Buchstabe des ursprünglichen und ist der 16.
Buchstabe des klassischen griechischen Alphabetes. Der griechische Buchstaben ’π’ (p) zur Bezeichnung der Verhältniszahl des Kreisumfangs zum Kreisdurchmesser soll sich ableiten aus dem griechischen Wort perijeria (periphereia) = Kreis(umfang), Umkreis, Umfangslinie oder auch von perimetros, in deutsch Umfang. Über die Eigenschaften und über die Entwicklung der Zahl π ist, im Laufe der Zeit, schon viel geschrieben, gerechnet und gerätselt worden. Hier geht es allerdings nicht um irgendwelche Mysteria dieser Zahl, sondern darum geeignete Näherungswerte zu finden, die in der geometrischen Praxis, mit genügender Genauigkeit, umsetzbar sind. Daher erfolgt, in diesem
Kapitel, lediglich eine kleine Übersicht zur
geschichtlichen Entwicklung bzw. Entdeckung und
Eingrenzung der Zahl π. Unter besonderer
Berücksichtigung von Bruchdarstellungen für π,
im Hinblick auf spätere geometrische Verwendbarkeit. |
| Der wohl älteste offiziell überlieferte Wert für π stammt von den Ägyptern. Etwa um 1850 v.Chr. enstand das Moskauer Papyrus Man fand die Näherung: |
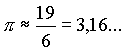 |
| Das Papyrus Rhind , dass auf etwa 1650 v.Chr. datiert wird, enthält mathematische Aufgaben in Textform, die vom Schreiber Ahmes stammen. Es gibt diesen Wert an: |
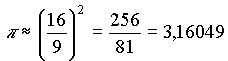 |
| Dieses Dokument befindet sich heute im Britischen Museum in London. |
| Es könnte aber auch schon vor der Abfassung des Papyrus Rhind bessere Näherungswerte gegeben haben: POSAMENTIER (The Mathematics Teacher v. 77(1); S.52,47) führt das Buch "La Science Mystérieuse des Pharaons" von Abbé Moreux (Paris 1923) an, wo auf den Seiten 28-29 eine vermutete Näherung von 3,14159294 angegeben wird. (zitiert nach Mäder 1989, S.55) |
| Etwa zur selben Zeit wie in Ägypten (1900-1600 v.Chr.) gab es auch schon in Babylonien erste Näherungen für π. Der Wert 3 wurde als solche Näherung benutzt. Keilschrifttexte, die 1936 in Susa entdeckt wurden, geben für π diesen Wert an: |
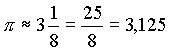 |
| Die
Quadratur des Kreises war eines der Lieblingsthemen der
alten Griechen. Die Aufgabe war, zu einem gegebenen
Kreis, nur mit Hilfe von Lineal und Zirkel, ein umfang
bzw. flächengleiches Quadrat zu konstruieren. Dieses
sollte in einer begrenzten Anzahl von Schritten
bewältigt werden. Aus noch zu ersehenden Gründen ist
dies geometrisch exakt aber unmöglich. Antiphon (430 v.Chr.) war der Meinung, daß
die Quadratur des Kreises und damit die exakte Bestimmung
von p möglich sein müsse, weil sich jedes Polygon in
ein Quadrat verwandeln läßt. Bryson
aus Herakleia ging noch einen
Schritt weiter und berechnete die Fläche von zwei
Vielecken – eines das den Kreis von innen begrenzte
und eines zweiten das den Kreis von außen umschloss. Die
Fläche des Kreises, so folgerte Bryson, müsse zwischen
den Flächen der beiden Vielecke liegen. Euklid von Alexandria (325-265 v. Chr.) gelang der Beweis, daß 3 < π < 4 gilt. Doch erst Archimedes konnte rund 100 Jahre später diese Ungleichung verfeinern. |
| Auf Archimedes von Syrakus (287 - 212 v.Chr.) geht folgende Ungleichung zurück, die er durch die Konstruktion eines 96-Ecks gewann: |
|
| Auf Apollonius von Perge (262 - 190 v.Chr.), einem jüngeren Kollegen von Archimedes, geht folgender Wert zurück: |
| Nach Angaben des Mathematikers Heron von Alexandria (10-75 n. Chr.) soll Archimedes sogar eine noch bessere Abschätzung für π gefunden haben. Es ist aber nicht vollständig geklärt, ob dieser Ausdruck wirklich von ihm stammt. Seine Angabe lautet: |
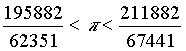 |
| Der griechische Astronom Claudius Ptolemäus (85-165 n.Chr. in Ägypten) nützte die Vorarbeit des Archimedes und setzte dessen Methode bis zum 720-Eck fort. Damit erreichte er für π die Näherung : |
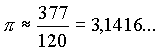 |
| Von Wang Fan um 250 n.Chr. stammt die Näherung: |
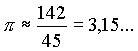 |
| Der Astronom Tsu Chu'ung-Chi (430-501 n.Chr.) und sein Sohn Tsu Keng-Chi fanden diese Näherung: |
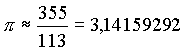 |
| Tsu
Ch’ung Chi (Zu Chong Zhi) wurde als Mathematiker und
Astronom bekannt und war etwa 800 Jahre lang der
Weltrekordhalter in der Präzision der Darstellung von
π. Die Wissenschaftshistoriker wissen nicht sehr viel über ihn. Insbesondere ist rätselhaft, wie Tsu seine erstaunliche Approximation der Kreiszahl π berechnet hat. Über den Ursprung dieses einfachen Bruches gibt es nur Vermutungen, die besagen, daß Tsu einfach die bekannten Brüche von Ptolemäus und Archimedes verwendet hat. Indem er die Differenz der Zähler und Nenner bildete: |
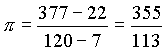 |
| Um 500 v.Chr. waren für π Näherungen in Gebrauch, wie zum Beispiel: |
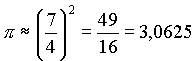 |
| Noch öfter findet man einen Wert, der auch als Hinduwert bezeichnet wird: |
Der indische Mathematiker Brahmagupta (geboren 598 n.Chr.) fand 640 n.Chr. ebenfalls diesen Wert, indem er die Summe der Seitenlängen von 12-, 24-, 48- und 96-seitigen Polygonen berechnete. Um 499-510 n.Chr. gab Aryabhatiya (476-550) für π eine Näherung an, die auch im Paulisha Siddhanta erwähnt wird: |
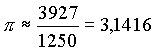 |
| Im Mittelalter wurden, in Europa, die Verfahren zur Berechnung von π erheblich verfeinert. Tycho de Brahe (1546-1601), ein dänischer Astronom, nahm für π den Wert: |
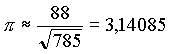 |
| Der
französische Mathematiker und Rechtsgelehrte Francois Viete (1540-1603) drang 1579, in
Fortsetzung der archimedischen Methode, bis zum
393216-Eck vor. Er erhielt eine Ungleichung, die den Wert
für π bis auf 9 Dezimalstellen angab. Viete, (lateinisch Vieta) der "Vater" der modernen Algebra, stellte erstmals eine geschlossene Formel für π vor, die sich aus einem unendlichen Produkt ableiten läßt. |
| Dieses Produkt fand Leonard Euler dann etwa 150 Jahre später. Die Konvergenz dieses Ausdrucks konnte aber erst F. Rudio im Jahre 1891 beweisen. |
| Mehr als 1000 Jahre nach Tsu Ch'ung-Chi entdeckte Adriaan Metius dieselbe Näherung 355/113, als er das arithmetische Mittel von Zähler und Nenner der beiden Näherungen 377/120 und 333/106, die auf Berechnungen seines Vaters beruhten, bildete. Beachtenswert ist hier, das durch den relativ einfachen Bruch 333/106 insgesamt 4 Dezimalstellen von π anfallen: |
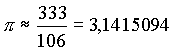 |
| Zu erwähnen wäre noch Valentinus Otho , durch den im Jahre 1573 die Näherung 355/113 bekannt wurde. |
| Um einen Eindruck von der Faszination dieser Zahl in vergangenen Jahren zu vermitteln, dient der niederländische Mathematiker Ludolf von Ceulen (1539-1610). Er errechnete π auf 35 Stellen genau. Hier sein Wert, der auch heute noch gültig ist: |
| π = 3,14159265358979323846264338327950288... |
| Ludolph
van Ceulen widmete einen grossen Teil seiner Arbeit und
seines Lebens der Berechnung der Zahl π. 1596 errechnete
er 20 richtige Stellen und kurz vor seinem Tod weitere
15. Dabei diente ihm die Archimedische Methode als
Grundlage. Er benutzte ein- und umschriebene Polygone mit
262 Seiten. Die letzten drei der von ihm
berechneten Ziffern wurden in seinen Grabstein
eingemeisselt. Daher wird π auch manchmal als Ludolphsche Zahl bezeichnet. |
| Um 1700 herum war Jacob Marcelis der Meinung, daß es ihm gelungen sei, den Kreis zu quadrieren, und damit den exakten Wert für π zu bestimmen. Diesen gab er wie folgt an: |
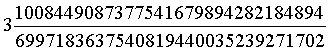 |
| Von Gottfried Wilhelm Leibniz (1646-1716), einem deutschen Philosoph und Universalgelehrten, stammt die nachfolgende Reihe für π, die er bei der Untersuchung des Konvergenzverhaltens unendlicher Reihen 1673 fand. |
| Die
einfache, aber nur sehr langsam konvergierende Formel
läßt sich mit Hilfe der Potenzreihe des Arcustangens
ableiten. Leibniz fand unabhängig von Newton die
Differential- und Integralrechnung Durch die Ausarbeitung der
Analysis, von dem englischen Physiker, Mathematiker und
Astronom Isaac
Newton (1642 -
1727) und dem Schweizer Mathematiker Leonhard Euler (1707-1783), konnten bessere
Näherungswerte von π gefunden werden. |
| Der
griechische Buchstaben ’π’ (p) zur Bezeichnung
der Verhältniszahl des Kreisumfangs zum Kreisdurchmesser
soll sich ableiten aus dem griechischen Wort perijeria
(periphereia) = Kreis(umfang), Umkreis, Umfangslinie oder
auch von perimetros, dt. Umfang. Der griechische Buchstabe π wurde als Abkürzung für "Peripherie" von englischen Mathematikern benutzt, genannt werden hier William Oughtred (1667) und Issac Barrow (1630-1677). Weiterhin William Jones (1675-1749) mit seinem Werk „Synopsis palmariorum matheseos“. Doch ihre Beispiele blieben ohne Nachahmung. Aufgegriffen wurde der Buchstabe später von Leonhard Euler in seiner Abhandlung „Variae observationes circa series infinitas“. Euler verwendet zunächst p bis 1735, ab 1738 dann π. Danach etablierte sich der griechische Buchstabe auch bei anderen Mathematikern als Symbol für die Kreiskonstante und setzte sich so dann überall durch. Euler fand u.a. die Beziehung eiπ + 1 = 0 , die eine Voraussetzung für Lindemanns Beweis der Transzendenz von π ist. |
| Johann Heinrich Lambert
(1728-1777), deutscher
Mathematiker, Physiker, Astronom und Philosoph, gelang es
im Jahre 1761, die Irrationalität von π zu beweisen. Irrationalität einer Zahl besagt, das sie nicht als Bruch zweier ganzen Zahlen darstellbar ist. Lambert nähert sich der Kreiszahl durch eine Folge von Brüchen. Zuerst zeigte er, daß tan
x nicht rational sein kann, wenn Mit Hilfe von Kettenbrüchen konnte er auch die besten Näherungen in Form von Brüchen berechnen. Dazu zählt beispielsweise: |
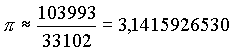 |
| Der
deutsche Mathematiker Ferdinand von Lindemann
(1852-1939) bewies dann im
Jahre 1882, das π eine transzendente
Zahl ist, d.h.
unter anderem: π ist unendlich und unperiodisch. Unendlichkeit und Unperiodizität langen allein allerdings nicht aus, um Transzendenz einer Zahl zu gewährleisten. Transzendenz einer Zahl bedeutet: Lösung einer Gleichung mit GANZZAHLIGEN oder RATIONALEN Koeffizienten und dabei keine algebraische Zahl zu sein. Den Beweis veröffentlichte er in dem Artikel "Über die Zahl π" in den "Mathematischen Annalen" in München. Zuerst bewies Lindemann, daß die Lösung von eiπ + 1 = 0 nicht algebraisch sein kann. Er wußte aber, daß π dieser Gleichung genügte (das hatte schon Newton bewiesen), woraus er noch weiter folgerte, daß π keine algebraische Zahl sein kann. Die Konsequenz ist, das eine Konstruktion der Zahl π durch Lineal und Zirkel, also die geometrische Quadratur des Kreises nicht exakt möglich ist. Unter der Quadratur des Kreises versteht man entweder die Umformung des Kreisumfangs in ein umfanggleiches Quadrat oder die Umwandlung der Kreisfläche in ein flächengleiches Quadrat. Zu erwähnen wäre da noch das, seit den Griechen, quasi ganze Generationen von Mathematikern vorher versucht hatten, eine Lösung der Quadratur mit Zirkel und Lineal zu erreichen. Lindemanns Beweis zeigt demzufolge auch die Aussichtslosigkeit eines solchen Unterfangens. Was andererseits bedeutet, das vorhandene geometrische Konstruktionen, die Quadratur des Kreises betreffend, als Näherungslösungen zu betrachten sind. Und bei Näherungen, das heißt bei ihrer Anwendung und Benutzung, spielt eher die Frage der Genauigkeit eine grosse Rolle. |
| Wie in der obigen historischen Betrachtung behandelt worden ist, läßt sich π durch Bruchdarstellungen annähern. Hier einige Beispiele, wie sie im Laufe der Zeit auch immer wieder von verschiedenen Autoren benutzt worden sind. Die erste abweichende Dezimalstelle ist dabei rot markiert und die Ziffernfolge wird hier abgebrochen. |
|
Tabelle - Näherungen für π in Bruchdarstellung
| Praktisch geometrisch gesehen, also aus Gründen der Konstruierbarkeit, sind quasi nur die Bruchdarstellungen deren Nenner kleiner als 1000 sind, verwendbar. Und hier fallen lediglich 4 Werte auf: |
| Tsu Chu'ung-Chi Die Darstellung von π durch 355/113 - die ersten 6 Stellen hinter dem Komma sind exakt Adriaen Metius Claudius
Ptolemäus Archimedes |
| Die angegebenen Näherungen lassen sich geometrisch nutzen bzw. umsetzen, so das eine Quadratur des Kreises, als annähernde Konstruktion, lediglich mit Zirkel und Lineal ausgeführt, also durchaus möglich ist. |
| Die am häufigsten verwendete Näherung für π ist der von Archimedes verwendete Wert 22/7 |
| Dadurch reduziert sich das Thema Quadratur des Kreises auf zwei Zahlen: die 7 und die 11. Es ergeben sich hier zwei Möglichkeiten: das 14:11 und das 11:7 Verhältnis. Aus jeder Proportion resultiert eine spezifische Quadraturkonstruktion. |
|
280
Seiten 227 Bilder, davon 55 in Farbe Herstellung und Verlag: Books on Demand GmbH, Norderstedt ISBN 9783757881207 Ladenpreis: 22 Euro |