KRITERIEN ZUR GEOMETRIEBESTIMMUNG IN LANDSCHAFTEN
Copyright © Klaus Piontzik
| Nach den Angaben von Jens
M. Möller ergeben sich folgende Orte auf der
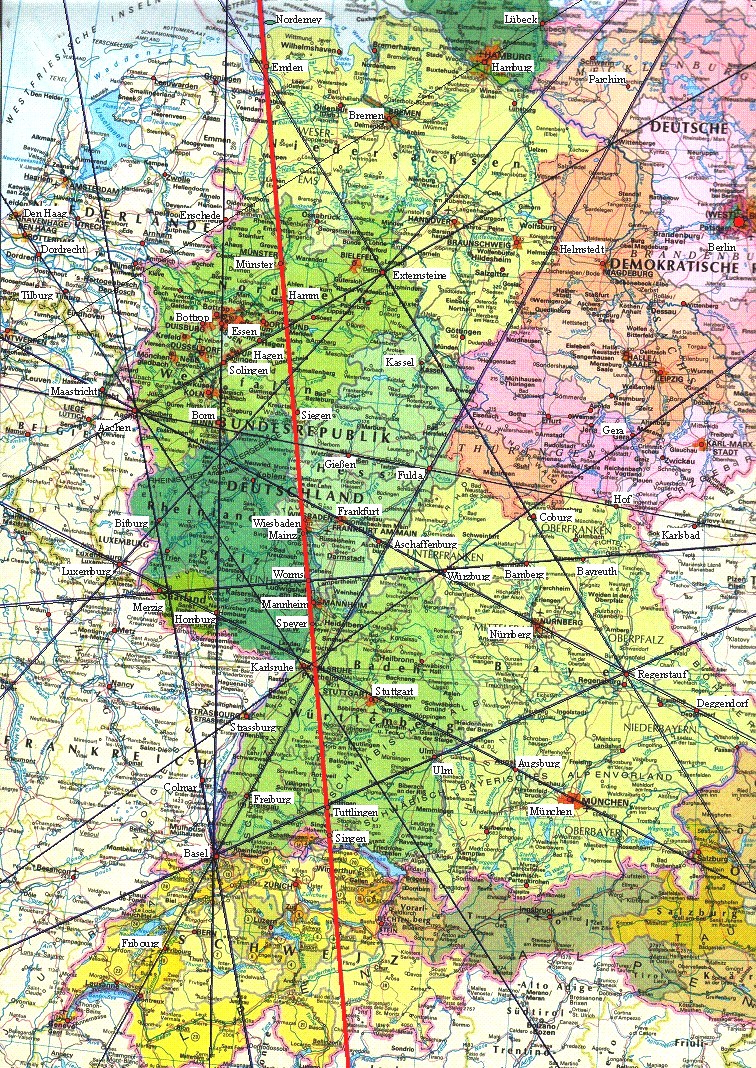
Drei-Kaiser-Dom-Linie: Norderney, Hamm, Werl, Kreuztal, Siegen, Mainz, Worms, Speyer, Karlsruhe, Berneck, Hohentwiel (Singen) Einzeichnen in eine Deutschland-Karte führt zu folgendem Resultat: |

| Aus der Karte ergeben
sich noch folgenden zusätzlichen Orte: Emden, Münster, Wiesbaden, Mannheim, Tuttlingen |
| Für alle angegebenen Orte lauten die geographischen Koordinaten: |
| Norderney Phi = 53° 42´ N geographische Breite Lambda = 07° 10´ O geographische Länge Emden Phi = 53° 22´ N geographische Breite Lambda = 07° 12´ O geographische Länge Münster Phi = 51° 58´ N geographische Breite Lambda = 07° 38´ O geographische Länge Hamm Phi = 51° 41´ N geographische Breite Lambda = 07° 48´ O geographische Länge Werl Phi = 51° 33´ N geographische Breite Lambda = 07° 55´ O geographische Länge Kreuztal Phi = 50° 58´ N geographische Breite Lambda = 07° 59´ O geographische Länge Siegen Phi = 50° 52´ N geographische Breite Lambda = 08° 02´ O geographische Länge Wiesbaden Phi = 50° 50´ N geographische Breite Lambda = 08° 14´ O geographische Länge Mainz Phi = 50° 00´ N geographische Breite Lambda = 08° 15´ O geographische Länge Worms Phi = 49° 38´ N geographische Breite Lambda = 08° 21´ O geographische Länge Mannheim Phi = 49° 29´ N geographische Breite Lambda = 08° 28´ O geographische Länge Speyer Phi = 49° 19´ N geographische Breite Lambda = 08° 26´ O geographische Länge Karlsruhe Phi = 49° 01´ N geographische Breite Lambda = 08° 24´ O geographische Länge Berneck (Altensteig) Phi = 48° 36´ N geographische Breite Lambda = 08° 37´ O geographische Länge Tuttlingen Phi = 47° 59´ N geographische Breite Lambda = 08° 49´ O geographische Länge Singen (Hohentwiel) Phi = 47° 46´ N geographische Breite Lambda = 08° 50´ O geographische Länge |
| Sind die geographischen
Koordinaten (Breite, Länge) von zwei Orten bekannt, so
kann man mit der sogenannten zweiten geodätischen
Hauptaufgabe den Abstand als auch die Richtungen
berechnen. Der Abstand X (als Winkel) der beiden Punkte zueinander ergibt sich mit:
Und der Winkel vom Ursprungsort aus gesehen lautet:
Ausgehend von einem Ursprungsort lassen sich jetzt die Winkel zu den einzelnen Orten auf der Linie berechnen. Da Worms im Schnittpunkt der Drei-Kaiser-Dom-Linie und der Siegfried-Linie liegt, ist es sinnvoll Worms als Bezugspunkt zu nehmen. |
| von Worms nach | Richtung |
| Norderney | 9,7686 NW |
| Emden | 10,4071 NW |
| Münster | 10,7089 NW |
| Hamm | 9,4405 NW |
| Werl | 8,0008 NW |
| Kreuztal | 9,8222 NW |
| Siegen | 9,6771 NW |
| Wiesbaden | 9,4441 NW |
| Mainz | 9,9422 NW |
| Worms | 0 |
| Mannheim | 26,8164 NW |
| Speyer | 9,7351 NW |
| Karlsruhe | 3,0440 NW |
| Berneck (Altensteig) | 9,6882 NW |
| Tuttlingen | 10,7273 NW |
| Singen (Hohentwiel) | 9,8798 NW |
| Lediglich die Richtungen
für Werl, Mannheim und Karlsruhe weichen von den anderen
Richtungen ab. Ebenfalls die Richtungen für Emden,
Münster und Tuttlingen. Sie werden daher zur mittleren
Richtungsfindung erstmal nicht weiter berücksichtigt. Bildet man aus den restlichen Werten den Mittelwert, so erhält man die mittlere Ausrichtung der Linie. Die mittlere Ausrichtung der Drei-Kaiser-Dom-Linie beträgt 9,7109 Grad NW bzw. 170,2891 Grad NO. |
| Nach den Kriterien zur
Geometriebestimmung muß eine Linie durch mindestens vier
Punkte gekennzeichnet sein. Zur Differenzierung nimmt man nur die Punkte die, nach den Kriterien zur Geometriebestimmung, auf bzw. an einer Linie liegen als eigentliche Linienorte. Die nebenliegenden Orte werden dann nur noch zur ergänzenden Betrachtung benötigt. |
| Nach den Kriterien zur
Geometriebestimmung heißt eine Umgebung eines beliebigen
geographischen Ortes mit einem Radius, der größer als
1000 Meter ist, Gebietsumgebung des
Ortes. Zur Behandlung der hier angegebenen Orte und ihr
Verhältnis zur Drei-Kaiser-Dom-Linie dürften
Gebietspunkte ausreichen. Die Beziehungen eines Ortes zu einer Linie nach der bisherigen Definition für Umgebungspunkte lassen sich dann einfach auf die Gebietspunkte übertragen. Berücksichtigt man das der 1000 Meter Radius eines Gebietspunktes gerade den Ortskern einer heutigen Stadt darstellt, lassen sich die Kriterien für Punkte noch etwas differenzieren |
| Beziehung zur Linie | Radius |
| genau auf | bis 500 m |
| auf | 500 bis 1000 m |
| an | 1000 bis 5000 m |
| in der Nähe | 5000 m bis 50 Km |
| Mit der gefundenen
mittleren Richtung lässt sich jetzt noch die Entfernung s
bestimmen, die ein Ort von der mittleren Linie besitzt.
Wenn X die Entfernung zwischen den zwei
Punkten ist, und delta alpha die
Richtungsdifferenz zur mittleren Richtung, dann lässt
sich der Abstand nach folgender Gleichung berechnen
Werden die Winkel in Bogenmaß benutzt, dann lässt sich annähernd der Abstand eines Ortes (in Kilometer) zur Linie berechnen:
|
| Ort | Abstand [Km] zur Linie | Beziehung zur Linie |
| Norderney | 0,462 | genau auf |
| Emden | 5,131 | in der Nähe |
| Münster | 4,602 | an |
| Hamm | 1,091 | auf |
| Werl | 6,423 | in der Nähe |
| Kreuztal | 0,292 | genau auf |
| Siegen | 0,082 | genau auf |
| Wiesbaden | 0,236 | genau auf |
| Mainz | 0,167 | genau auf |
| Mannheim | 5,494 | in der Nähe |
| Worms | 0 | genau auf |
| Speyer | 0,015 | genau auf |
| Karlsruhe | 7,970 | in der Nähe |
| Berneck | 0,046 | genau auf |
| Tuttlingen | 3,310 | an |
| Singen | 0,621 | auf |
| Norderney, Emden,
Münster, Hamm, Kreuztal, Siegen, Wiesbaden, Mainz, Worms,
Speyer, Berneck, Tuttlingen, Singen liegen auf bzw. an der Drei-Kaiser-Dom-Linie. Entlang der Linie zwischen Norderney und Singen also einer Strecke von 670 Km befinden sich alle Orte in einem Schlauch von maximal ±4,6 km links und rechts neben der Linie. Berücksichtigt man noch Orte die in der Nähe der Linie liegen, dann erweitert sich der Schlauch auf jeweils ±8 Km. Nimmt man nur die Orte die auf bzw. genau auf der Linie liegen, also Norderney, Hamm, Kreuztal, Siegen, Wiesbaden, Mainz, Worms, Speyer, Berneck und Singen so ergibt sich ein Schlauch von maximal ±1 km. |
|
252
Seiten, davon 116 in Farbe 163 Bilder Herstellung
und Verlag: ISBN 9783755742111 Ladenpreis: 24 Euro |