Das Externstein-System - Machalett und Möller

Durchschneidet man die Cheopspyramide in nord-südlicher oder ost-westlicher Richtung, so bildet der Querschnitt ein Dreieck.
In diesem Dreieck treten ganz bestimmte Winkel - und Streckenverhältnisse auf (14:11 = 4/pi), die darauf hindeuten das hier die Quadratur des Kreises bzw. eine Näherung benutzt worden ist, also die Zahl PI (bzw. eine Näherung) in die Konstruktion eingeht.

Der deutsche Mathematiker Ferdinand von Lindemann (1852-1939) bewies im Jahre 1882, das pi eine transzendente Zahl ist, d.h. unter anderem: pi ist unendlich und unperiodisch.
Die Konsequenz ist, das eine Konstruktion der Zahl pi durch Lineal und Zirkel, also die geometrische Quadratur des Kreises nicht exakt möglich ist.

Das bedeutet, dass die vorhandene geometrische Konstruktion, die Quadratur des Kreises betreffend, als Näherungslösung zu betrachten ist. (siehe pimath.de – Quadratur des Kreises)

Die Quadratur wird, in der Regel, wie im folgenden Bild dargestellt:

Die Grundseite des Dreiecks entspricht einer Quadratseite und die Höhe des Dreiecks ist gleich dem Radius des Kreises. Kreis und Quadrat bestzen dann den gleichen Umfang.

So erklärt sich, dass das Quadraturdreieck auch als Cheops-Pyramide bezeichnet wird.

Erwähnenswert ist hier noch die sogenannte Externstein-Pyramide nach Walther Machalett. Die Spitze dieses Quadraturdreiecks wird durch die Externsteine gebildet.
Die beiden anderen Ecken des Dreiecks ergeben sich durch die Orte Salvage (Atlantis – heute etwa Lanzarote, Teneriffa) und Gizeh (Cheopspyramide).

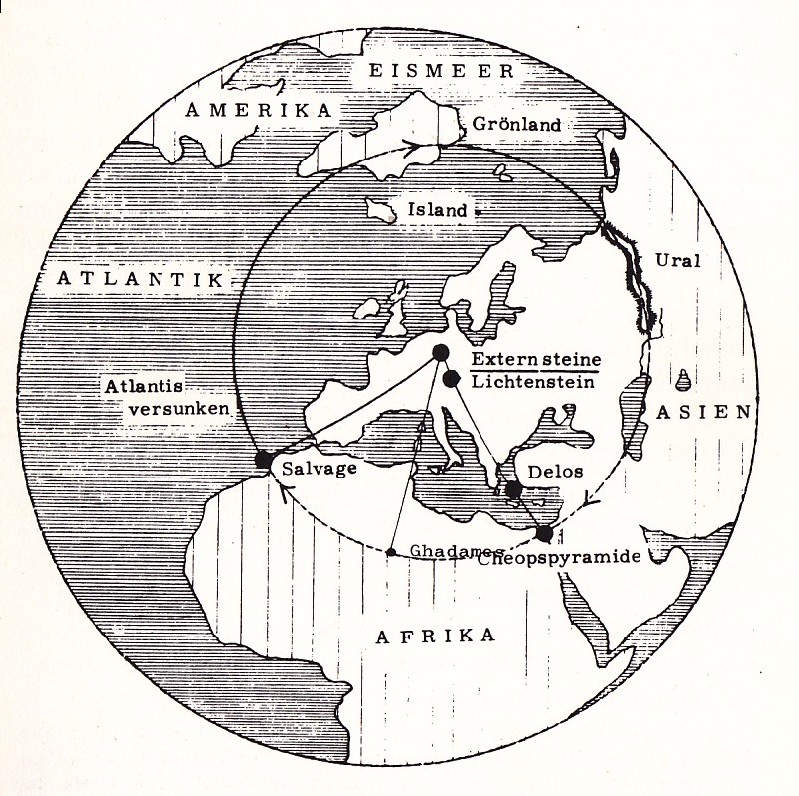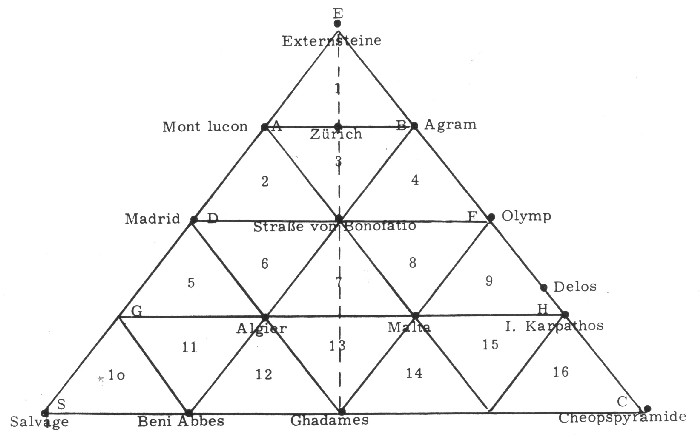Die Externsteinpyramide umfasst dabei einen Raum, in welchem die wichtigsten Mysterienorte und Kultplätze für die Entwicklung Mitteleuropas untergebracht sind.

Jens Möller gibt für die Westlinie der Externsteinpyramide folgende Orte an:

Externsteine – Bitburg – Luxemburg – Lourdes – Gibraltar - Kanarische Inseln.

Laut Jens Möller wird die Ostlinie aus folgenden Orten gebildet:

Externsteine – Kassel – Donaustauf (Walhalla) – Zagreb – Delphi - Gizeh.

Schaut man sich die Karte von Machalett genauer an, so erkennt man, dass Gizeh nicht direkt auf der Ecke liegt, sondern knapp daneben. Dies ist korrekt dargestellt, denn Gizeh liegt etwa 370 km neben der idealen Qudadratur-Linie.

Rechnet man die Orte (von Möller) und die zugehörige Ost bzw. Westlinie durch, so zeigt sich, das fast alle anderen Orte, im europäischen Raum, in etwa auf der jeweiligen Linie liegen, d.h. der Abstand zur Linie beträgt weniger als 50 km.

Auffallend an der Externsteinpyramide von Machalett ist die systematische Ausfüllung des Dreiecks mit Ost bzw. Westlinien. Heißt also, Machalett ging von einem Europa umspannenden Netz aus.Siehe dazu das Machalett-Gitter

Wenn eine größere Geometrie existiert, ist zu erwarten, dass es sie auch in einem kleineren, sprich regionalem, Rahmen gibt. Oder umgekehrt: die alten regionalen Strukturen sind dann einfach als Spiegelungen übergeordneter geomantischer Netzwerke oder Gitter zu verstehen.

Zum selben Ergebnis eines europäischen Netzes gelangt man, wenn man die Möllerschen Linien analysiert. Hier zeigt sich, dass diese Linien nicht zufällig in der Landschaft liegen, sondern Teile eines größeren Gittersystems sind.

In der obigen Karte der Linien von Möller sind folgende Linien angegeben:

Name der Linie	Orte auf der Linie

Externsteinpyramide
Meridianlinie	Externsteine, Marsberg, Marburg, Neckargmünd, Kloster Maulbronn, Haigerloch, Hohentwiel (Singen), Genua, Cagliari
Ostlinie	Externsteine (Horn), Kassel, Donaustauf (Walhalla), Zagreb, Delphi, Gizeh (Cheops-Pyramide)
Westlinie	Externsteine, Bitburg, Luxemburg (Lichtburg), Lourdes, Gibraltar, Kanadische Inseln (Atlantis)

Atlantis-Linie	Nordspitze Portugal, Chartes, Paris, Aachen, Soest, Externsteine

Drei-Kaiserdom-Linie	Norderney, Hamm, Werl, Kreuztal, Siegen, Mainz, Worms, Speyer, Karlsruhe, Berneck, Hohentwiel (Singen)

Siegfried-Linie	Rennes, Paris, Burg Esch, Worms, Lorsch, Michelstadt, Würzburg, Bayreuth, Prag

Deutschland-Linie	Aix-en-Provence, Fribourg (Belchen-Schweiz), Basel, Belchen (Freiburg), Herrenalb, Karlsruhe, Neckargmümd, Schloss Mespelbrunn, Fulda, Brocken, (Eisenach?), Helmstedt

Logen-Linie	Perth, Den Haag, Aachen, Kirn, Kalmit, Karlsruhe, Bebenhausen, Lichtenstein, Zwiefalten, Bussen, Stein (Allgäu), Nebelhorn, Leuca

Bonifacius-Linie	Southampton, Brüssel, Aachen, Fulda, Prag, Sternberk

Nornen-Linie	Donaustauf (Walhalla), Nürnberg, Würzburg, Frankfurt (Main), Königstein (Taunus), Aachen

Königs-Linie	Hochkönigsbourg (Elsaß), Königsbach/Stein, Baden-Baden, Karlsruhe, Bretten, Königsberg (Bayern), Haßfurt (Bayern), Veste Coburg, Gera, Königsberg (Preußen-Kaliningrad)

	Basel, Hochkönigsburg, Trier, Aachen

	Basel, Beuron, Zwiefalten, Ulm, Dillingen, Donaustauf (Walhalla)

	Basel, Homburg (Saar), Idar-Oberstein, Bonn, Essen, Enschede

	Luxemburg, Dahn, Bergzabern, Karlsruhe, Stuttgart, Esslingen, Augsburg, Königsbrunn, Marquartstein

	Enschede, Bremen, Hamburg, Lübeck

bei Amazon kaufen

252 Seiten, davon 116 in Farbe
163 Bilder

Herstellung und Verlag:
Books on Demand GmbH, Norderstedt

ISBN 9783755742111

Ladenpreis: 24 Euro

Die Quadratur des Kreises

Die Externstein-Pyramide von Walther Machalett

Die Linien von Jens M. Möller