ZUR ZAHL Pi - Altertum

1.1.0	Einleitung - Pi als Näherungswert
1.1.1	Ägypten	1850/1650 v.Chr.
1.1.2	Babylonien	1900 -1600 v.Chr.
1.1.3	Bibel und Talmud	550 v. Chr.
1.1.4	Die Griechen und die Quadratur des Kreises	400 - 300 v.Chr.
1.1.5	Archimedes	287 - 212 v.Chr.
1.1.6	Heron von Alexandria	10 - 75 n.Chr.
1.1.7	Apollonius von Perge	262 - 190 v.Chr.
1.1.8	Claudius Ptolemäus	85 -165 n.Chr.
1.1.9	Karpos von Antiochia	100 - 180 n.Vhr.
1.1.10	China	250/430 - 501 n.Chr.
1.1.11	Indien	500 v.Chr./500 n.Chr

1.1.0

Einleitung - π als Näherungswert

Das Verhältnis von Kreisumfang zu Kreisdurchmesser, das wir heute mit der Zahl π ausdrücken, war der 17. Buchstabe des ursprünglichen und ist der 16. Buchstabe des klassischen griechischen Alphabetes.

Der griechische Buchstabe ’π’ (p) zur Bezeichnung der Verhältniszahl des Kreisumfangs zum Kreisdurchmesser soll sich ableiten aus dem griechischen Wort perijeria (periphereia) = Kreis(umfang), Umkreis, Umfangslinie oder auch von perimetros = Umfang.

Der griechische Buchstabe π wurde als Abkürzung für "Peripherie" von englischen Mathematikern benutzt, genannt werden hier Oughtred (1667) und Issac Barrow (1630-1677) sowie William Jones (1675-1749). Doch ihre Beispiele blieben ohne Nachahmung.
Aufgegriffen wurde der Buchstabe später von Leonhard Euler etwa ab 1738. Danach etablierte sich der griechische Buchstabe auch bei anderen Mathematikern als Symbol für die Kreiskonstante und setzte sich so dann überall durch.

Über die Eigenschaften und über die Entwicklung der Zahl π ist, im Laufe der Zeit, schon viel geschrieben, gerechnet und gerätselt worden. Hier geht es allerdings nicht um irgendwelche Mysteria dieser Zahl, sondern darum eine Übersicht zur geschichtlichen Entwicklung und Entdeckung sowie Eingrenzung bzw. Approximation der Zahl π.

Abgesehen von einigen einfachen Texten (wie der Berechnung einer Quadratfläche) an der Wänden von Gräbern, sind die einzigen dokumentarischen Überlieferungen über den Stand der ägyptischen Rechenkunst hauptsächlich auf den Papyri Rhind, Kahûn, Moskau und Berlin erhalten geblieben. Der wohl älteste dokumentarisch überlieferte Wert für π stammt von den Ägyptern.

Moskauer Papyrus

Etwa um 1850 v.Chr. entstand das Moskauer Papyrus. Der Papyrus hat eine Länge von 5,5 Metern und eine Breite von 8 cm. Das Dokument ist in hieratischer Schrift verfasst worden und enthält 25 Aufgaben.
Der Papyrus Moskau wurde von Vladimir Semionovitsch Golenischeff 1893 erworben. Der russische Ägyptologe unternahm etwa. 60 Reisen nach Ägypten. Seine gesammelten Antiquitäten, wie der Papyrus Moskau oder auch literarische Papyri, schenkte er 1911 dem Museum von Moskau.
Man findet eine Näherung für π durch Aufgabe 10 in dem Papyrus. Diese Aufgabe behandelt die Berechnung einer Korboberfläche durch eine Volumenberechnung. Aus dem Originaltext (siehe Originaltext) dieser Aufgabe ergibt sich die folgende Berechnungsformel, wobei die Größe d für den Öffnungsdurchmesser des Korbes und damit den Durchmesser des Halbkugelbodenkreises steht.

A = 2 · d · 8/9 · 8/9 · d = 128/81 · d² = 2 · (256/81) · r²

Daraus ergibt sich folgende Näherung für π

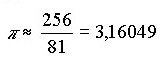Papyrus Rhind

Das Papyrus Rhind wurde 1858 von dem schottischen Juristen A. H. Rhind erworben und hat daher seinen Namen. Die Papyrusrolle wurde bei illegalen Grabungen am Ramesseum entdeckt.
Der Papyrus Rhind hat eine Länge von etwa 5,5 Meter und ist ca. 32 cm breit. Er wurde in hieratischer Schrift vom Schreiber Ahmose (auch Ahmes) um das Jahr 1650 v. Chr. (Zweite Zwischenzeit - Fremdherrschaft der Hyksos - 17. Dynastie) als Kopie einer 200 Jahre älteren Schrift angefertigt und enthält 87 mathematische Textaufgaben mit beispielhaften Lösungen, sowie Tafeln mit Brüchen.
In der Aufgabe 48 wird die Fläche eines Kreises berechnet, der einem Quadrat mit einer Seitenlänge von 9 Einheiten eingeschrieben ist. Dazu existiert im Papyrus, außer dem Rechenweg, noch eine kleine Skizze, aus der sich rekonstruieren lässt wie die Ägypter zu einem Näherungswert für π kamen.

Dazu werden zunächst die Seiten des Quadrats in drei Teile geteilt und man erhält so neun kleinere Quadrate. Dann schneidet man von den vier Eckzellen jeweils die Hälfte weg und erhält damit ein unregelmäßiges Achteck. Dieses Achteck wird im Papyrus Rhind als Näherung für die Kreisfläche genommen.

Dieses Achteck (mit der Gesamtfläche von 7 kleinen Quadraten) besitzt den Flächeninhalt von 63 Flächeneinheiten und ist, nach Meinung des Schreibers, etwas kleiner als die Fläche des Kreises. Die dann mit 64 Flächeneinheiten angenommen wird. In moderner Schreibweise:

A_Kreis= 64 = (4,5)² · π
A_Kreis= 8² = (9/2)² · π
π = 8²/(9/2)² = (16/9)²

In der Aufgabe 50 wird für eine Fläche des Kreises mit dem Durchmesser 9 als Lösung das Quadrat mit der Seitenlänge 8 angegeben. In beiden Aufgaben wird für π die folgende Näherung benutzt:

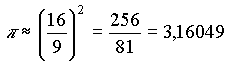Der Papyrus befindet sich seit 1865 unter den Inventarnummern pBM 10057 und pBM 10058 im Britischen Museum in London. Abgesehen von einigen kleinen Fragmenten, die nicht von Rhind erworben wurden und die heute im Brooklyn Museum in New York gelagert werden.

Es könnte aber auch schon vor der Abfassung des Papyrus Rhind bessere Näherungswerte gegeben haben: POSAMENTIER (The Mathematics Teacher v. 77(1); S.52,47) führt das Buch "La Science Mystérieuse des Pharaons" von Abbé Moreux (Paris 1923) an, wo auf den Seiten 28-29 eine vermutete Näherung von 3,14159294 angegeben wird. (zitiert nach Mäder 1989, S.55)

1.1.2

Babylonien

Historisch nachgewiesen, durch entsprechende Funde von Keilschrifttafeln, ist dass den Babylonier auf algebraischem Gebiet die vier Grundrechenarten und das Lösen von einfachen Gleichungssystemen vertraut waren.

Neben dem Algorithmus für die Berechnung von Quadratwurzeln, legten sie Zahlentabellen an z. B. für Quadrate, Kuben, Quadratwurzeln, Kubikwurzeln, Logarithmen, pythagoreische Zahlen.

In der Geometrie waren die allgemeinen Regeln zur Flächen- und Volumenberechnung bekannt. Die Babylonier benutzten den Satz des Pythagoras und kannten auch den Halbkreis des Thales.
Eine mathematische Beweisführung jedoch wurde von den Babyloniern offenbar nicht angestrebt, da sie sich nur unter praktischen Gesichtspunkten für Mathematik interessierten.

Etwa zur selben Zeit wie in Ägypten (1900-1600 v.Chr.) sind auch schon in Babylonien erste Näherungen für π dokumentiert.

Der Wert 3 wurde als solche Näherung benutzt. Dieser könnte durch Einschreiben eines 12-Ecks in den Einheitskreis entstanden sein

Keilschrifttexte, die 1936 in Susa entdeckt wurden, geben für π diesen Wert an:

1.1.3

Bibel und Talmud

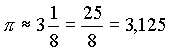In der Bibel im ersten Buch der Könige, Kapitel 7, Vers 23 (siehe auch zweites Buch der Chronik, 4, 2-5) wird berichtet, das ein Bronzeschmied aus Tyros Arbeiten für König Salomo ausgeführt haben soll: „Dann machte er das Meer. Es wurde aus Bronze gegossen und maß 10 Ellen von einem Rand zum anderen; es war völlig rund und 5 Ellen hoch. Eine Schnur von 30 Ellen konnte es rings umspannen.“
Anhand dieses konkreten Beispiels lässt sich ein Verhältnis von Durchmesser zu Radius mit dem Wert 3 für π ermitteln.

Im Talmud heißt es: "Was im Umfange drei Handbreiten hat, ist eine Hand breit." Auch hier wird für π der Wert 3 angenommen.

Diese Informationen aus Bibel und Talmud entstammen etwa der Zeit 500 v. Chr.

In J. Wiesenbauers Buch "Algorithmen zur numerischen Berechnung von π" wird auf Seite 301 angegeben das der Rabbi Nehemiah etwa 150 n.Chr. bereits den Wert von Archimedes für π mit 3 1/7 kannte

1.1.4

Die Griechen und die Quadratur des Kreises

Die Quadratur des Kreises war eines der Lieblingsthemen der alten Griechen. Die Aufgabe war, zu einem gegebenen Kreis, nur mit Hilfe von Lineal und Zirkel, ein umfang bzw. flächengleiches Quadrat zu konstruieren.
Dieses sollte in einer begrenzten Anzahl von Schritten bewältigt werden. Aus noch zu ersehenden Gründen ist dies geometrisch exakt aber unmöglich.

Antiphon (430 v.Chr.) war der Meinung, daß die Quadratur des Kreises und damit die exakte Bestimmung von π möglich sein müsse, weil sich jedes Polygon in ein Quadrat verwandeln läßt.
Seine Idee ging davon aus, dem Kreis Vielecke mit immer größerer Seitenzahl einzuschreiben, so das diese schließlich nicht mehr vom Kreis zu unterscheiden sind und damit der Kreis völlig "erschöpft" ist. Auf Grund dieser Vorgehensweise nennt man diese Technik Exhaustions-Methode Der lateinische Ausdruck heißt "exhaurire", was herausnehmen, erschöpfen, vollenden bedeutet.
Damit legte Antiphon den Grundstein für die erfolgreiche Arbeit vieler Mathematiker in späterer Zeit, nicht zuletzt des Archimedes, derauf diese Methode zurück griff.

Bryson aus Heraklea ging noch einen Schritt weiter und berechnete die Fläche von zwei Vielecken – eines das den Kreis von innen begrenzte und eines zweiten das den Kreis von außen umschloss. Die Fläche des Kreises, so folgerte Bryson, müsse zwischen den Flächen der beiden Vielecke liegen.
Damit legten Antiphon und Bryson den Grundstein für die erfolgreiche Arbeit vieler Mathematiker in späterer Zeit, nicht zuletzt des Archimedes, der dann eben diese Methode anwandte.

Euklid von Alexandria (325-265 v. Chr.) gelang der Beweis, daß 3 < π < 4 gilt. Doch erst Archimedes konnte rund 100 Jahre später diese Ungleichung verfeinern.

Siehe dazu auch: Geschichte der Quadratur

1.1.5

Archimedes

Archimedes von Syrakus (287-212 v. Chr.) war Mathematiker, Physiker und Ingenieur. Er gilt als einer der bedeutendsten Mathematiker der Antike, der u.a. die Gesetze für den Auftrieb, den Hebel und den Flaschenzug fand. Eine ausführliche Abhandlung von Archimedes mit dem Titel „Kreismessung“ ist dokumentarisch überliefert. Archimedes beweist in seiner Arbeit drei grundlegende Sätze:

Satz 1: Die Fläche eines Kreises ist gleich der Fläche eines rechtwinkligen Dreiecks, mit dem Kreisradius als der einen und dem Kreisumfang als der anderen Kathete.

Berechnen lässt sich die Kreisfläche dann als

A_Kreis = ½ · Radius · Umfang

Archimedes beweist den Satz indirekt. Indem er die Fläche des Kreises einmal als größer und einmal als kleiner als die Dreiecksfläche annimmt. Beide Aussagen werden dann zum Widerspruch geführt. Die Konsequenz ist daher, dass die Kreisfläche nur gleich der Dreiecksfläche sein kann.

Nach heutiger Sicht hat Archimedes mit diesem Satz das Problem der Quadratur des Kreises auf die Frage nach der Konstruierbarkeit des Umfangs eines Kreises (aus dem vorgegebenen Radius) zurückgeführt. Und damit auf die Konstruierbarkeit von &api;.
Mit diesem Satz taucht auch hier wieder unvermittelt ein Wissen auf, dass schon länger bekannt gewesen sein muss bzw. für das es Vorläufer gegeben haben muss. In diesem Satz verborgen steckt das Wissen das die Kreisfläche proportional zum Produkt aus Radius und Umfang ist.

Wie zu sehen war, lässt sich die Proportionalität von Kreisfläche und Durchmesserquadrat schon aus der Aussage von Antiphon folgern. Das ließe sich allgemein so formulieren:

A_Kreis = d² · Faktor1

Man kann voraus setzen das eine Rektifikation des Kreises bekannt war, und damit auch diese Beziehung

U_Kreis = d · Faktor2

Bildet man das Produkt Durchmesser mal Umfang dann ergibt sich:

d · U_Kreis = d · (d · Faktor2) = d² · Faktor2

Also ist das Rechteck aus Durchmesser (Radius) und Umfang auch proportional zum Durchmesserquadrat bzw. zur Kreisfläche. Das müsste schon zu Zeiten Antiphons bekannt gewesen sein. Und ohne zu wissen das es nur einen einzigen Proportionalitätsfaktor gibt.
Außerdem ist in dem Satz über die Kreisfläche auch das Wissen enthalten das bei Rektifikation und Quadratur des Kreises nur ein Proportionalitätsfaktor nämlich π existiert. Hier könnte es ebenfalls Vorläufer gegeben haben, denn diese Zusammenhänge sind auch in der Rektifikationskonstruktion über das 14:11 Dreieck enthalten, wenn man diese zur Quadratur erweitert. Die von Archimedes angegebene Gleichung:

A_Kreis = ½ · Radius · Umfang

Durch eine kleine Umstellung der Gleichung entsteht:

A_Kreis = Radius · Umfang/2

Und dies lässt sich unmittelbar als ein Rechteck interpretieren, mit den Seitenlängen r und U/2. Dieses Rechteck lässt sich auch direkt aus der Rektifikationskonstruktion über das 14:11 Dreieck ableiten. Siehe Quadratur 1

Quadrat und Kreis besitzen den gleichen Umfang, also ist eine Quadratseite gleich U/4.

Durch Anlegen einer Quadratseite an eine zweite Quadratseite entsteht eine Strecke mit der Länge U/2.

Das blaue Rechteck ist dann das Rechteck Radius mal Umfang Halbe und entspricht also der Kreisfläche.

Durch die komplette Abwicklung des Umfanges lässt sich das archimedische Dreieck dann leicht konstruieren.

Insgesamt ist die Konsequenz das die Beziehung A_Kreis ≈ Radius · Umfang also schon länger bekannt gewesen sein muss.
Es ist daher sehr wahrscheinlich das Archimedes, genau wie Thales und Pythagoras, bei seinem ersten Satz aus dem Fundus der allgemein bekannten Überlegungen und Konstruktionen schöpfte.
Die Genialität liegt darin das er als Erster eine exakte Gleichung für die Kreisfläche angeben konnte und diesen Sachverhalt durch ein rechtwinkliges Dreieck derart darstellte, das Umfang und Fläche des Kreises so miteinander verknüpft sind, das nur ein Proportionalitätsfaktor (nämlich π) existiert.

Satz 3: Der Umfang eines Kreises ist größer als 3 10/71 und kleiner als 3 1/7 des Durchmessers.

Daraus folgt direkt:

bzw.

Archimedes greift hier den Gedanken von Bryson auf, nämlich der beliebigen Annäherung des Kreises durch eingeschriebene und umschreibende regelmäßige Vielecke. Ausgehend vom eingeschriebenen Sechseck und einem umschreibenden Dreieck gelangt Archimedes, durch sukzessive Verdoppelung der Seitenzahl, jeweils bis zum 96-Eck.
Eine Abschätzung der in den einzelnen Rechenschritten auftretenden Quadratwurzeln ergibt die genannten Schranken. Und gleichzeitig wird, durch die obere Schranke der Ungleichung, eine ebenso einfache wie genaue Näherung dieser Zahl, nämlich 22/7 angegeben. Ein Wert, der für praktische Zwecke, bis heute Verwendung findet.

Archimedes liefert damit als Erster ein vollständiges Verfahren zur Ermittlung der Kreiszahl. Dieses Verfahren war bis ins 17. Jahrhundert praktisch das wichtigste Verfahren zur Bestimmung der Kreiskonstanten. Erst mit der Arbeit von Huygens war der rein geometrische Ansatz zur Bestimmung der Kreiszahl im wesentlichen ausgeschöpft.

Satz 2: Die Fläche eines Kreises verhält sich zum Quadrat seines Durchmessers nahezu wie 11/14.

Also:

A_Kreis = d² · 11/14

Der zweite Satz ist eine Folgerung aus den beiden anderen Sätzen. Das sich die Fläche eines Kreises proportional zum Quadrat seines Durchmessers verhält, war ja bereits seit Antiphon bekannt und erstmals 100 Jahre zuvor von Euklid angegeben worden. Archimedes gibt hier als Erster explizit den Wert der Proportionalitätskonstanten mit 11:14 an.

Mit den drei Sätzen des Archimedes ist auch die Rektifikation des Kreises also die Umfangsbestimmung eindeutig gegeben. Es gilt:

A_Kreis = ½ · Radius · Umfang = ½ · r · U = ¼ · d · U
A_Kreis = d² · 11/14 = r² · 22/7

Zusammen genommen ergibt sich:

¼ · d · U = A_Kreis = d² · 11/14

Umstellen der Gleichung zum Umfang hin ergibt:

U = d · 11/14 · 4 = d · 22/7

U = d · 22/7 = r · 44/7 ==> π = 22/7

In einer weiteren Arbeit „Über Spiralen“ beschreibt Archimedes die Konstruktion der später nach ihm benannten Spirale, die durch die Überlagerung einer kreisförmigen mit einer linearen Bewegung gewonnen wird.
Er zeigt, dass durch das Anlegen der Tangente an diese Spirale der Umfang eines Kreises auf einer Geraden abgetragen werden kann.
Auf die damit geleistete Quadratur des Kreises verweisen erst spätere Kommentatoren hin. Archimedes selbst macht hierzu keine Aussage. Wie bei der Quadratrix sind weder die Spirale selbst noch ihre Tangente mit Zirkel und Lineal konstruierbar.

1.1.6

Heron von Alexandria

Heron von Alexandria (10-75 n. Chr.) war Mathematiker, Ingenieur und Erfinder. Seine Lebensdaten lassen sich nur ungenau ermitteln. Er muss nach Archimedes, aber vor Pappos gelebt haben, d.h. etwa zwischen 200 v. Chr. und 300 n. Chr.
Heron lehrte am Museion von Alexandria, das berühmt für seine Bibliothek war. Seine Werke sind teilweise nur fragmentarisch überliefert; offenbar handelt es sich zum Teil um Vorlesungsnotizen. Sie beschäftigen sich unter anderem mit mathematischen, optischen und mechanischen Themen. Bekannt sind vor allem seine Ausführungen zu automatischen, teilweise sogar schon programmierbaren Geräten und der Ausnutzung von Wasser, Luft und Hitze als treibende Kraft. Hier sind insbesondere die Erfindung der Aeolipile, auch Heronsball genannt, und der Heronsbrunnen zu nennen.
Er fand u.a. das Heron-Verfahren zum Berechnen der Quadratwurzel, sowie den Satz des Heron, der es erlaubt, den Flächeninhalt eines Dreiecks nur mit Kenntnis der drei Seiten zu berechnen. (ohne Winkel oder andere Teile des Dreiecks zu kennen)
In einem der zahlreichen Bücher mit Namen Metrika („Buch der Messung“) liefert der Gelehrte den Beweis zur später nach ihm benannten Heronschen Formel. Auch die Bezeichnung Heronisches Dreieck erinnert an den antiken Mathematiker.

Nach Angaben von Heron von Alexandria soll Archimedes sogar eine noch bessere Abschätzung für π gefunden haben. Es ist aber nicht vollständig geklärt, ob dieser Ausdruck wirklich von ihm stammt. Seine Angabe lautet:

1.1.7

Apollonius von Perge

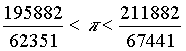Apollonius von Perge (262-190 v. Chr.) war Mathematiker. Sein bedeutendstes Werk "Über Kegelschnitte" beschäftigt sich in eingehenden Untersuchungen über die Problematik der Kegelschnitte. Er wies nach, dass die drei verschiedenen Kegelschnitte (Ellipse, Parabel und Hyperbel), deren Namen und Definitionen er einführte, vom selben allgemeinen Kegeltypus stammen. Nach Apollonios von Perge sind auch der Kreis des Apollonios und das Apollonische Problem benannt.
In der Astronomie trug Apollonios zur Epizykeltheorie bei und zeigte deren Verbindung zur Exzenter-Theorie. Er erklärte damit die rückläufige Planetenbewegung und die Bewegung des Mondes. Seine Theorien wurden unter anderem von Hipparchos und Claudius Ptolemäus aufgegriffen und weiterentwickelt.
Über sein Leben ist nur wenig bekannt. Er studierte und arbeitete in Alexandria unter Ptolemaios III. und Ptolemaios IV., besuchte Kleinasien und lebte für kurze Zeit in Pergamon.

Auf Apollonius geht folgender Wert für π zurück:

1.1.8

Claudius Ptolemäus

Claudius Ptolemäus, lateinisch Claudius Ptolomaeus (um 100, möglicherweise in Ptolemais Hermeiou, Ägypten bis vor 180, vermutlich in Alexandria), war ein griechischer Mathematiker, Geograph, Astronom, Astrologe, Musiktheoretiker und Philosoph. Ptolemäus wirkte als Bibliothekar an der berühmten antiken Bibliothek in Alexandria. Insbesondere seine drei Werke zur Astronomie, Geografie und Astrologie galten in Europa bis in die frühe Neuzeit als wichtige umfangreiche Datensammlungen und wissenschaftliche Standardwerke.
So schrieb Ptolemäus die Mathematike Syntaxis („mathematische Zusammenstellung“), später Megiste Syntaxis („größte Zusammenstellung“), heute Almagest (abgeleitet vom Arabischen al-magist) genannte Abhandlung zur Mathematik und Astronomie in 13 Büchern. Sie war bis zum Ende des Mittelalters ein Standardwerk der Astronomie und enthielt neben einem ausführlichen Sternenkatalog eine Verfeinerung des von Hipparchos von Nicäa vorgeschlagenen geozentrischen Weltbildes, das später nach ihm Ptolemäisches Weltbild genannt wurde.
Claudius Ptolemaeus nützte die Vorarbeit des Archimedes und setzte dessen Methode bis zum 720-Eck fort. Damit erreichte er für π die Näherung :

1.1.9

Karpos von Antiochia

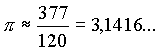Karpos von Antiochia war Astronom und Mathematiker des 1. oder 2. Jahrhunderts n. Chr. Er verfasste ein heute verlorenes Werk (Astrologike pragmateia), das bei Proklos zitiert wird.
Dort behauptet er den Vorrang der visuellen Evidenz von Konstruktionen gegenüber der formalen Ableitung von Lehrsätzen. Da er dort auch Mechaniker genannt wird, kann angenommen werden, dass er sich mit der Konstruktion astronomischer Instrumente beschäftigte.

Darüber hinaus befasste er sich mit der Quadratur des Kreises. Seine Konstruktionen sind, wegen des Verlustes, heute nicht mehr nachvollziehbar, ähneln jedoch der Quadratrix des Hippias und der Spirale des Archimedes.

Wie in manchen anderen gesellschaftlichen und kulturellen Bereichen gab es auch in der Mathematik in den westlichen Kulturen eine sehr lange Zeit der Stagnation nach Ende der Antike und während des Mittelalters. Fortschritte in der Annäherung an π erzielten in dieser Zeit vor allem chinesische und persische Wissenschaftler.
Im dritten Jahrhundert bestimmte Liu Hui – ähnlich wie Archimedes – die Schranken 3,1410 und 3,1427. Um 480 berechnete der chinesische Mathematiker und Astronom Zu Chongzhi (430–501) für die Kreiszahl 3,1415926 < π < 3,1415927, also im Grunde die ersten 7 Dezimalstellen exakt. Er kannte auch den fast genauso guten Näherungsbruch 355/113 (das ist der dritte Näherungsbruch der Kettenbruchentwicklung von π), der in Europa erst im 16. Jahrhundert gefunden wurde.

Wang Fan

Von Wang Fan um 250 n.Chr. stammt die Näherung:

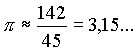Liu Hui

Liu Hui (220 bis 280) war ein chinesischer Mathematiker. Er lebte im Wei-Reich. Liu Hui ist bekannt für seine Kommentare zu den Jiuzhang Suanshu, den „Neun Büchern arithmetischer Technik“. Dies ist eine Sammlung zur Lösung mathematischer Probleme aus dem Alltagsbereich. Liu Hui veröffentlichte das Jiuzhang Suanshu im Jahre 263 mit eigenen Kommentaren, das ist gleichzeitig die älteste erhaltene Ausgabe. Zu seinen herausragendenden Arbeiten gehören.
Die Lösung linearer Gleichungssysteme mit Hilfe eines Verfahrens, das später als Gaußsches Eliminationsverfahren bekannt wurde. Die Berechnung der Volumina von Prisma, Pyramide, Tetraeder, Zylinder, Kegel und Kegelstumpf.
Außerdem verfasste er das Haidao suanjing („Mathematisches Handbuch der Seeinsel“), eines der zehn Klassiker (Suanjing shi shu) der mittelalterlichen chinesischen Mathematik. Es wurde 263 geschrieben und enthält Methoden für die Landvermessung, die in den folgenden tausend Jahren in Ostasien nach diesem Buch verwendet wurden.
Liu Hui bestimmte aus dem 192-Eck die Schranken 3,141024 und 3,142704, später aus dem 3072-Eck den Näherungswert 3,14159. Er schlug 3,14 als gute Näherung vor.

Tsu Chu'ung-Chi

Der Astronom Tsu Chu'ung-Chi (430-501 n.Chr.) und sein Sohn Tsu Keng-Chi fanden diese Näherung:

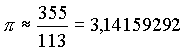Tsu Ch’ung Chi (Zu Chong Zhi) wurde als Mathematiker und Astronom bekannt und war etwa 800 Jahre lang der Weltrekordhalter in der Präzision der Darstellung von π.
Die Wissenschaftshistoriker wissen nicht sehr viel über ihn. Insbesondere ist rätselhaft, wie Tsu seine erstaunliche Approximation der Kreiszahl π berechnet hat. Wahrscheinlich benutzten sie eingeschriebene Polygone, die bis zu 24576 Seiten enthielten.
Über den Ursprung dieses einfachen Bruches gibt es nur Vermutungen, die besagen, das Tsu einfach die bekannten Brüche von Ptolemäus und Archimedes verwendet hat. Indem er die Differenz der Zähler und Nenner bildete:

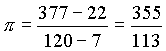Um 500 v.Chr. waren für π Näherungen in Gebrauch, wie zum Beispiel:

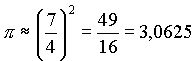Noch öfter findet man einen Wert, der auch als Hinduwert bezeichnet wird:

Brahmagupta

Brahmagupta (598 bis 668) war ein indischer Mathematiker und Astronom. Er leitete das astronomische Observatorium in Ujjain und verfasste in dieser Funktion zwei Arbeiten zur Mathematik und zur Astronomie, das Brahmasphutasiddhanta im Jahre 628 und das Khandakhadyaka im Jahre 665.
Das Brahmasphutasiddhanta ist, wenn man vom Zahlensystem der Mayas absieht, der früheste bekannte Text, in dem die Null als geschriebene Zahl behandelt wird. Zuvor hatten im 6. Jahrhundert v. Chr. bereits die Babylonier den Wert Null als Leerzeichen verwendet.
Darüber hinaus stellte Brahmagupta in diesem Werk Regeln für die Arithmetik mit negativen Zahlen und mit der Zahl 0 auf, die schon weitgehend unserem modernen Verständnis entsprechen. Der größte Unterschied bestand darin, dass Brahmagupta auch die Division durch 0 zuließ, während in der modernen Mathematik Quotienten mit dem Divisor 0 nicht definiert sind.
Zu seinen bekanntesten Resultaten gehören zwei nach ihm benannte Lehrsätze über Sehnenvierecke. Der Satz von Brahmagupta, der eine Seitenhalbierung in bestimmten Sehnenvierecken beschreibt und die Formel von Brahmagupta, die die Fläche eines beliebigen Sehnenvierecks berechnet. Auf ihn geht auch die Brahmagupta-Identität zurück.
Brahmagupta fand 640 n.Chr. ebenfalls den sogenannten Hinduwert, indem er die Summe der Seitenlängen von 12-, 24-, 48- und 96-seitigen Polygonen berechnete.

Aryabhatiya

Aryabhatiya (476 in Ashmaka bis um 550) war ein bedeutender indischer Mathematiker und Astronom. Geboren in Ashmaka, lebte er später in Kusumapura, das später Bhaskara I. (629) als Pataliputra, das heutige Patna identifizierte.
Es wird vermutet, dass das Konzept der Zahl „0“ (Null) auf Aryabhata zurückgeht, wenngleich erst bei Brahmagupta die Null offensichtlich als eigenständige Zahl behandelt wird und dafür Rechenregeln angegeben sind.
Er konnte Quadratwurzeln und Kubikwurzeln ziehen sowie verschiedene lineare und quadratische Gleichungen lösen; er entwickelte auch die Trigonometrie weiter. Selbst seine Sinustafeln sind in alter indischer Tradition in Versform geschrieben. Als seine größte mathematische Leistung ist aber die „unbestimmte Analytik“ für verallgemeinerte diophantische Gleichungen anzusehen. Vermittelt durch muslimische Mathematiker gelangte sein mathematisches Wissen indirekt auch ins spätere mittelalterliche Europa.

Aryabhatiya bestimmte die Kreiszahl π für damalige Verhältnisse sehr genau auf 3,1416 und scheint schon geahnt zu haben, dass es sich um eine irrationale Zahl handelt.
Seine Näherung, die auch im Paulisha Siddhanta erwähnt wird:

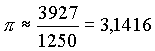Zur Geschichte der Approximation der Zahl Pi - Teil 1

Die Zahl Pi im Altertum