DIE QUADRATUR DES KREISES ALS NÄHERUNGSLÖSUNG
Copyright © Klaus Piontzik
| 1.2.0 | Arabien | 1000 - 1430 | |
| 1.2.1 | Franco von Lüttich | 1015 - 1083 | |
| 1.2.2 | Fibonacci | 1180 - 1241 | |
| 1.2.3 | Nikolaus von Kues | 1401 -1464 | |
| 1.2.4 | Albrecht Dürer | 1471 - 1528 | |
| 1.2.5 | Tycho de Brahe | 1546 - 1601 | |
| 1.2.6 | Francois Viete | 1540 - 1603 | |
| 1.2.7 | Adriaen Metius | 1571 - 1635 | |
| 1.2.8 | Valentius Otho | 1548 - 1603 | |
| 1.2.9 | Ludolph von Ceulen | 1540 -1610 | |
| 1.2.10 | Adriaan van Roomen | 1561 - 1615 | |
| 1.2.11 | Christoph Grienberger | 1561 - 1636 | |
| 1.2.12 | Snellius | 1580 - 1626 | |
| 1.2.13 | Christiaan Huygens | 1629 - 1695 | |
| 1.2.14 | Thomas Hobbes | 1588 -1679 | |
| 1.2.15 | Adam Kochanski | 1631 - 1700 | |
| 1.2.16 | Jacob Marcelis | 1640 - 1780 | |
| 1.2.17 | Popularität der Kreisquadratur | ||
Ibn al-HeithemAlhazen auch Ibn al-Heithem, latinisiert Alhacen, Avennathan oder Avenetan, (965 - 1040), war ein Mathematiker, Optiker und Astronom in der Blütezeit des Islam. Er verfasste grundlegende Beiträge zur Optik, Astronomie, Mathematik und Meteorologie.Ibn al-Heithem behandelte selbständig die Quadratur des Kreises. Dschamschid Mas ud al-KaschiGhiyath ad-Din Dschamschid bin Masud bin Muhammad al-Kaschi (1380 - 22. Juni 1429) war ein persischer Arzt, Mathematiker und Astronom des Hochmittelalters. In Frankreich wird der Kosinussatz als Théorème d’Al-Kashi bezeichnet.Er stellte aufbauend auf dem Zij-i Ilkhani (Tabelle der Ilchane) des at-Tusi einen neuen Sternkatalog zusammen, der auch eine Sammlung mathematischer Gleichungen für die Astronomie wie Formeln für die Transformation von ekliptikalen zu äquatorialen Koordinaten und Tafeln trigonometrischer Funktionen enthielt. Er ist bekannt als Khagani Zij, Tafeln des Khans, da er ihn entweder dem Timuriden-Fürsten Schah Ruch oder dessen Sohn Ulug Beg widmete. Ulug Beg erkannte die außergewöhnlichen Fähigkeiten Al-Kashis und berief ihn 1420 an seine neugegründete Madresse in Samarkand. Er war der wichtigste Berater bei Konzeption und Bau des der Madresse angegliederten Observatoriums Gurkani Zij. Lange unübertroffene Ergebnisse wurden von ihm durch numerische Lösungen erbracht. Im ar-Risala al-Muhitiya (Lehrbrief über den Kreisumfang) bestimmte er beispielsweise den Umfang des Einheitskreises (also das doppelte der Kreiszahl π) aus dem 3*228-Eck auf 9 Sexagesimalstellen: 6;16,59,28,01,34,51,46,14,50, die er in die indischen Ziffern 6,2831853071795865 mit 16 richtigen Dezimalstellen umrechnete. Dies ist eines der ältesten Dokumente des Rechnens mit Dezimalbrüchen. Damit verbesserte er das Ergebnis des chinesischen Mathematikers Zu Chong-Zhi, der π auf 7 Stellen genau berechnet hatte. al-Kaschi wurde erst 1596 von Ludolph van Ceulen übertroffen, der nach 30 Jahren Arbeit 35 Dezimalstellen berechnet hatte. |
| In
Folge eines verstärkten Interesses für die antike
Mathematik im christlichen Europa ab etwa dem 11.
Jahrhundert entstanden etliche Abhandlungen über die
Quadratur des Kreises, jedoch ohne dass dabei wesentliche
Beiträge zur eigentlichen Lösung geleistet wurden. Als
Rückschritt zu betrachten ist, dass im Mittelalter der
Archimedische Näherungswert von 22/7 für die Kreiszahl
lange Zeit als exakt galt. Spätere Abhandlungen der Scholastik erschöpfen sich mehr oder minder in einer Abwägung der Argumente der bekannten Klassiker. Erst mit der Verbreitung lateinischer Übersetzungen der archimedischen Schriften im Spätmittelalter wurde der Wert 22/7 wieder als Näherung erkannt und nach neuen Lösungen des Problems gesucht |
| Franco
von Lüttich (zwischen 1015 und 1020 bis um 1083) war
einer der bedeutendsten Mathematiker des europäischen
11. Jahrhunderts. Franco studierte unter Adelmann (1000 - 1061) in Lüttich, wo er 1066 Leiter der Kathedralschule wurde. Er schrieb komputistische Traktate, die sog. „Geometrie II des Pseudo-Boethius“, die um 1035/47 entstand und die ersten vier Bücher der Elemente des Euklid enthielt, wurde ihm zugeschrieben. Das bekannteste Werk Francos ist indes seine Abhandlung über die Quadratur des Kreises, ein Werk von sechs Büchern, das vor 1050 niedergeschrieben wurde. Einer der ersten Autoren des Mittelalters, der das Problem der Kreisquadratur wieder aufnahm, war Franco von Lüttich. Um 1050 entstand sein Werk De quadratura circuli. Franco stellt darin zunächst drei Quadraturen vor, die er verwirft. Die ersten beiden geben für die Seitenlänge des Quadrates 7/8 beziehungsweise für die Diagonale 10/8 des Kreisdurchmessers an, was relativ schlechten Näherungen von 31/16 und 31/8 für π entspricht. Der dritte Vorschlag wiederum setzt den Umfang des Quadrates dem Kreisumfang gleich, verlangt also die Rektifikation des letzteren. |
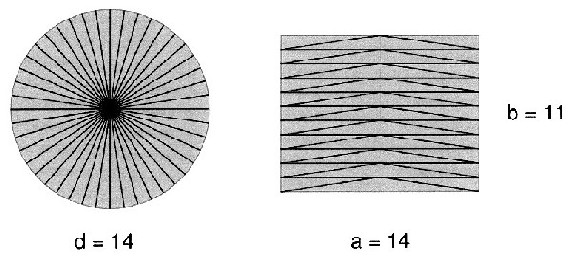
| Francos eigene
Lösung geht von einem Kreis mit Durchmesser 14 aus.
Dessen Fläche beträgt aus seiner Sicht genau 7² ? 22/7
= 154. Rechnerisch lässt sich nach Francos Argumentation
kein flächengleiches Quadrat finden, da die
Quadratwurzel aus 22/7 irrational ist, konstruktiv jedoch
schon. Dazu zerlegt er den Kreis in 44 gleiche Sektoren,
die er zu einem Rechteck der Seitenlängen 11 und 14
zusammenfügt. Den nötigen Kunstgriff, bei dem er die Kreissektoren durch rechtwinklige Dreiecke mit Katheten der Länge 1 und 7 ersetzt, erläutert Franco allerdings nicht. Problematisch ist auch sein nicht ganz geglückter Versuch, das Rechteck anschließend durch eine geeignete Zerlegung in ein Quadrat zu überführen. Offensichtlich war Franco das althergebrachte griechische Verfahren nicht geläufig. |
| Leonardo
da Pisa, auch Fibonacci genannt
(um 1180 in Pisa bis nach 1241 ebenda) war Rechenmeister
in Pisa und gilt als der bedeutendste Mathematiker des
Mittelalters. Bekannt sind heute vor allem die nach ihm
benannten Fibonacci-Zahlen. Über die Biographie Leonardos ist nur wenig bekannt, die meisten Angaben gehen zurück auf den Widmungsprolog seines Rechenbuchs Liber abbaci und auf ein Dokument der Kommune von Siena. Von Leonardo sind noch einige weitere Werke erhalten: eine Practica geometriae von 1220 (1219), gewidmet einem Freund und Lehrer Dominicus, die im 15. Jahrhundert von Cristoforo Gherardo di Dino auch ins Italienische übertragen wurde; ein Liber quadratorum von 1225 (1224), der Friedrich II. gewidmet ist und erwähnt, dass dieser bereits ein Buch Leonardos gelesen habe, was man auf den Liber abbaci zu beziehen pflegt. Ferner eine nicht datierte Schrift Flos super solutionibus quarumdam questionum ad numerum et ad geometriam uel ad utrumque pertinentium, welche dem Kardinal Raniero Capocci von Viterbo gewidmet ist und Fragen behandelt, die Leonardo im Beisein Friedrichs II. von einem Magister Johannes aus Palermo vorgelegt worden sein sollen; und schließlich ein Brief an einen Magister Theodorus. Aus Leonardos Schriften geht hervor, dass er auch noch zwei weitere, heute nicht mehr erhaltene Schriften verfasste, ein kürzeres Rechenbuch und einen Kommentar zum zehnten Buch der Elemente Euklids. Circa 1220 errechnete Fibonacci 3.1418 für π indem er eine Polygon-Methode benutzte die auf Archimedes zurückgeht. |
| Nikolaus
von Kues, latinisiert Nicolaus Cusanus oder
Nicolaus de Cusa (1401 - 11. August 1464), war ein schon
zu Lebzeiten berühmter, universal gebildeter deutscher
Philosoph, Theologe und Mathematiker. Er gehörte zu den
ersten deutschen Humanisten in der Epoche des Übergangs
zwischen Spätmittelalter und Früher Neuzeit. Nikolaus verfasste mehr als 50 Schriften, davon etwa ein Viertel in Dialogform, die übrigen in der Regel als Abhandlungen, ferner rund 300 Predigten sowie eine Fülle von Akten und Briefen. Seine Werke lassen sich nach dem Inhalt in drei Hauptgruppen gliedern: Philoso-phie und Theologie, Kirchen- und Staatstheorie, Mathematik und Naturwissenschaft. Eine Sonderstellung nimmt seine kurze Autobiographie ein, die er 1449 schrieb. Er veranlasste selbst eine (allerdings unvollständige) Sammlung seiner Schriften, die in zwei Handschriften seiner Bibliothek in Kues vorliegt. Das mathematische und naturwissenschaftliche Werk des Cusanus ist vor allem von seinem Interesse an Wissenschaftstheorie und von seinen metaphysisch-theologischen Fragestellungen geprägt; er will von mathematischen zu metaphysischen Einsichten hinführen. Mit Analogien zwischen mathematischem und metaphysischem Denken befasst er sich in Schriften wie De mathematica perfectione („Über die mathematische Vollendung“, 1458) und Aurea propositio in mathematicis („Der Goldene Satz in der Mathematik“, 1459). Als sein mathematisches Hauptwerk gilt De mathematicis complementis („Über mathematische Ergänzungen“, 1453). Mit dem Problem der Kreisquadratur und der Berechnung des Kreisumfangs setzt er sich in mehreren Schriften auseinander, darunter De circuli quadratura („Über die Quadratur des Kreises“, 1450), Quadratura circuli („Die Kreisquadratur“, 1450), Dialogus de circuli quadratura („Dialog über die Quadratur des Kreises“, 1457) und De caesarea circuli quadratura („Über die kaiserliche Kreisquadratur“, 1457). Auch in De mathematica perfectione befasst sich Nikolaus mit diesem Problem. Er hält eine Kreisquadratur nur näherungsweise für möglich und schlägt dafür ein Verfahren vor. Mit seinem Dialog Idiota de staticis experimentis („Der Laie über Versuche mit der Waage“, 1450) gehört er zu den Wegbereitern der Experimentalwissenschaft. De correctione kalendarii („Über die Kalenderverbesserung“, auch: Reparatio kalendarii, 1436) handelt von der damals bereits dringend erforderlichen Kalenderreform, die jedoch erst im 16. Jahrhundert verwirklicht wurde. Spätere Abhandlungen der Scholastik erschöpfen sich mehr oder minder in einer Abwägung der Argumente der bekannten Klassiker. Erst mit der Verbreitung lateinischer Übersetzungen der archimedischen Schriften im Spätmittelalter wurde der Wert 22/7 wieder als Näherung erkannt und nach neuen Lösungen des Problems gesucht, so beispielsweise von Nikolaus von Kues. Dieser griff die Idee, den Kreis durch eine Folge regelmäßiger Vielecke mit wachsender Seitenzahl anzunähern, wieder auf, suchte im Gegensatz zu Archimedes jedoch nicht den Kreisumfang, sondern den Kreisradius bei vorgegebenem gleichbleibendem Umfang der Polygone zu bestimmen. Der daraus ermittelte Wert für die Kreiszahl liegt auch immerhin zwischen den von Archimedes gegebenen Grenzen. Die eigentlichen cusanischen Arbeiten zum Thema liefern deutlich schlechtere Näherungen und wurden damit zum Ziel einer Streitschrift des Regiomontanus, der die Ungenauigkeit der Berechnungen nachwies und die Beweise „als philosophische, aber nicht als mathematische“ bezeichnete. |
| Albrecht
Dürer der Jüngere (21.
Mai 1471 - 6. April 1528) war ein deutscher Maler,
Grafiker, Mathematiker und Kunsttheoretiker von
europäischem Rang. Er war ein bedeutender Künstler zur
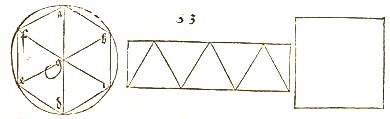
Zeit des Humanismus und der Reformation. Dürer hat für die Entwicklung des Holzschnittes und Kupferstiches Bedeutendes geleistet. Den Holzschnitt hat er aus dem „Dienst der Buchillustration” befreit und ihm den Rang eines eigenständigen Kunstwerks verliehen, das dem gemalten Bild an die Seite gestellt werden konnte. Dürer schuf durch Verfeinerung der Linien und eine Erweiterung des künstlerischen Vokabulars eine reichere Tonigkeit bzw. feinere Farbabstufungen und führte den Holzschnitt so formal in die Nähe des Kupferstichs. Wie den Holzschnitt so perfektionierte und revolutionierte Dürer auch die Techniken des Kupferstichs. Er wurde durch Blätter wie „Ritter, Tod und Teufel” und „Melencolia I” in ganz Europa bekannt. Dürer hat genau wie Tizian, Michelangelo und Raffael die Bedeutung der Druckgrafik darin gesehen, den eigenen künstlerischen Ruf zu verbreiten und durch den Vertrieb zu Einnahmen zu kommen. Benutzten die Italiener die Grafik zur Verbreitung ihrer Gemälde, so erhebt Dürer den Holzschnitt selbst zum Kunstwerk. Neben seinem künstlerischen Schaffen schrieb Dürer Werke über das Perspektivproblem in der Malerei, darunter Underweisung der Messung, und betätigte sich mit der Befestigung von Städten. Der „mathematischste Kopf” unter den Künstlern seiner Zeit war Albrecht Dürer. So erwarb er 1507 ein Exemplar der ersten Ausgabe der von Zamberti in das Lateinische übersetzten Elemente des Euklid von 1505, dem ersten Buchdruck dieses Werks überhaupt, und wirkte 1515 im Auftrag von Kaiser Maximilian I. an einer von dem Hofastronomen Johannes Stöberer entworfenen Karte der Erdhalbkugel mit („Stabius-Dürer-Karte”). Neben der im Papyrus Rhind erwähnten Gleichsetzung des Kreises vom Durchmesser 9 mit dem Quadrat der Seitenlänge 8 war auch die des Kreises vom Durchmesser 8 mit dem Quadrat der Diagonalen 10 bekannt. Diese Konstruktion findet sich bei den Babyloniern und eventuell beim römischen Feldmesser Vitruv. Um ein bequemes zeichnerisches Verfahren anzugeben, nimmt Albrecht Dürer diese Konstruktion im Jahr 1525 in seinem Werk Vnderweysung der messung mit dem zirckel und richtscheyt wieder auf. Dürer ist sich dabei bewusst, dass es sich um eine reine Näherungs-lösung handelt, er schreibt explizit, dass eine exakte Lösung noch nicht gefunden sei: „Vonnöten wäre zu wissen Quadratura circuli, das ist die Gleichheit eines Zirkels und eines Quadrates, also daß eines ebenso viel Inhalt hätte als das andere. Aber solches ist noch nicht von den Gelehrten demonstrirt. Mechanice, das ist beiläufig, also daß es im Werk nicht oder nur um ein kleines fehlt, mag diese Gleichheit also gemacht werden. Reiß eine Vierung und teile den Ortsstrich in zehn Teile und reiße danach einen Zirkelriß, dessen Durchmesser acht Teile haben soll, wie die Quadratur deren 10; wie ich das unten aufgerissen habe.“ |
| Tycho de
Brahe
auch bekannt als Tycho de Brahe (14. Dezember 1546 - 24.
Oktober 1601) war ein dänischer Adliger und einer der
bedeutendsten beobachtenden Astronomen. Zu seiner Zeit gab es noch kein Teleskop. Seine Beobachtungen der Fixstern- und Planeten-positionen, die damals mit Abstand die präzisesten waren und mit einer Genauigkeit von zwei Bogenminuten auch heute nicht ohne weiteres zu erreichen sind, führte er mit Hilfe eines großen Mauerquadranten durch. Aufgrund von Widersprüchen der Planetenbewegun-gen in den damals vorherrschenden Weltsystemen entwickelte er einen Kompromiss zwischen dem ptolemäisch-geozentrischen und dem kopernikanisch-heliozentrischen Planetensystem, das tychonisches Weltbild genannt wurde. Er beobachtete 1572 eine Supernova, einen „Neuen Stern“, wie er ihn beschrieb, „ein Wunder, wie es seit Anbeginn der Welt nicht gesehen wurde“. Dies machte ihn unter den Astronomen in ganz Europa berühmt. Tycho de Brahe nahm für π den Wert: |
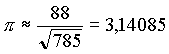 |
| Francois
Viete oder Franciscus Vieta, wie
er sich in latinisierter Form nannte (1540 in
Fontenay-le-Comte bis 13. Dezember, nach anderen Quellen
23. Februar 1603 in Paris), war ein französischer
Advokat und Mathematiker. Er führte die Benutzung von
Buchstaben als Variablen in die mathematische Notation
der Neuzeit ein. Eigentlich war die Mathematik für Viète nur eine Nebenbeschäftigung, trotzdem wurde er einer der wichtigsten und einflussreichsten Mathematiker seiner Zeit. Er wird manchmal auch „Vater der Algebra“ genannt, da er das Rechnen mit Buchstaben in der Neuzeit einführte und systematisch Symbole für Rechenoperationen benutzte, zumal er erkannte, dass dies weit mehr Möglichkeiten als bisher eröffnete. Viète hat zahlreiche Werke publiziert, die jedoch meistens nur in kleiner Auflage erschienen sind und für seinen Freundeskreis bestimmt waren. Die erste Gesamtausgabe wurde nach seinem Tod 1646 von Frans van Schooten in Leiden bei Elsevier unter dem Titel Opera mathematica, in unum volumen congesta, ac recognita, opera atque studio Francisci Schooten herausgegeben. Darüber hinaus hat er auf dem Gebiet der Trigonometrie Hervorragendes geleistet und wertvolle Vorarbeiten für die nachfolgende Ausarbeitung der Infinitesimalrechnung geleistet. Francois Viete drang 1579, in Fortsetzung der archimedischen Methode, bis zum 393216-Eck vor. Er erhielt eine Ungleichung, die den Wert für π bis auf 9 Dezimalstellen angab. Viete stellte erstmals eine geschlossene Formel für π vor, die sich aus einem unendlichen Produkt ableiten lässt. |
| Dieses Produkt fand Leonard Euler dann etwa 150 Jahre später. Die Konvergenz dieses Ausdrucks konnte aber erst F. Rudio im Jahre 1891 beweisen. |
| Adriaan
Metius Adriaan Adriaanszoon Metius
(9. Dezember 1571 - 6. September 1635) war ein
niederländischer Mathematiker, Landvermesser und
Astronom. Nach Metius wurde ein Mondkrater benannt. Metius publizierte Abhandlungen über das Astrolabium, über astronomische und mathemati-sche Themen. Er baute astrono mische Instrumente und entwickelte eine neue Variante des Jakobsstabs. Metius hielt nichts von der Astrologie, soll aber viel Zeit für alchemistische Studien und Experimente, vor allem bei Suche nach dem Stein der Weisen, verbracht haben. In seinem Buch Arithmeticæ et geometriæ practica , erschienen 1611 in Franeker, gab er den Wert für die Kreiszahl p mit 3,1415094 an. Bereits 1573 hatte Metius' Vater einen Annäherungswert für p berechnet. Mehr als 1000 Jahre nach Tsu Ch'ung-Chi entdeckte Adriaen Metius dieselbe Näherung 355/113, als er das arithmetische Mittel von Zähler und Nenner der beiden Näherungen 377/120 und 333/106, die auf Berechnungen seines Vaters beruhten, bildete. Beachtenswert ist hier, das durch den relativ einfachen Bruch insgesamt 4 Dezimalstellen von π anfallen: |
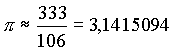 |
| Valentinus
Otho,
auch: Valentin Otto, Pitiscus, Parthenopolitanus (um 1548
- 8. April 1603) war ein deutscher Mathematiker. Über
seine Herkunft ist nichts bekannt. Nachdem er einige Zeit in Wittenberg geweilt, sich einem Studium der Astronomie, sowie der Mathematik gewidmet und Johannes Praetorius eine Abschätzung und eine Näherung für die Kreiszahl π vorgelegt hatte, begab er sich 1573 zu Georg Joachim Rheticus nach Kaschau in Oberungarn. In seinem 25. Lebensjahr gelangte er 1573 zu Meister Rheticus. Durch Valentinus Otho, wurde im Jahre 1573 die Näherung 355/113 bekannt. Rheticus begann Otho in seine Arbeiten einzuweihen. Jedoch erkrankte Rheticus 1574 und übertrug Otho kurz vor seinem Ableben die Aufgabe, sein großes trigonometrisches Werk zu vollenden und herauszugeben. Im Auftrag von Kaiser Maximilian II. stellte der kaiserliche Landeshauptmann Hans Rueber zu Pixendorf Otho zur Ordnung des Nachlasses von Rheticus ein. Um das Vermächtnis weiterführen zu können, folgte Otho 1577 einer Aufforderung des sächsischen Kurfürsten August, der ihn aus Kaschau als Professor der höheren Mathematik an die Universität Wittenberg berief. Nachdem Otho zwei Teile des Werkes fertig gestellt hatte, kam es 1581 zum Bruch mit der Wittenberger Hochschule. Nachdem er sich geweigert hatte, die Konkordienformel zu unterschreiben, entfernte man ihn aus seinem Amt. Otho wurde 1601 Professor der Mathematik an der Universität Heidelberg. |
| Ludolph
von Ceulen (28. Januar 1540 in
Hildesheim bis 31. Dezember 1610 in Leiden) war ein
deutscher Fechtmeister und Mathematiker, der in die
Niederlande auswanderte. Im 16. Jahrhundert erwachte dann auch in Europa die Mathematik wieder aus ihrem langen Schlaf. 1596 gelang es Ludolph van Ceulen, die ersten 35 Dezimalstellen von p zu berech-nen. Angeblich opferte er 30 Jahre seines Lebens für diese Berechnung. Van Ceulen steuerte allerdings noch keine neuen Gedanken zur Berechnung bei. Er rechnete einfach nach der Methode des Archimedes weiter, aber während Archimedes beim 96-Eck aufhörte, führte Ludolph diese bis zum eingeschriebenen 262-Eck fort. Der Name ludolphsche Zahl erinnert an seine Leistung. Hier sein Wert, der auch heute noch gültig ist: |
| π = 3,14159265358979323846264338327950288... |
| Ludolph van Ceulen widmete einen
großen Teil seiner Arbeit und seines Lebens der
Berechnung der Zahl π. 1596 errechnete er 20
richtige Stellen und kurz vor seinem Tod weitere 15.
Dabei diente ihm die Archimedische Methode als Grundlage.
Er benutzte ein- und umschriebene Polygone mit 262
Seiten. Die letzten drei der von ihm berechneten Ziffern
wurden in seinen Grabstein eingemeißelt. Daher wird p auch manchmal als Ludolphsche Zahl bezeichnet. |
| Adriaan
van Roomen
(29
September 1561 - 4 Mai 1615), auch bekannt als Adrianus
Romanus, war ein flämischer Mathematiker. Er stand mit Johann Reinhard Ziegler, Tycho Brahe und Johannes Kepler in Verbindung. Kepler traf er 1600 in Prag. Bekannt ist er auch durch einen Wettstreit mit François Viète. Aus Freundschaft mit Ludolph van Ceulen erwuchs seine Beschäftigung mit der Bestimmung von π, das er 1593 auf 16 Dezimalstellen bestimmte. |
| Christoph
Grienberger (auch Gruemberger, Grünberger) (2. Juli
1561 - 11. März 1636) war ein österreichischer
Jesuitenpater und Astronom. Grienberger schrieb optische und mathematische Werke. Er führte einen Briefwechsel mit vielen Persönlichkeiten seiner Zeit, vor allem mit seinen Mitbrüdern. In den Briefen beschäftigte er sich mit mathematischen und optischen Problemen. Zu seinen Schriften gehört ein ’’Neuer Fixsternkatalog’’ und ein ’’Neues Himmelsbild’’. 1630 errechnete Christoph Grienberger 39 Ziffern für π. Das ist bis heute die genaueste Annäherung durch manuell verwendende polygonale Algorithmen. |
| Willebrord
van Roijen Snell (auch Willebrordus Snel van Royen oder
Snellius; 13. Juni 1580 - 30. Oktober 1626), war ein
niederländischer Astronom und Mathematiker. Er ist bekannt für die Entwicklung des optischen Brechungsgesetzes, nach ihm als snelliussches Brechungsgesetz bezeichnet. Er gebrauchte den Namen Snellius für wissenschaftliche Veröffentlichungen. In Leiden folgte er 1613 seinem Vater Rudolph Snellius (1546–1613) als Professor für Mathematik an der dortigen Universität. 1615 entwickelte er mit der Triangulation eine neue Methode, den Umfang und den Radius der Erde zu ermitteln, die er in seinem 1617 veröffentlichtem Werk Eratosthenes Batavus beschrieb. In seinem Tiphys batavus, veröffentlicht 1624, beschäftigte er sich mit dem Problem der Meridianeinteilung und den daraus resultierenden Folgen für die Navigation. Er schrieb zudem zahlreiche weitere Werke über Mathematik, Astronomie und Landesvermessung. Snell veröffentlichte eine Lösung zur Pothenotschen Aufgabe, der Aufgabe des ebenen Rückwärtsschnitts. Ebenso verbesserte er die Exhaustionsmethode zur Berechnung der Kreiszahl π. Bei der ursprünglichen Methode des Archimedes wird der Kreisumfang durch den Umfang eines dem Kreis einbeschriebenen und den eines dem Kreis umbeschriebenen Vielecks abgeschätzt. Genauere Schranken ergeben sich durch eine Erhöhung der Eckenzahl. Der niederländische Mathematiker Snellius fand heraus, dass auch ohne die Seitenzahl zu vergrößern feinere Schranken für die Länge eines Bogenstückes als nur die Sehnen der Polygone angegeben werden können. Er konnte dieses Ergebnis allerdings nicht streng beweisen. |
| Christiaan
Huygens (14. April 1629 -
8. Juli 1695), auch Christianus Hugenius, war ein
niederländischer Astronom, Mathematiker und Physiker.
Huygens gilt, obwohl er sich niemals der noch zu seinen
Lebzeiten entwickelten Infinitesimalrechnung bediente,
als einer der führenden Mathematiker und Physiker des
17. Jahrhunderts. Er ist der Begründer der Wellentheorie
des Lichts, formulierte in seinen Untersuchungen zum
elastischen Stoß ein Relativitätsprinzip und
konstruierte die ersten Pendeluhren. Mit von ihm
verbesserten Teleskopen gelangen ihm wichtige
astronomische Entdeckungen. Huygens entdeckte mit seinem selbstgebauten Teleskop 1655 erstmals den Saturnmond Titan. Damit war der Saturn der zweite Planet nach dem Jupiter (von der Erde abgesehen), bei dem ein Mond nachgewiesen werden konnte (Galilei hatte schon 1610 die vier größten Jupitermonde entdeckt). Außerdem konnte er durch die bessere Auflösung seines Teleskops erkennen, dass das, was Galilei als Ohren des Saturns bezeichnet hatte, in Wirklichkeit die Saturnringe waren. Neben der Astronomie interessierte sich Huygens auch für die Mechanik. Er formulierte die Stoßgesetze und befasste sich mit dem Trägheitsprinzip und Fliehkräften. Seine Untersuchungen von Schwingungen und Pendelbewegungen konnte er zum Bau von Pendeluhren nutzen. Schon Galilei hatte eine solche entworfen, aber nicht gebaut. Huygens konnte seine Uhr hingegen zum Patent anmelden. Die in seinem Auftrag von Salomon Coster gebauten Uhren wiesen eine Ganggenauigkeit von zehn Sekunden pro Tag auf, eine Präzision, die erst hundert Jahre danach überboten werden konnte. Später konstruierte er auch Taschenuhren mit Spiralfedern und Unruh. Christiaan Huygens veröffentlichte 1673 in seiner Abhandlung Horologium Oscillatorium eine ganggenaue Pendeluhr mit einem Zykloidenpendel, bei dem er sich die Tatsache zunutze machte, dass die Evolute der Zykloide selber wieder eine Zykloide ist. Der Vorteil der Ganggenauigkeit wird jedoch durch die erhöhte Reibung wettgemacht. In seiner letzten wissenschaftlichen Abhandlung 1690 formulierte Huygens den Gedanken, dass es noch viele andere Sonnen und Planeten im Universum geben könnte, und spekulierte bereits über außerirdisches Leben. Huygens entdeckte die Beziehungen zwischen Schallgeschwindigkeit, Länge und Tonhöhe einer Pfeife. Er beschäftigte sich intensiv mit der mitteltönigen Stimmung und berechnete 1691 die Teilung der Oktave in 31 gleiche Stufen, um den Fehler des pythagoreischen Kommas im Tonsystem der Musik zu beheben. Die Ausarbeitung und Verbesserung des snelliusschen Ansatzes leistete Christiaan Huygens in seiner Arbeit De circuli magnitudine inventa, in der er auch den Beweis der von Snellius aufgestellten Sätze erbrachte. Auf rein elementargeometrischem Weg gelang Huygens eine so gute Eingrenzung der zwischen Vieleck und Kreis liegenden Fläche, dass er bei entsprechender Seitenzahl der Polygone die Kreiszahl auf mindestens dreimal soviel Stellen genau erhielt wie Archimedes mit seinem Verfahren. |
| Thomas
Hobbes (5. April 1588 - 4.
Dezember 1679) war ein englischer Mathematiker,
Staatstheoretiker und Philosoph, der durch sein Hauptwerk
Leviathan, in dem er eine Theorie des Absolutismus
entwickelte, bekannt geworden ist. Er gilt als Begründer
des aufgeklärten Absolutismus. Des Weiteren ist er neben
John Locke und Jean-Jacques Rousseau einer der
bedeutendsten Vertragstheoretiker. Insbesondere in seinem Werk De Corpore, dem ersten Teil der Trilogie elementa philosophiae, von 1655 entwickelt Hobbes zentrale Thesen zu naturwissenschaftlichen Fragen. Ausgehend von einer materialistischen Grundhaltung und dem – exemplarisch durch René Descartes vertretenen – mechanistischen Denken seiner Zeit schreibt er allein den Körpern und deren Bewegung Wirklichkeit zu. Dabei entsteht keine Bewegung aus sich selbst heraus, sondern ist Folge einer anderen Bewegung. Der Bewegung unterliegen nur Körper; sie können ausschließlich durch andere Körper bewegt werden. Auf der Grundlage dieser Körper-Lehren entwickelt Hobbes mitunter erstaunlich modern anmutende Theorien etwa zum Phänomen des Lichts, das sich seiner Ansicht gemäß in materieartigen Impulsen bewegt, und veröffentlichte auch ein Werk über Optik. Auch beschäftigte er sich vor diesem Hintergrund mit der Natur des Vakuums. Dazu kommen einige Werke über Mathematik; Begeistern konnte sich Hobbes insbesondere auch für Euklidische Geometrie, die ihm als Vorbild für jegliche exakte Wissenschaft galt und deren Grundsätze er entsprechend dem mos geometricus auch auf seine Philosophie übertragen wollte. Gleichwohl galt Hobbes auf diesem Gebiet vielfach als Dilettant; um ihn auch als Philosophen zu diskreditieren, setzte die Kirche Mathematiker ein, um seine Bemühungen der Lächerlichkeit preiszugeben. Außerdem ist er ein prominentes Beispiel für einen Amateurmathematiker, der die Quadratur des Kreises gefunden zu haben glaubte. Seine 1665 in seinem Werk De corpore veröffentlichte Lösung – in Wirklichkeit eine Näherungskonstruktion – wurde von John Wallis noch im selben Jahr zurückgewiesen. In der Folgezeit entspann sich zwischen den beiden eine in scharfem Tonfall vorgetragene Auseinandersetzung, die erst mit Hobbes' Tod im Jahr 1679 endete. |
| Adam
Adamandy Kochanski (5. August 1631 -
17. Mai 1700) war ein polnischer Mathematiker. Kochanski
besuchte ein Gymnasium in Thorn und studierte ab Jahr
1652 in Vilnius Philosophie, Mathematik, Physik und
Theologie. Später unterrichtete er diese Fächer u.a. in
Florenz, Prag, Breslau, Mainz und Würzburg. Im Jahre
1677 wurde er in Warschau zum Hofmathematiker und
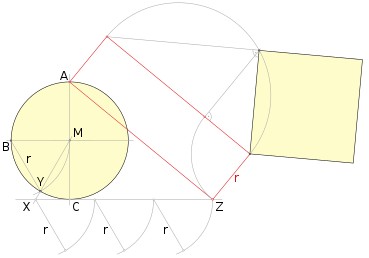
Bibliothekar des Königs Johann III. Sobieski. Kochanski hat sich mit den Problemen der Konstruktion der mechanischen Uhren beschäftigt. Bekannt ist vor allem seine 1685 entwickelte sogenannte Näherungskonstruktion von Kochanski, mit der ein Quadrat konstruiert werden kann, das nahezu flächengleich zu einem gegebenen Kreis ist, also eine näherungsweise Lösung der Quadratur des Kreises darstellt. Siehe dazu: Nährungskonstruktion - Kochanski |
| Um 1700 herum war Jacob Marcelis der Meinung, daß es ihm gelungen sei, den Kreis zu quadrieren, und damit den exakten Wert für π zu bestimmen. Diesen gab er wie folgt an: |
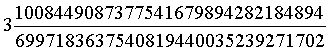 |
| Berichte über ein wachsendes
Aufkommen an Amateurarbeiten ab dem 18. und 19.
Jahrhundert und Beispiele zum Thema finden sich bei
Jean-Étienne Montucla, Johann Heinrich Lambert und
Augustus de Morgan. In der Regel handelte es sich um
Verfahren, bei denen das Problem mechanisch, numerisch
oder durch eine geometrische Näherungskonstruktion
„exakt“ gelöst wurde. Derartige Arbeiten wurden in einer so großen Zahl an Mathematiker oder wissenschaftliche Institutionen herangetragen, dass sich zum Beispiel die Pariser Akademie der Wissenschaften 1775 genötigt sah, die weitere Untersuchung von vorgeblichen Lösungen der Kreisquadratur offiziell abzulehnen: Die Akademie hat dieses Jahr die Entscheidung getroffen, in Zukunft weder die Lösungen der mathematischen Probleme betreffend die Verdoppelung des Würfels, die Dreiteilung des Winkels sowie die Quadratur des Kreises, noch jedwede Maschine mit dem Anspruch eines "Perpetuum mobile" zu untersuchen.“ |