Copyright © Klaus Piontzik
| Dem Schalenaufbau der Erde
liegt ein Schwingungsspektrum zugrunde Dem Schichtenaufbau der Atmosphäre liegt ein Schwingungsspektrum zugrunde Beide Schwingungsspektren sind Teile des gesamten magnetischen Schwingungsspektrums der Erde. |
| Die Erde stellt, über das Magnetfeld, mit ihrem Inneren und der Atmosphäre eine schwingungsmässige Einheit dar. |
| Fasst man die Distanzen l' aus der Distanztabelle als Wellenlänge der zugehörigen Hülle bzw. Schwingungsschicht auf, dann lassen sich, wie gesehen, allen Distanzen entsprechende Frequenzen zuordnen. Dies gilt auch für die gefundenen Mittelwerte der Extremalschichten. |
| Abstand | Frequenz | Höhe |
| km | Hz | km |
| 6990,732 | 10,720 | 619,732 |
| 6976,920 | 10,741 | 605,920 |
| 6938,627 | 10,801 | 567,627 |
| 6887,079 | 10,882 | 516,079 |
| 6862,834 | 10,920 | 491,835 |
| 6843,795 | 10,950 | 472,796 |
| 6804,379 | 11,014 | 433,380 |
| 6775,855 | 11,060 | 404,855 |
| 6756,334 | 11,092 | 385,335 |
| 6742,948 | 11,114 | 371,949 |
| 6730,327 | 11,135 | 359,327 |
| 6688,747 | 11,204 | 317,748 |
| 6656,928 | 11,258 | 285,928 |
| 6636,025 | 11,293 | 265,025 |
| 6613,459 | 11,332 | 242,459 |
| 6593,773 | 11,366 | 222,774 |
| 6560,285 | 11,424 | 189,285 |
| 6539,935 | 11,459 | 168,935 |
| 6509,032 | 11,514 | 138,032 |
| 6480,640 | 11,564 | 109,641 |
| 6458,118 | 11,604 | 87,118 |
| 6437,634 | 11,641 | 66,635 |
| 6400,349 | 11,709 | 29,349 |
| Für alle Schichtfrequenzen der Atmosphäre gilt dann: |
| Da bestimmte Schichten der Atmosphäre mit Freuqenzen, also elektromagnetischen Aktivitäten verbunden sind, sollte es also nicht verwundern das Ereignisse bzw. Prozesse in bestimmten Höhen (also Wetterbildung) mit Frequenzen bzw. elektromagnetischen Signalen verbunden sind. Der Nachweis der Sferics bestätigt hier ja das Modell. |
| Fasst man die Distanzen l' aus der Distanztabelle als Wellenlänge der zugehörigen Hülle bzw. Schwingungsschicht auf, dann lassen sich, wie in Kapitel 15 und 16.1 gesehen, auch allen Distanzen innerhalb der Erde aus Kapitel 13 entsprechende Frequenzen zuordnen. |
| Abstand | Frequenz | Tiefe |
| km | Hz | km |
| 6355,76 | 11,79 | 15 |
| 6286,11 | 11,92 | 85 |
| 6191,29 | 12,10 | 180 |
| 6039,09 | 12,16 | 332 |
| 5982,18 | 12,52 | 389 |
| 5916,98 | 12,66 | 454 |
| 5766,16 | 12,99 | 605 |
| 5710,59 | 13,12 | 660 |
| 5667,58 | 13,22 | 703 |
| 5588,12 | 13,41 | 783 |
| 5359,12 | 13,98 | 1012 |
| 5258,39 | 14,25 | 1113 |
| 5105,49 | 14,68 | 1266 |
| 5022,45 | 14,92 | 1349 |
| 4953,86 | 15,13 | 1417 |
| 4914,98 | 15,25 | 1456 |
| 4855,23 | 15,43 | 1516 |
| 4781,63 | 15,67 | 1589 |
| 4678,69 | 16,02 | 1692 |
| 4483,91 | 16,71 | 1887 |
| 4357,42 | 17,20 | 2014 |
| 4177,23 | 17,94 | 2194 |
| 4026,54 | 18,61 | 2344 |
| 3937,52 | 19,03 | 2433 |
| 3851,37 | 19,46 | 2520 |
| 3710,71 | 20,19 | 2660 |
| 3589,32 | 20,88 | 2782 |
| 3508,23 | 21,36 | 2863 |
| 3410,02 | 21,98 | 2961 |
| 3374,53 | 22,21 | 2996 |
| 3203,35 | 23,39 | 3168 |
| 3045,35 | 24,61 | 3326 |
| 2971,18 | 25,22 | 3400 |
| 2899,27 | 25,85 | 3472 |
| 2690,05 | 27,86 | 3681 |
| 2587,64 | 28,96 | 3783 |
| 2485,39 | 30,15 | 3886 |
| 2351,41 | 31,87 | 4020 |
| 2162,10 | 34,66 | 4209 |
| 1989,48 | 37,67 | 4382 |
| 1897,28 | 39,50 | 4474 |
| 1735,07 | 43,19 | 4636 |
| 1632,65 | 45,90 | 4738 |
| 1464,59 | 51,17 | 4906 |
| 1304,91 | 57,43 | 5066 |
| 1137,12 | 65,91 | 5234 |
| 1071,01 | 69,98 | 5300 |
| 878,32 | 85,33 | 5493 |
| 776,94 | 96,46 | 5594 |
| 525,42 | 142,64 | 5846 |
| 423,39 | 177,02 | 5948 |
| 299,08 | 250,59 | 6072 |
| Für alle Schichtfrequenzen des Erdinneren gilt dann: |
| Da bestimmte Schichten des Erdinneren mit Freuqenzen, also elektromagnetischen Aktivitäten verbunden sind, sollte es also nicht verwundern das Ereignisse bzw. Prozesse in bestimmten Tiefen (also Erdbeben, Plattentektonik) mit Frequenzen bzw. elektromagnetischen Signalen behaftet sind. |
| Insgesamt ergibt sich aus der vorhergehenden Betrachtung: |
| Die Grenzfrequenz fErde stellt praktisch den Oberflächenwert der Erde dar. Da alle Lebewesen der Erde in einer Zone von etwa 10 Km tiefer oder höher auftreten, lässt sich folgende Aussage tätigen |
| Alles Leben auf der Erde ist an
einen Frequenzbereich von 11,7 - 11,8 Hz angepasst. Aus den Betrachtungen des vorhergehenden Kapitels folgt auch das wir an die Bereiche 23,4-23,6 Hz sowie 46,8-47,2 Hz angepasst sind. |
| In Anbetracht der Ergebnisse aus Kapitel 15.5 gelten auch die Frequenzbereiche, die sich an der Schumann-Frequenz orientieren, die also um eine Quinte verschoben sind. |
| Alles Leben auf der Erde ist an
einen Frequenzbereich von 11,7 - 11,8 Hz angepasst. Alles Leben auf der Erde ist ebenso an die Frequenzbereiche von 7,8-7,9 Hz sowie 15,6-15,7 Hz und 31,2-31,5 Hz angepasst |
| Mit Kapitel 15.5 lässt sich dann folgende Definition aufstellen: |
| Die von der Erdfrequenz und der
Schumann-Frequenz erzeugten gemeinsamen Frequenzen werden als biologische Frequenzen bezeichnet |
| Ab Mitte der 70er Jahre machten William Ross Adey und S.M.
Bawin Versuche mit Gehirngewebe von Hühnern und Katzen.
Sie bestrahlten das Gewebe mit modulierten VHF-Feldern. (siehe „Effects of modulated VHF fields on the central nervous system“ in „Ann N Y Acad Sci 247“ 1975 von Bawin, Kaczmarek und Adey / „Sensitivity of calcium binding in cerebral tissue to weak environ-mental electric fields oscillating at low frequency“ 1976 in „Proc. Natl. Acad. Sci. 73“ von Bawin und Adey / „Ionic factors in release of 45Ca2+ from chicken cerebral tissue by electromagnetic fields“ in „Proc Natl Acad Sci USA. 75“ 1978 von Bawin, Adey und Sabbot / „Models of long-range order in cerebral macromolecules: Effects of sub-ELF and of modulated VHF and UHF fields“ 1979 in „Radio Sci 14“ von Sheppard, Bawin und Adey / „Frequency and power windowing in tissue interactions with weak electromagnetic fields“ 1980 in „Proc. IEEE 68“ von Adey / „Tissue interactions with non-ionizing electromagnetic fields“ 1981 in „Physiol. Rev. 61“ von Adey / „Effects of weak amplitude-modulated microwave fields on calcium efflux from awake cat cerebral cortex“ in „Bioelectromagnetics 3“ 1982 von Adey, Bawin und Lawrence) Bei ihren Untersuchungen fanden Adey und Bawin einen schmalen Intensitäts- und Frequenzbereich, in welchem die behandelten Zellen reagierten. Außerhalb dieser Bereiche erfolgte jedoch keine bzw. nur minimale Reaktion. Der experimentell ermittelte Frequenzbereich wird inzwischen als Adey-Fenster bezeichnet. |
|
| Abbildung 16.1 - Das Adey-Fenster |
| In Abbildung 16.1 ist im oberen (rechts mit A
gekennzeichnetem) Bereich ein Versuch von Bawin aus dem
Jahr 1975 zu sehen. Dabei wurde eine Frequenz von 147 MHz
mit einer ELF-Amplitudenmodulation benutzt. Als Reaktion
auf die Bestrahlung wurde der Ca-Ionen-Efflux der Zellen
gemessen. Im unteren Teil (rechts mit B gekennzeichnet) ist ein Versuch von Adey und Bawin aus dem Jahr 1976 dargestellt. Mit gleichem Gewebetyp aber mit einem ELF-Feld das in der Frequenz variabel war. Für Teil A der Abbildung 16.1 gilt: In einem Bereich von 3 Hz bis etwa 25 Hz ist eine prägnante Reaktion zu erkennen. Deutlich ist zu sehen, dass von 6 Hz bis 20 Hz ein Maximum an Reaktion gegeben ist. |
| Ein Vergleich mit den bisher ermittelten
Frequenzbereichen aus Kapitel 16.3 ergibt, dass die
Bereich 7,8-7,9 Hz sowie 11,7-11,8 Hz und 15,6-15,7 Hz im
Maximalbereich des Adey-Fensters liegen, wenn man das
Adey-Fenster als Kontinuum auffasst. Die Gleichung 3 aus Kapitel 6 liefert die Erdfrequenzen: für n=1 ergab sich 11,75 Hz, für n=2 ergab sich16,62 Hz und für n=3 ergab sich 23,5 Hz (siehe Tabelle 20). Auch diese Frequenzen liegen gut im Adey-Fenster, wenn man das Adey-Fenster als Kontinuum auffasst. |
| Betrachtet man das Adey-Fenster nicht
als Kontinuum, sondern nimmt die in der Abbildung 16.1
angegebenen diskreten Frequenzen, so
erhält man die folgende Reihe (in Hz): 3 – 6 – 9 – 16 – 20 – 25 – 35 Wobei um jede Frequenz ein Bereich von ±0,8 Hz Toleranz besteht. |
| Aus der Gleichung in Kapitel 15.5 folgte die Tabelle
der Frequenzen, die Erdfrequenz und Schumann-Frequenz
gemeinsam besitzen. Dabei tritt fo/3=fs/2=3,9307 Hz als
erste kleinste natürliche Frequenz auf, die Erdfrequenz
und Schumann-Frequenz gemeinsam besitzen. Daraus ergibt sich eine Reihe von Frequenzen, die alle ein Vielfaches der Grundfrequenz 3,93 Hz sind (erste Spalte in Tab.45). Die ersten neun Frequenzen lauten: 3,9307 - 7,8613 - 11,792 - 15,7227 - 19,6533 - 23,584 - 27,5147 - 31,4453 - 35,376 Ein Teil dieser Frequenzen stimmt gut mit den Frequenzen des Adey-Fensters überein. Werden die Werte dieser Reihe halbiert ergibt sich: 1,9653 - 3,9307 - 5,896 - 7,8613 - 9,8267 - 11,792 - 13,7574 - 15,7227 - 17,688 Siebt man nun von allen vorhandenen Frequenzen diejenigen heraus, die auch in der Abbildung 16.1 (Teil A) enthalten sind, ergibt sich folgendes Frequenzspektrum für das Adey-Fenster: 3,9307 - 5,896 - 9,8267 - 15,7227 - 19,6533 - 23,584 - 35,376 Das entspricht dann den Frequenzen des Adey-Fensters. Man kann diese Frequenzen auch als ganzrationale Vielfache der Erdfrequenz und auch der Schumann-Frequenz darstellen. Das ergibt die folgende Tabelle: |
Frequenzen des Adey-Fensters 1
| 3,9307 | 5,896 | 9,8267 | 15,7227 | 19,6533 | 23,584 | 35,376 |
| 1/2 fS | 3/4 fS | 5/4 fS | 2 fS | 5/2 fS | 3 fS | 9/2 fS |
| 1/3 f0 | 1/2 f0 | 5/6 f0 | 4/3 f0 | 5/3 f0 | 2 f0 | 3 f0 |
| Die
Frequenzen des Adey-Fensters stehen in harmonikalen
Verhältnissen zur Erdfrequenz bzw. zur Schumann-Frequenz. |
| Die Kongruenz zwischen Adey-Fenster und Erdfrequenzen liefert also eine Bestätigung des bisher abgeleiteten Modells bzw. der These, dass alles Leben auf diesem Planeten an bestimmte Frequenzbereiche angepasst ist. Die ausführliche Abhandlung dazu findet im Kapitel 18 statt. |
| Bei Bildung der halben Frequenzen in Kapitel 16.4
fiel als kleinste Frequenz fm=1,9653
Hz an. Es gilt: fm = 1/4 fs = 1/6 fo Vergleicht man fm mit den Frequenzen des Adey-Fensters, so sind alle auftretenden Adey-Frequenzen Vielfache von 1,9653 Hz. Berücksichtigt man dies, so lassen sich die Frequenzen wie folgt darstellen: |
Frequenzen des Adey-Fensters 2
| 3,9307 | 5,896 | 9,8267 | 15,7227 | 19,6533 | 23,584 | 35,376 |
| 2 fm | 3 fm | 5 fm | 8 fm | 10 fm | 12 fm | 18 fm |
| Es entsteht so die Zahlenfolge: 2 – 3 – 5
– 8 – 10– 12 – 18 Und das entspricht etwa der, aus der Mathematik bekannten Fibonacci-Folge mit: 2 – 3 – 5 – 8 – 13 – 21 Dass die Fibonacci-Folge hier eine Rolle spielt, kann man aus den Frequenzen des Adey-Fensters auch direkt ableiten: Die Adey-Frequenzfolge: 3 – 6 – 9 – 16 – 20 – 25 – 35 halbieren: 1,5 – 3 – 4,5 – 8 – 10 – 12,5 – 17,5 und runden: 2 – 3 – 5 – 8 – 10 – 13 – 18 |
| Die Fibonacci-Folge spielt immer da
eine Rolle, wo Proportionen mit dem goldenen
Schnitt zu finden sind. Die Fibonacci-Folge
kommt daher auch in der Natur vor, wie bei
spiralförmigem Wuchs von Pflanzen oder auch in der
Struktur von Samenkörnern in Blütenständen
(Sonnenblume). Gleichfalls taucht die Fibonacci-Folge in
der Größe der Populationen auf, z.B. bei Kaninchen und
auch Bienen. Es sollte also nicht verwundern, diese Zahlenfolge auch im Zusammenhang mit den Frequenzen des Adey Fensters zu finden. |
Tab.52: Frequenzen des Adey-Fensters als Fibonacci-Folge
| 3,9307 | 5,896 | 9,8267 | 15,7227 | 25,549 |
| 2 fm | 3 fm | 5 fm | 8 fm | 13 fm |
| Im Buch wird noch die Gleichung nach Binet für die Fibonacci-Folge des Adey-Fensters angegeben. |
| Zur Fibonacci-Folge und auch zur Gleichung von Binet
ist im Internet in der „Wikipedia“ eine gute
Zusammenstellung und Darstellung zu finden. Durch die Auseinandersetzung mit den Frequenzen des Adey-Fensters und der Fibonacci-Folge bedingt, gelang die Aufstellung einer zweiten Gleichung mit der sich die besprochenen Frequenzen ableiten lassen. Ohne weitere Ableitung wird hier nur das Ergebnis bekannt gegeben: |
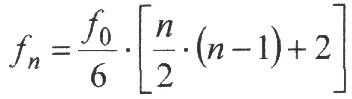 |
| Daraus ergibt sich diese Frequenz-Folge: 3,9307 - 5,896 - 9,8267 - 15,7227 - 23,584 - 33,411 Was die Frequenzen des Adey Fensters recht gut wiedergibt. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |