Copyright © Klaus Piontzik
| Schaut man sich die Distanzen näher an, dann erkennt man das sie alle Vielfache des Radius R=6355758,426 m = Lo bilden. Dies ist der Grundhüllenradius. Also lassen sich die Distanzwerte auch so darstellen: |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| n | m | ||||||||
| 1 | 1 | Lo | 3Lo | 5Lo | 7Lo | 9Lo | 11Lo | 13Lo | 15Lo |
| Fasst man die Distanzen l' aus der Distanztabelle als Wellenlänge der zugehörigen Hülle bzw. Schwingungsschicht auf, dann lassen sich allen Distanzen auch Frequenzen zuordnen. |
| FALL 1 |
| Eine Möglichkeit besteht darin sich an der Abbildung 6.2 zu orientieren. Das bedeutet der doppelte Durchmesser entspricht der Wellenlänge. Es gilt dann λ = 4R = 4l' und: |
 |
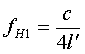| Aus der Distanztabelle werden, für die folgende Betrachtungen, die Distanzwerte für n=1 benutzt. |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| n | m | |||||||||
| 1 | 1 | 11,79 | 3,93 | 2,358 | 1,68 | 1,31 | 1,07 | 0,907 | 0,786 | Hz |
| 6355,76 | 19067,28 | 31778,79 | 44490,31 | 57201,83 | 69913,34 | 82624,86 | 95336,38 | Km |
| Zu beachten ist hier das für k=2 die halbe Schumann-Frequenz entsteht. |
| FALL 2 |
| Eine weitere Möglichkeit besteht darin den gesamten Durchmesser der zugehörigen Hülle bzw. Schwingungsschicht als Wellenlänge zu nehmen. Also λ = 2R = 2l' und: |
 |
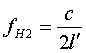| Aus der Distanztabelle werden wieder die Distanzwerte für n=1 benutzt. |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| n | m | |||||||||
| 1 | 1 | 23,584 | 7,861 | 4,716 | 3,369 | 2,62 | 2,143 | 1,814 | 1,572 | Hz |
| 6355,76 | 19067,28 | 31778,79 | 44490,31 | 57201,83 | 69913,34 | 82624,86 | 95336,38 | Km |
| Zu beachten ist hier das für k=2 die Schumann-Frequenz entsteht. Das bedeutet aber auch das die Schuhmann-Frequenz im Spektrum der erdmagnetischen Frequenzen bereits enthalten ist. Alle auftretenden Frequenzen sind quasi Verdopplungen der bereits gefundenen Grundfrequenzen stellen also Oberwellen dar. |
| FALL 3 |
| Zum Abschluss hier noch die Möglichkeit den Radius der zugehörigen Hülle bzw. Schwingungsschicht als Wellenlänge zu interpretieren. Also λ = R = l' und: |
 |
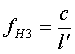| Aus der Distanztabelle werden wieder die Distanzwerte für n=1 benutzt. |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| n | m | |||||||||
| 1 | 1 | 47,17 | 15,72 | 9,43 | 6,74 | 5,24 | 4,29 | 3,63 | 3,14 | Hz |
| 6355,76 | 19067,28 | 31778,79 | 44490,31 | 57201,83 | 69913,34 | 82624,86 | 95336,38 | Km |
| Alle auftretenden Frequenzen sind quasi Vervierfachungen der bereits gefundenen Grundfrequenzen, stellen also lediglich Oberwellen dar. |
| Insgesamt lassen sich die Distanz- und Frequenzwerte für n=1 dann folgendermassen darstellen: |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| n | m | ||||||||
| 1 | 1 | 3/2fS | 1/2fS | 3/10 fS | 3/14 fS | 1/6 fS | 3/22 fS | 3/26 fS | 1/10 fS |
| 1/f0 | 1/3f0 | 1/5f0 | 1/7f0 | 1/9f0 | 1/11f0 | 1/13f0 | 1/15f0 | ||
| Lo | 3Lo | 5Lo | 7Lo | 9Lo | 11Lo | 13Lo | 15Lo |
| Die Konsequenz ist, dass alle auftretenden Frequenzen in Fall 1 als gebrochen rationale Vielfache bestimmter Grundfrequenzen darstellbar sind. |
| Im Buch wird die Tabelle der Extremalschichten aus Kapitel 12.2 durch die geschilderte Zuordnung (Fall 1) zu einer Frequenztabelle transformiert. |
| Schaut man sich die Frequenzen näher an, dann lässt
sich daraus ein Zusammenhang zwischen Erdfrequenz und
Schumann-Frequenz ableiten. Am einfachsten gelingt dies mit den Frequenzen fH2. Es existiert nämlich eine gemeinsame Teilungsfrequenz. |
| Für k=1 und k=2 existiert ein gemeinsame
Teilungsfrequenz mit: 23,584 = 3 * 7,861 23,584 = 2 * 11,792 Die Frequenz 7,861 Hz = fS entspricht der Schumann-Freuqenz Dann lässt sich die Frequenz für k=1 andererseits so zerlegen: |
| 23,584 Hz =3fS = 2f0 |
| Der allgemeine Zusammenhang lautet (siehe Kapitel 15.2 - Fall2): |
|
| Und daraus direkt ableitbar: |
 |
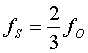| Die Schumann-Frequenz ist im Spektrum der Erdfrequenzen bereits enthalten |
| Aus der Gleichung für fH2 ist auch direkt ableitbar: |
 |
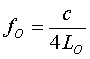| Weiterhin direkt ableitbar: |
 |
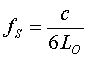| Der Grundhüllenradius ist nur ein wenig kleiner als Pol- bzw. Äquatorradius. daher stellt sich hier die Frage, welche Grössen fS besitzt, wenn der Hüllenradius durch RA bzw. RP ersetzt wird |
| Die Daten des Geodätischen
Referenzsystems WGS84 lauten: Polradius: RP= 6356752 m Äquatorradius: RA= 6378137 m Mit c = 299792458 m/s als Lichtgeschwindigkeit ergibt sich für die einzelnen Frequenzen: |
||
| Für die Erdfrequenzen: | ||
| Für den Polradius |  |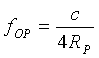
= 11,7899 Hz |
| Für den Äquatorradius |  |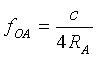
= 11,7503 Hz |
| Für die Schumann-Frequenzen: | ||
| Für den Polradius |  |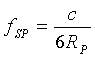
= 7,8602 Hz |
| Für den Äquatorradius |  |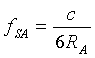
= 7,8339 Hz |
| Bemerkenswert ist hier noch der Umstand das die Schumann-Frequenz ja historischerweise aus einer Hohlraumresonator-Betrachtung gewonnen wird (siehe dazu Kapitel 7.1). Die gleichzeitige Ableitung aus der Erdfrequenz, also letztlich aus den Radien der Erde, zeigt das die Abmessungen dieses Planeten und die darauf erzeugten Frequenzen in einem engen Zusammenhang stehen. |
| Nimmt na den, in den geophysikalischen Wissenschaften üblichen, mittleren Radius von 6371 Km, erhält man für fS einen Wert von 47,0558 Hz. Das liegt nahe bei 47 Hz. |
| Rechnet man mit 47 Hz zurück, ergibt sich der Radius zu 6378,563 Km. Das ist etwa 400 Meter grösser als der Äquatorradius. Näherungsweise kann man also sagen: |
| 47 Hz =6fS = 4f0 |
| Daraus ergibt sich: |
| fS = 47:6 Hz = 7,8333... Hz |
| f0 = 47:4 Hz = 11,75 Hz |
| Dies lässt sich als gute Näherung für die Äquatorradius-Frequenzen benutzen. |
| Aus Gleichung aus Kapitel 15.3 lässt sich noch ein
allgemeiner Zusammenhang zwischen Erdfrequenz und
Schumann-Frequenz ableiten. Die Beziehung f0/3 = fS/2 bleibt ja auch dann erhalten, wenn man die Gleichung mit einer ganzrationalen Zahl, also einem Bruch, multipliziert. Damit ergibt sich allgemein: |
 |
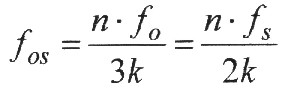| n und k sind dabei Elemente der natürlichen Zahlen (1, 2, 3, 4...) |
| Durch die Gleichung entsteht ein komplettes Spektrum
an gemeinsamen Frequenzen fos, so dass die
Erdfrequenz und die Schumann-Frequenz miteinander in
einem funktionalen Zusammenhang stehen. Systematisches Einsetzen der Parameter n und k in die Gleichung führt zu einer Tabelle, in der dann alle gemeinsamen Frequenzen enthalten sind Die Berechnung der Tabellenwerte erfolgt über die korrigierte Grundfrequenz aus Kapitel 11.2. Es wird ein gerundeter Wert von fo = 11,792 Hz benutzt. |
| gemeinsame Frequenzen für n<17, k<9 |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| n | |||||||||
| 1 | 3,9307 | 1,9653 | 1,3102 | 0,9827 | 0,7861 | 0,6551 | 0,5615 | 0,4913 | Hz |
| 2 | 7,8613 | 3,9307 | 2,6204 | 1,9653 | 1,5723 | 1,3102 | 1,123 | 0,9827 | Hz |
| 3 | 11,792 | 5,896 | 3,9307 | 2,948 | 2,3584 | 1,9653 | 1,6846 | 1,474 | Hz |
| 4 | 15,7227 | 7,861 | 5,2409 | 3,9307 | 3,1445 | 2,6204 | 2,2461 | 1,9653 | Hz |
| 5 | 19,6533 | 9,8267 | 6,5511 | 4,9133 | 3,9307 | 3,2756 | 2,8076 | 2,4567 | Hz |
| 6 | 23,584 | 11,792 | 7,8613 | 5,896 | 4,7168 | 3,9307 | 3,3691 | 2,948 | Hz |
| 7 | 27,5147 | 13,7573 | 9,1716 | 6,8787 | 5,503 | 4,5858 | 3,9307 | 3,4393 | Hz |
| 8 | 31,4453 | 15,7227 | 10,4818 | 7,8613 | 6,2891 | 5,2409 | 4,4922 | 3,9307 | Hz |
| 9 | 35,376 | 17,688 | 11,792 | 8,844 | 7,0752 | 5,896 | 5,0537 | 4,422 | Hz |
| 10 | 39,3067 | 19,6533 | 13,1022 | 9,8267 | 7,8613 | 6,5511 | 5,6152 | 4,9133 | Hz |
| 11 | 43,2373 | 21,6187 | 14,4124 | 10,8093 | 8,6475 | 7,2062 | 6,1768 | 5,4047 | Hz |
| 12 | 47,168 | 23,584 | 15,7227 | 11,792 | 9,4336 | 7,8613 | 6,7383 | 5,896 | Hz |
| 13 | 51,0987 | 25,5493 | 17,0329 | 12,7747 | 10,2197 | 8,5164 | 7,2998 | 6,3873 | Hz |
| 14 | 55,0293 | 27,5147 | 18,3431 | 13,7573 | 11,0059 | 9,1716 | 7,8613 | 6,8787 | Hz |
| 15 | 58,96 | 29,48 | 19,6533 | 14,74 | 11,792 | 9,8267 | 8,4229 | 7,37 | Hz |
| 16 | 62,8907 | 31,4453 | 20,9636 | 15,7227 | 12,5781 | 10,4818 | 8,9844 | 7,8613 | Hz |
| Ein weiterer Zusammenhang aus der Gleichung von Kapitel 15.5 ergibt sich wenn größere n, also höhere Frequenzen, betrachtet werden: |
| gemeinsame Frequenzen für 1055<n<12673, k<9 |
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| n | |||||||||
| 1056 | 4150,784 | 2075,392 | 1383,595 | 1037,696 | 830,157 | 691,797 | 592,969 | 518,848 | Hz |
| 1584 | 6226,176 | 3113,088 | 2075,392 | 1556,544 | 1245,235 | 1037,696 | 889,454 | 778,272 | Hz |
| 2112 | 8301,568 | 4150,784 | 2767,189 | 2075,392 | 1660,314 | 1383,595 | 1185,938 | 1037,696 | Hz |
| 2640 | 10376,96 | 5188,48 | 3458,987 | 2594,24 | 2075,392 | 1729,493 | 1482,423 | 1297,12 | Hz |
| 3168 | 12452,35 | 6226,176 | 4150,784 | 3113,088 | 2490,47 | 2075,392 | 1778,907 | 1556,544 | Hz |
| 7128 | 28017,79 | 14008,89 | 9339,264 | 7004,448 | 5603,558 | 4669,632 | 4002,542 | 3502,224 | Hz |
| 12672 | 49809,41 | 24904,7 | 16603,14 | 12452,35 | 9961,882 | 8301,568 | 7115,63 | 6226,176 | Hz |
| Die spektralen Maxima der Sfericfrequenzen befinden sich in sehr schmalbandigen Bereichen die allgemein, wie folgt, angegeben werden (siehe „Sferics“ von Hans Baumer S.285): |
| 4150,84 Hz - 6226,26 Hz - 8301,26 Hz - 10377,10 Hz - 12452,52 Hz - 28018,17 Hz - 49810,08 Hz |
| Der Vergleich des Sferic-Spektrums mit den
Tabellenwerten liefert eine gute Übereinstimmung der
Werte. Über das ganze Spektrum gesehen liegt der
maximale Fehler unter 0,7 Hz. In seinem Buch „Die kosmische Oktave“ (Seite 39) stellt Cousto einen Zu-sammenhang zwischen Sfericfrequenz und Sterntag her. Der Vergleich mit der Erdrotation liefert eine minimale Differenz von etwa 3 Hz und vergrößert sich bei zunehmender Frequenz bis zu einem Maximalwert von etwa 36 Hz. Die zunehmende Differenz zeigt deutlich das die Frequenzberechnung über den Sterntag nur als Näherungswert tauglich ist. Wie durch die Gleichung aus Kapitel 15.5 und die erzeugte Tabelle für 1055 < n < 12673 gezeigt worden ist sind die Sfericfrequenzen, mit hinreichender Genauigkeit, im Spektrum der gemeinsamen Erdfrequenzen und Schumann-Frequenzen enthalten. |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
