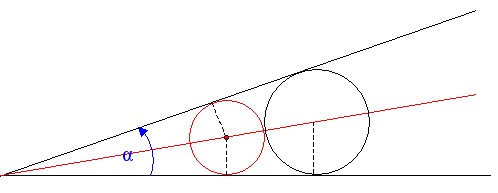
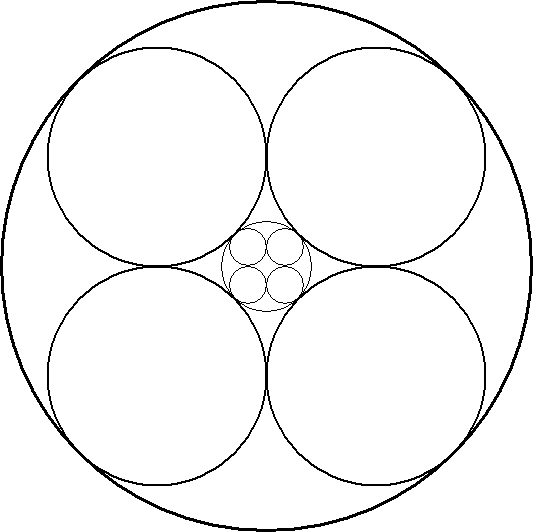
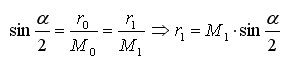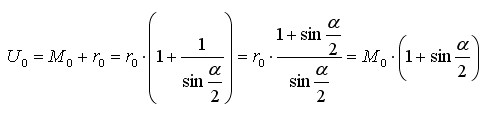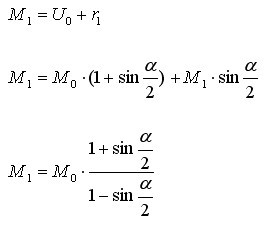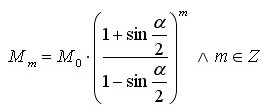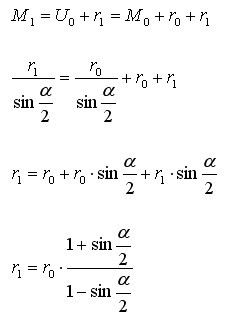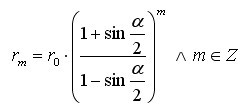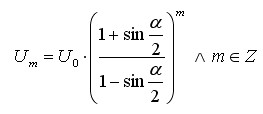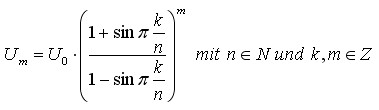| Ausgang ist wieder ein Koordinatensystems,
dass als Grundlage für den Winkel alpha
dient. In diesem Winkel liegt ein Kreis mit dem Radius r0.
Gesucht ist nun der nächst größere Kreis mit dem
Radius r1
der in den Winkel passt und sowohl den Ursprungskreis als
auch die Winkelseiten tangiert.
Aufgrund der Proportionalität in den auftretenden Dreiecken gilt:
mit dem Umkreis U0:
Für den neuen Mittelpunktsabstand M1 gilt:
Dann gilt allgemein für die m-te Wachstumsstufe der Mittelpunktsabstände:
Für den neuen Mittelpunktsabstand M1 lässt sich auch schreiben:
Dann gilt allgemein für die m-te Wachstumsstufe der Radien:
Dann gilt allgemein auch für die m-te Wachstumsstufe der Umkreise:
Setzt man alle Größen für die Winkel ein, so ergibt sich die allgemeine Gleichung für die Umkreise von Vielkreis-Systemen:
|