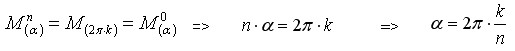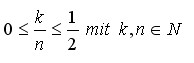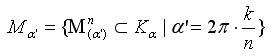ABLEITUNG PRIMÄRE VIELKREIS-SYSTEME

K_alpha sei die Menge aller Drehungen mit:

Dreht man einen Kreis bzw. den zugehörigen Vektor n-mal und schließt sich die Kreisfigur nach k Umdrehungen wieder, dann gilt:

Es gelte: k,n sind teilerfremd und:

dann ist

die Menge der primären Vielkreis-Systeme

Vielkreis-Systeme lassen sich auch als Datenpaar notieren:

(1;1) (2;1) (3;1) (4;1) (5;1) (6;1) (7;1) (8;1) (9;1) (10;1) (11;1) (12;1) (13;1) (14;1) (15;1) (16;1)

Für k=2 ergeben sich folgende Vielkreissysteme:

(5;2) (7;2) (9;2) (11;2) (13;2) (15;2)

Für k=3 ergeben sich foldende Vielkreissysteme:

(7;3) (8;3) (10;3) (11;3) (13;3) (14;3) (16;3)

Für k=4 ergeben sich foldende Vielkreissysteme:

(9;4) (11;4) (13;4) (15;4)

Für k=5 ergeben sich foldende Vielkreissysteme:

(11;5) (12;5) (13;5) (14;5) (16;5)

Für k=6 ergeben sich foldende Vielkreissysteme:

(13;6)

Für k=7 ergeben sich foldende Vielkreissysteme:

(15;7) (16;7)

Eine Zusammenfassung der ersten primären Systeme lässt sich hier finden: Primäre Vielkreis-Systeme

Lässt man zu das n und k nicht teilerfremd sind, so entstehen dadurch keine neuen Kreissysteme, sondern durch die Kürzungen bedingt, entstehen wieder primäre Systeme.

Eine Zusammenfassung der kompletten Systeme lässt sich hier finden: Vielkreis-Systeme komplett


Die primären Vielkreis-Systeme stellen quasi die Primzahlen der Brüche dar.