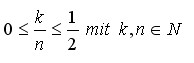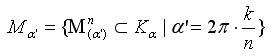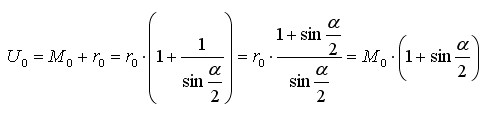0.1 - KOORDINATENSYSTEMUm ein Vielkreis-System zu erzeugen, bedarf es eines Koordinatensystems, dass als Grundlage für den Winkel alpha dient. In diesen Winkel legt man einen Kreis mit dem Radius r0.
Der Abstand des Kreismittelpunktes vom Koordinatenmittelpunkt, also die Strecke OM = M0 ist aus den gegebenen Daten berechenbar:
0.2 - VEKTORFasst man die Strecke OM = M0 als Vektor R auf, so ergeben sich die folgenden x,y-Komponenten:
0.3 - DREHUNGDreht man den Mittelpunktabstand mit dem Kreis jetzt noch um den Winkel alpha entgegen Uhrzeigersinn, dann lässt sich hier mathematisch eine Drehung formulieren. .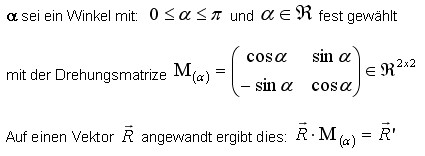
0.4 - DEFINITION: Menge der DrehungenKalpha ist die Menge aller Drehungen 0.5 - DEFINITION: Menge der Vielkreis-SystemeDreht man einen Kreis bzw. den zugehörigen Vektor n-mal und schließt sich die Kreisfigur nach k Umdrehungen wieder dann gilt:
Es gelte: k,n sind teilerfremd und:
0.6 - DEFINITION: UmkreisUm ein Vielkreis-System lässt sich noch ein Umreis legen:
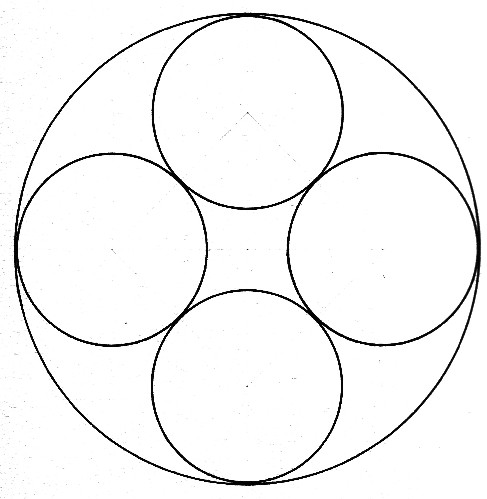
0.7 - BEISPIEL: 4 Keis-System
|