Logarithmische Spirale

Sonnenring am Bodensee

50 sakrale Stätten in einer Spiralanordnung

1.5.2 - Logarithmische Spirale 74 Orte

1.5.2.1 - Ansatz

Legt man die Werte für den Umlaufwinkel (aus der Abstandstabelle im Dokument „Ansatz Spirale“) als x-Achse fest und trägt den Logarithmus des Abstandes (von Heiden aus) als y-Werte auf so ergibt sich für alle 74 Punkte folgendes Diagramm

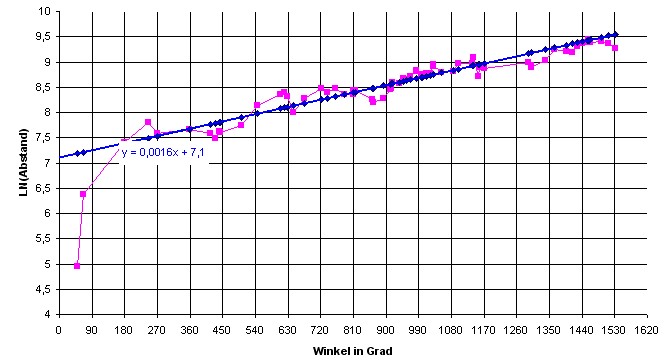Die blaue Linie ist einerseits die günstigste Gerade für alle Punkte, andererseits stellt sie auch den Verlauf einer logarithmische Spirale dar.

Mathematischer Ansatz für eine logarithmische / exponentielle Spirale

Die blaue Linie im ersten Diagramm ist einerseits die günstigste Gerade für alle Punkte, die ja Logarithmus des Abstandes sind, andererseits stellt sie auch den Verlauf einer logarithmische n Spirale dar.

Die Gerade im ersten Diagramm besitzt die Funktionsgleichung: ln y = 0,0016·φ + 7,1

In einem ersten Ansatz also: R(φ) = A·e^φ = e^{0,0016·φ + 7,1} = 1212·e^0,0016·φ

Was im folgenden Diagramm zu sehen ist:

1.5.2.2 - 1000 m - Betrachtung

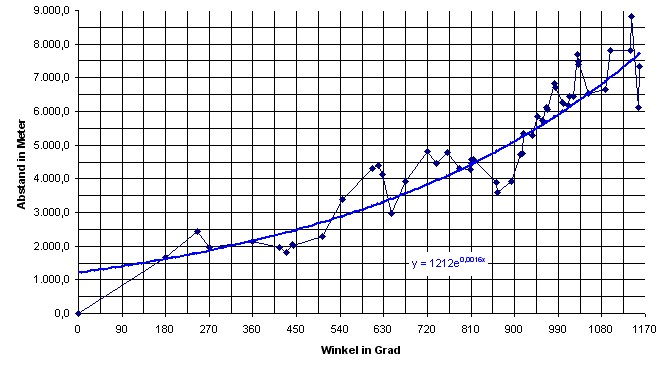Eine Methode den Punkteverlauf zu glätten, also einer Geraden anzupassen, besteht darin alle Punkte zu entfernen die eine zu starke Abweichung von der Geraden besitzen. In diesem Fall verbleiben nur Punkte die maximal 1 Km von der Spirallinie entfernt sind. Was im folgenden Diagramm zu sehen ist.

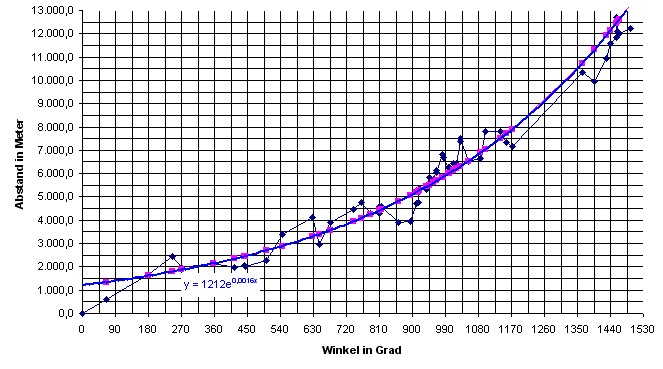Das Diagramm zeigt die Orte an, die sich auf , neben oder in der Nähe der Spirale befinden. Es sind die Punkte:
3,4,5,6,7,8,10,11,12,13,17,51,18,21,22,24,28,25,26,27,30,31,33,32,34,35,36,37,39,38,40,41,42,43,45,44
46,48,47,52,20,53,54,56,58,63,64,66,67,69,68,70,71,72

1.5.2.3 - 500 m - Betrachtung

Eine weitere Glättung kann erreicht werden wenn nur noch Punkte verbleiben die maximal 500 Meter von der Spirallinie entfernt sind. Was im folgenden Diagramm zu sehen ist.

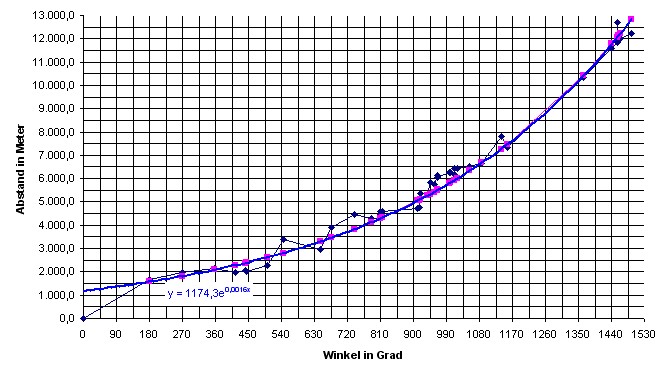Das Diagramm zeigt die Orte an, die sich auf , neben oder in der Nähe der Spirale befinden. Es sind die Punkte:
4,6,7,8,10,11,12,13,51,18,21,24,28,25,26,27,33,32,34,35,36,37,39,38,42,43,45,44,46,52,20,54,56,63,67
69,68,70,71,72

1.5.2.4 - 100 m - Betrachtung

Eine weitere Glättung kann erreicht werden wenn nur noch Punkte verbleiben die maximal 100 m von der Spirallinie entfernt sind. Was im folgenden Diagramm zu sehen ist

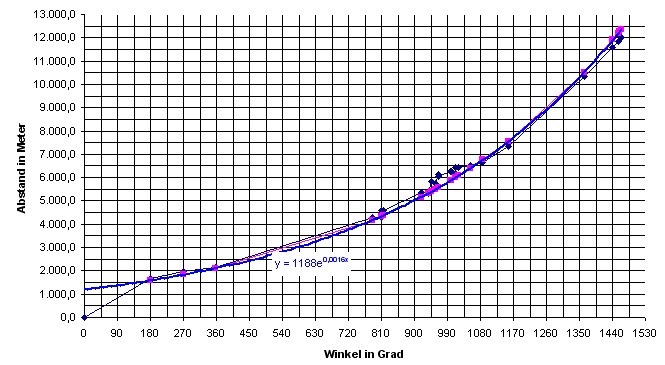Das Diagramm zeigt die Orte an, die sich auf , neben oder in der Nähe der Spirale befinden. Es sind die Punkte:
4,6,7,24,28,25,26,27,34,35,36,37,39,38,42,43,45,44,46,52,20,56,63,67,69,70,71

1.5.2.5 - Bilanz

Mit einer weiteren Glättung und Anpassung lässt sich dann dieses Ergebnis erzielen:

R(φ) = e^{0,0016·φ + 7,08} = 1188·e^0,0016·φ

bei Amazon kaufen

120 Seiten, davon 76 in Farbe
110 Bilder

Herstellung und Verlag:
Books on Demand GmbH, Norderstedt

ISBN 9783756215683

Ladenpreis: 17 Euro