Copyright © Klaus Piontzik
|
Aus der
Schule, und aus den Medien, kennen wir das Magnetfeld der
Erde stets als ein Feld, das dem Feld eines Stabmagneten
entspricht. Es ist das sogenannte Dipolfeld. Der physikalische Ansatz für ein solches Magnetfeld besteht in der Betrachtung des Magnetfeldes einer Leiterschleife. Die mathematische Ableitung führt zu einer Differentialgleichung, in der ein sogenanntes elliptisches Integral auftaucht, für das keine geschlossene mathematische Lösung - in Form einer Gleichung - existiert. |
|
| Abbildung 1.1 - Leiterschleife und Dipolfeld |
| Die allgemeine Vorgehensweise besteht darin, den auftretenden Term im Integral in eine unendliche Reihe umzuwandeln. |
Vereinfacht: |
| B = a1·x + a2·x2 + a3·x3 + a4·x4 + ... |
|
Dann geht man hin und schneidet diese Reihe nach dem ersten Glied einfach ab. Integriert man nun das Übriggebliebene, so entsteht die Gleichung für das Dipolfeld: |
 |
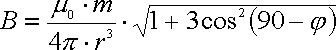| In der Gleichung steht B für die magnetische
Flussdichte, φ für die
geographische Breite, m
für das magnetische Moment, r
für den Erdradius und µ für die magnetische
Permeabilität. m, r, µ sind Konstanten die wie folgt definiert werden: Das magnetische Moment ist in diesem Fall das
magnetische Moment der Erde mit m = 6,6845*1022 Am2 Für den Erdradius nimmt man den Wert aus einem geodätischen System, in diesem Fall das WGS84, dass diesen angibt mit: r = 6378155 m Die magnetische Permeabilität µ = 10-7 Vs/Am (Zur Ableitung des Dipolfeldes siehe z.B. auch "Berkeley Physik Kurs 2" von Edward Purcell, Seite 266-269) |
| Es wird zwischen den
magnetischen Polen und den geomagnetischen Polen
unterschieden. Die magnetischen Pole sind die Orte an
denen das Magnetfeld senkrecht auf der Erdoberfläche
steht. Die geomagnetischen Pole sind die Pole des
Dipolfeldes. An den geomagnetischen Polen schneiden sich
die Achse des angenäherten Dipolfeldes und die
Erdoberfläche. Zuerst soll hier die Dipolachse, also die geomagnetischen Pole, betrachtet werden. In älteren Physikbüchern findet man häufig folgende Werte für die Dipolachse (Stand 1980): |
| Name | Breite |
Länge |
| Dipolachse - Nord | +78,8 Grad Nord | -70,9 Grad West |
| Dipolachse - Süd | -78,8 Grad Süd | +109,1 Grad Ost |
| Für die Dipolachse erhält man, in der populärwissenschaftlichen Literatur, auch die Koordinaten 79 Grad Nord in Breite und 70 Grad West in Länge. |
| Im Buch wird noch das Dipolmodell, dass auf dem IGRF 1995 beruht, behandelt. |
| Die Dipolachse ist also, im Vergleich zur physikalischen Rotationsachse, etwa um 11 Grad gekippt. Dieser Winkel muss in der obigen Gleichung noch berücksichtigt werden. Setzt man die Werte für die Konstanten ein, so ergibt sich folgende Endgleichung für die magnetische Flussdichte, die praktisch nur noch von der geographischen Breite abhängig ist: |
 |
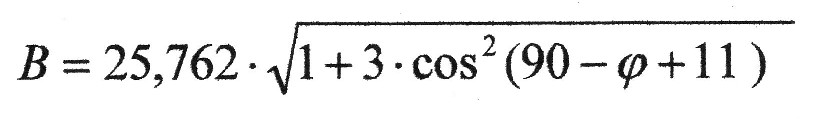µT (mükroTesla) |
| Bemerkung: 1 µT = 1000 γ (1 mükroTesla = 1000 Gamma) |
| Die hier
dargestellte mathematische Vorgehensweise zur Erreichung
der Dipolgleichung kann, aufgrund der abgeschnittenen
Restglieder, lediglich als eine erste Näherung
betrachtet werden.
Zumal im Buch noch zu sehen ist, dass das Dipolmodell im
Laufe der Zeit, in seiner räumlichen Position, nicht
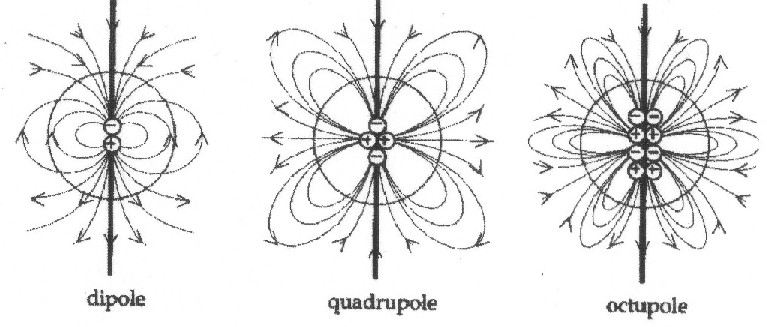
konstant ist und ständig angepasst werden muss. Fängt man an, die restlichen Glieder der unendlichen Reihe (aus der Leiterschleifenbetrachtung) zu integrieren, so erhält man das Quadrupolfeld, das Oktupolfeld usw. |
|
Abbildung 1.2 - Die Multipolentwicklung des Magnetfeldes |
|
Durch die Umwandlung des Terms in eine Reihe ist der
ganze Vorgang ein approximativer, die Lösung also nur
eine Näherung. Darüber hinaus ist stets zu bedenken,
dass die geschilderte Vorgehensweise eine rein
mathematische ist. Die Frage nach physikalischer Relevanz des Multipolmodells
bleibt dabei offen! Nimmt man tatsächliche Werte (Totalintensität) des Feldes, so lässt sich an den magnetischen Polen anschaulich zeigen, dass das Dipolmodell nicht genügt, um das Erdmagnetfeld hinreichend zu erklären. |
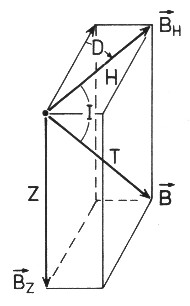
| Der Feldvektor B des Erdmagnetfeldes wird in der Regel durch drei voneinander unabhängige Zahlengrößen beschrieben, die als Elemente des magnetischen Erdfeldes bezeichnet werden. Es existieren zwei verschiedene Systeme der Darstellung. Der Einfachheit halber wird hier nur das System aus Abbildung 1.3 gezeigt und erläutert. |
|
| Abbildung 1.3 - Feldelemente des Erdmagnetfeldes |
|
Der horizontale Winkel zwischen der Richtung vom
magnetischen zum geographischen Nordpol wird als Deklination D
oder auch als Missweisung bezeichnet. Die horizontale
Richtung zu den magnetischen Polen lässt sich
unmittelbar mit einem Kompass bestimmen. Für die vertikale Abweichung des Magnetfeldvektors von der Parallelorientierung zur Erdoberfläche wird der Begriff Inklination I verwendet. Wenn man den Kompass so verdreht, dass seine Achse horizontal liegt, haben wir ein Inklinatorium vor uns - es misst den Winkel zwischen der Erdoberfläche und dem Magnetfeld. Das es diesen Winkel gibt und das er vom Messort abhängt ist seit über 400 Jahren bekannt. Der Fakt, dass am Pol das Magnetfeld senkrecht auf der Erdoberfläche steht, am Äquator aber parallel zu ihr, hat ja mit zum Dipolmodell geführt. Die vertikale Komponente des Magnetfeldvektors wird Vertikalintensität Z genannt. (siehe auch "Grundlagen der Geophysik" von Hans Berckhemer, S.138) |
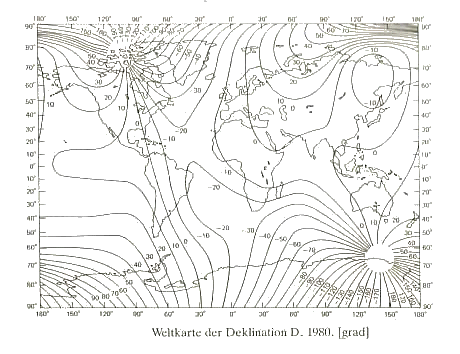
| Nimmt man das International Geomagnetic Reference Field (kurz IGRF) von 1980 für die Deklination so ergibt sich die folgende Abbildung 1.4. (zum IGRF siehe auch Kapitel 2.2) |
 |
Durch
Auswertung der Deklination, also der waagerechten
Fehlweisung des Erdfeldes, lassen sich zwei Bereiche
gewinnen. Nämlich der süd- und der nordmagnetische Pol,
d. h. die Orte an denen das Magnetfeld quasi nur
senkrecht auf der Erdoberfläche steht und daher hier
keine waagerechte Fehlweisung vorhanden ist. Diese beiden
Bereiche definieren die magnetischen Pole. Alternativ zur Deklination lässt sich natürlich auch die Inklination zur Polbestimmung heranziehen. |
|
| Abbildung 1.4 - Die Deklination des Erdmagnetfeldes - IGRF 1980 |
| Die Koordinaten der eigentlichen Pole lassen sich bestimmen, indem man die Ränder der Polgebiete aus Abb. 1.4 ermittelt und daraus die Mittelwerte bildet: |
Name |
Breite | Länge |
| Südmagnetischer Pol | +75 Grad Nord | -103,5 Grad West |
| Nordmagnetischer Pol | -65,5 Grad Süd | +141 Grad Ost |
| In Physikbüchern oder in der populärwissenschaftlichen Literatur findet man aber auch die folgenden Koordinaten: |
Name |
Breite | Länge |
| Südmagnetischer Pol | +75 Grad Nord | -101 Grad West |
| Nordmagnetischer Pol | -67 Grad Süd | +143 Grad Ost |
| Fasst man beide Ergebnisse zusammen, ergeben sich die Bereiche, in denen die magnetischen Pole heutzutage liegen: |
Name |
Breite | Länge |
| Südmagnetischer Pol | 75 Grad Nord | 101-103,5 Grad West |
| Nordmagnetischer Pol | 65,5-67 Grad Süd | 141-143 Grad Ost |
| Im Buch werden noch die geltenden Polbereiche für 2005 behandelt. |
|
Vergleicht man die gefundenen Bereiche,
aus Kapitel 1.4 mit den Koordinaten der Dipolachse aus
Kapitel 1.2, erkennt man:
1) Die Polbereiche liegen sich nicht gegenüber, wie man es nach der Dipoltheorie erwarten würde. 2) Die vorhandenen Polbereiche liegen noch nicht einmal in der Nähe der Dipolachse. |
|
Daraus lassen sich zwei mögliche
Schlüsse ziehen: 1) das hier weitere Einflüsse vorliegen müssen, die das Dipolfeld stören bzw. verzerren. Das Dipolmodell stellt somit nur eine Teilansicht des gesamten erdmagnetischen Feldes dar. Die starke räumliche Änderung der Dipolachse im Laufe der Zeit spricht ebenfalls dafür. 2) das Dipolmodell passt hier nicht und man nach einem neuen Ansatz Ausschau halten müsste. Das Dipolmodell langt auch nicht um das, im nächsten Kapitel behandelte, magnetische Gesamtfeld der Erde mit seinen vier Extremas zu beschreiben oder zu erklären. Das Fazit ist: |
| Das Dipolmodell allein reicht
nicht aus, um das tatsächliche Erdfeld erklären zu können . |
| Und bei der Multipolentwicklung des Erdfeldes bleibt
die Frage nach physikalischer Relevanz offen !!! Bemerkung: Schon Gauß und Weber erkannten 1838, durch ihre Versuche mit dem Erdmagnetfeld, dass das Magnetfeld nicht einfach durch das Modell eines Stabmagneten bzw. einer Leiterschleife erklärt werden kann. (siehe dazu auch Kapitel 2.7) |
| Das Buch zur Website - Die Website zum Buch | ||
|
In 1000 Online Shops und
überall im Buchhandel
|
| Das weiterführende Buch: Planetare Systeme der Erde |
| Die Theorie, die in diesem Buch entwickelt wird, basiert auf der Neuauflage und Erweiterung einer alten Idee. Es handelte sich um die Idee eines Zentralkörpers, vorzugsweise in Kugelgestalt, um den herum und/oder in dem sich konzentrische Schichtungen gebildet haben.
Demokrit war der erste der diese Idee mit seiner Atomtheorie vertrat und sich dabei die Atome als feste und massive Bausteine vorstellte.
Wird für das Atom ein Wellenmodell zugrunde gelegt, dass es gestattet konzentrische Schichtungen als Ausdruck eines räumlichen radialen Oszillators zu interpretieren, so gelangt man zum derzeit geltenden Orbitalmodell der Atome. In diesem Buch wird nun gezeigt, dass diese oszillatorischen Ordnungsstrukturen auch auf die Erde und ihre Schichtungen (geologisch und atmosphärisch) umsetzbar sind. Darüber hinaus lässt sich die Theorie auch auf konzentrische Systeme anwenden, die nicht kugelförmig sondern flächig sind, wie das Sonnensystem mit seinen Planetenbahnen, den Ringen die manche Planeten besitzen und die Monde von Planeten oder auch die Nachbargalaxien der Milchstrasse. Auch auf Früchte und Blumen ist dieses Prinzip anwendbar, wie Pfirsich, Orange, Kokosnuss, Dahlie oder Narzisse. Das lässt den Schluss zu, dass die Theorie eines Zentralkörpers als räumlicher radialer Oszillator auch auf andere kugelförmige Phänomene angewendet werden kann, wie z.B. kugelförmige galaktische Nebel, schwarze Löcher oder sogar das Universum selber. Das wiederum legt die Vermutung nahe, dass die Idee des Zentralkörpers als räumlicher radialer Oszillator ein allgemeines Prinzip der Strukturgebung in diesem Universum darstellt, sowohl makroskopisch, als auch mikroskopisch und submikroskopisch. |
|
