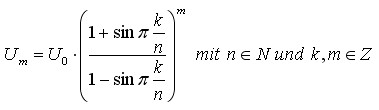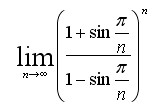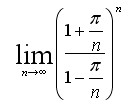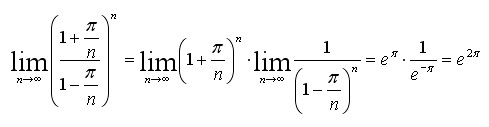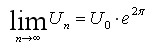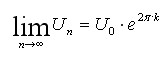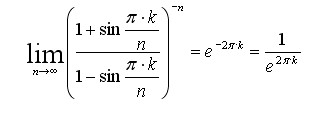| Die allgemeine Gleichung
für die Umkreise von Vielkreis-Systemen lautet:
Man kann erstmal k=1 setzen ohne die folgenden Betrachtungen einzuschränken. Setzt man m=n und lässt n dann gegen unendlich gehen, d.h. man lässt die Vielkreis-Systeme unendlich wachsen und erhöht gleichzeitig die Anzahl der Kreise auf unendlich. Dennoch strebt die Gleichung einem endlichen Grenzwert entgegen. Zu untersuchen ist folgender Term:
Für große n wird der Winkel sehr klein und man kann die Winkelfunktion direkt durch die Argumente ersetzen:
Dann ergibt sich insgesamt:
Damit gilt allgemein:
Nimmt man jetzt noch die Variable k wieder hinzu, ergibt sich folgendes Ergebnis:
Da der Exponent m Element der ganzem Zahlen ist, kann m auch negativ werden. Es findet also kein Wachstum sondern eine Verkleinerung statt. Der zugehörige Grenzwert ergibt sich dann zu:
|