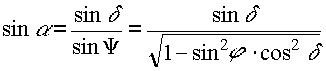|
Mittlerweile kann man exakt berechnen, zu welcher Zeit und an
welchem Ort eine Sonnenfinsternis eintreten wird. Wer schon einmal
ein solches Ereignis miterlebt hat, weiß um die spürbare Faszination,
wenn der Mond die Sonne verdunkelt. So interessant eine Sonnenfinsternis ist,
sollte man aber auch bei einem so beeindruckenden Naturschauspiel nicht leichtsinnig
werden und die Augen niemals ungeschützt den Sonnenstrahlen aussetzen.
Zu wissen ist hierbei, dass eine herkömmliche Herren- oder Damen Sonnenbrille bei einer Sonnenfinsternis nicht ausreicht. Man sollte seine Augen auf jeden Fall mit einer speziellen Sonnen-Sicht-Brille schützen, um keinen zeitweisen oder sogar dauerhaften Sehverlust durch Verbrennungen zu riskieren. Und das gilt grundsätzlich für Sonnenstrahlen, nicht nur bei einer Sonnenfinsternis. Wer im Sommer gerne und viel draußen ist und dadurch seine Haut der Sonne aussetzt, muss sich dementsprechend schützen. Zum Schutz zählt leichte Sommerkleidung, aber auch eine normale Sonnenbrille, zudem ist eine Sonnencreme mit hohem Schutzfaktor empfehlenswert. Wer eine sonnenbeschienene Terrasse besitzt, kann mit Sonnenschirm oder Markisen arbeiten. Solche Fachgeschäfte vor Ort findet man leicht, indem man beispielsweise nach „ Markisen München“ sucht. Doch zurück zur Sonnenfinsternis. Das folgende Bild zeigt die scheinbare (Tages) Bahn der Sonne an der Himmelskugel. Von einem beliebigen Ort (der nördlichen Hemisphäre) der Erde aus betrachtet. Dargestellt sind vier Zeitpunkte bzw. vier Tage: |
||
| Sonnenbahn am 21.3 und 21.9 | Tag- und Nachtgleiche | |
| Sonnenbahn am 21.6 | Sommersonnenwende | |
| Sonnenbahn am 21.12 | Wintersonnenwende | |
| Der Punkt M
stellt den eigenen Standort dar, Z
ist der Zenit und P der Himmelspol Ost und West sind die Auf- bzw. Untergangspunkt zur Tag- und Nachtgleiche A und D sind Auf- bzw. Untergangspunkt zur Sommersonnenwende B und C sind Auf- bzw. Untergangspunkt zur Wintersonnenwende |
||
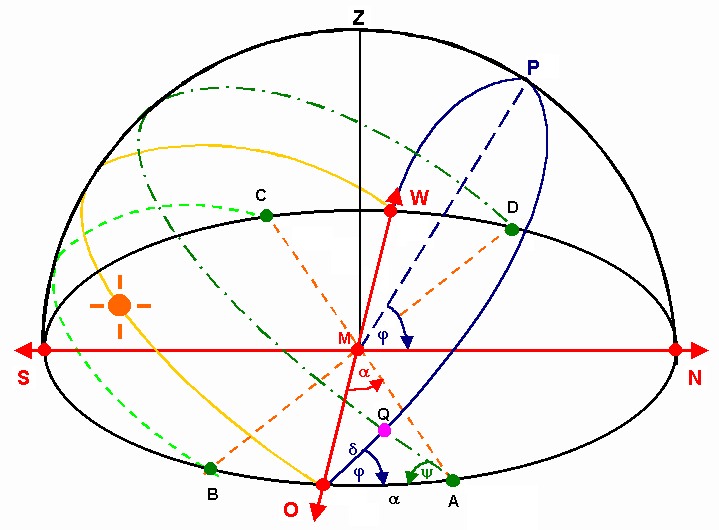
| Zu bestimmen ist nun der Winkel α, das ist die Abweichung der Punkte A,B,C,D von der Ost-West-Richtung. | ||
 |
||
| φ: geographischen Breite | ||
| δ: Neigung der Ekliptik - 23 Grad 27 Minuten | ||
| α: Abweichung von der Ost-West-Richtung | ||
| Für das Dreieck AQO (rechter Winkel in Q) gilt nach dem Sinus-Satz der sphärischen Trigonometrie: | ||
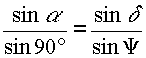 |
||
| ==> | 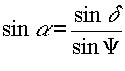 |
|
| Die Zwischengrösse ψ muss jetzt noch berechnet werden. Nach dem Cosinus-Satz der sphärischen Trigonometrie gilt für das Dreieck AQO : | ||
| Es gilt: | ||
| ==> | ||
| cos ψ lässt sich über den Satz des Pythagoras in eine Sinusfunktion umformen: | ||
| Einsetzen des Terms für sin ψ in die obige Gleichung für sin α ergibt: | ||