M sei ein beliebiger Messbereich mit:
MMax = Maximum Messbereich
MMin = Minimum Messbereich
Die Messpunkte (als Zahlenfolge) und damit der Messbereich werden in äquivalente natürliche Zahlen p abgebildet. Jedem Messpunkt wird dabei ein bestimmter eindeutiger Zahlenwert p zugeordnet. n bestimmt dabei die Auflösung.
Für n=64 ist eine direkte weitere Behandlung mit den hier beschriebenen Farb- und Tonalgorithmen möglich. Die Farb- und Tonalgorithmen sind so ausgelegt das die Möglichkeit für ein variables n bereits darin enthalten sind, so dass auch größere Auflösungen als eine 64 Punkte Skala möglich sind.
Verallgemeinerung der spektralen Farbzuordnung
Der Farbalgorithmus 1 ist so ausgelegt das die Möglichkeit für ein variables n bereits darin enthalten ist, so dass auch größere Auflösungen als eine 64 Punkte Skala möglich sind. Es gilt allgemein:LMax = blaues Ende des sichtbaren Spektrums
LMin = rotes Ende des sichtbaren Spektrums
Die Messpunkte des vorgegebenen Messbereichs bzw. die zugehörigen Positionswerte p werden auf Farben (Wellenlängen) des sichtbaren Spektrums linear und damit auch äquivalent abgebildet.
Da LMax und LMin frei wählbar sind steht damit auch eine Funktion zur Verfügung die Messpunkte auf beliebige Bereiche des elektromagnetischen Spektrums zu übertragen.
So lassen sich auch beliebige Messbereiche (z.B. EEG, EKG, Blutdruck, Temperatur) in Farben oder in beliebige Bereiche des elektromagnetischen Spektrums äquivalent übertragen.
Verallgemeinerung der Tonzuordnung
Auch der Tonalgorithmus 1 ist so ausgelegt das die Möglichkeit für ein variables n bereits darin enthalten ist, so dass auch größere Auflösungen als eine 64 Punkte Skala möglich sind. Es gilt allgemein:Die Messpunkte des vorgegebenen Messbereichs bzw. die zugehörigen Positionswerte p werden auf Töne (Frequenzen) des hörbaren Spektrums linear und damit auch äquivalent abgebildet.
Da fMax und fMin frei wählbar sind steht damit auch eine Funktion zur Verfügung die Messpunkte auf beliebige Bereiche des Schallspektrums zu übertragen.
Gleiches gilt für die Funktionale Zuordnung (Ton-Algorithmus 1.1) die einen gleichabständigen Aufbau einer Tonleiter ermöglicht, wie z.B. bei der Naturtonfolge oder der Obertonfolge.
Gleiches gilt für die Gleichstufige Zuordnung (Ton-Algorithmus 2) die Tonleiter ermöglicht wie beim 12-Tonsystem oder 19-Tonsystem.
Gleiches gilt für eine beliebige Tonleiter deren Töne aufsteigend geordnetend sind. (Ton-Algorithmus 3)
Insgesamt ist durch die vorhandenen Tonalgorithmen gewährleistet, dass eine lineare (sogar isomorphe, also eineindeutige) Abbildung zwischen Messbereich und Tönen vorhanden ist.
So lassen sich auch beliebige Messbereiche (z.B. EEG, EKG, Blutdruck, Temperatur) in Töne oder in beliebige Bereiche des Schallspektrums äquivalent übertragen.
Verallgemeinertes Verfahren
Statt Tripletts kann man auch beliebige Messbereiche (z.B. EEG, EKG, Blutdruck, Temperatur) durch eine entsprechende Linearisierung so transformieren, dass eine weitere Behandlung mit den hier beschriebenen Farb- und Tonalgorithmen möglich ist.Das Bild zeigt das Gesamtschema der Konvertierung eines beliebigen Messbereiches (in Form einer Datenliste) in Farben und Töne.
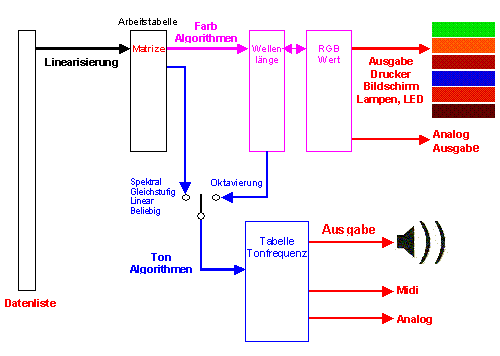
Durch den Farb-Algorithmus 1 (Spektrale Farbzuordnung) und den Ton-Algorithmen 1 (Spektrale Tonzuordnung), 2 (Gleichstufige Tonzuordnung), 3 (Lineare Tonzuordnung) und 4 (Oktavierung) ist gewährleistet, dass eine lineare (sogar isomorphe, also eineindeutige) Abbildung zwischen dem abzubildenden Messbereich und Farben wie Tönen vorhanden ist.
Die erzeugten Farben und Töne können daher als reale Entsprechung dieses Messbereiches auf akustische und optische Wahrnehmungsebenen aufgefasst werden.
Das hier geschilderte Konvertierungsverfahren Informationen in Farben und Töne zu übertragen, samt aller darin geschilderten Algorithmen, ist durch Computer bzw. Mikrocomputer, Mikroprozessorsysteme oder Mikrocontroller oder Computerprogramme generierbar, aber auch durch elektrische, elektronische oder digitale Schaltungen sowie durch physikalische, biologische oder chemische Vorrichtungen abbildbar und realisierbar.
Die Algorithmen sind so ausgelegt das eine Konvertierung eines Messbereiches in alle Schallbereiche (Infraschall, Ultraschall) sowie über das gesamte elektromagnetische Spektrum hinweg möglich ist. Ebenso ist eine Konvertierung und Umsetzung als rein elektrische oder magnetische oder elektromagnetische Felder realisierbar, oder auch als elektrische Spannungen und Ströme.
Ebenso möglich ist eine Kalibrierung der Konvertierung auf Frequenzspektren die auf sogenannten biologischen Frequenzen basieren, wie die Schumannfrequenz, die Erdfrequenz, die Sferics oder die Frequenzen des Adey-Fensters.
